3.6. Спектр колебания при гармонической угловой модуляции

Используем полученные выше результаты для анализа колебания вида

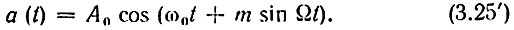
Это выражение совпадает с (3.23) и (3.23') при модуляции частоты по закону ω(t) = ω₀ + ω_д cos Ωt. Начальная фаза θ₀, а также начальная фаза модулирующей функции γ опущены для упрощения выкладок. В случае необходимости они легко могут быть введены в окончательные выражения.

В данном случае θ(t) = m sin Ωt. Подставляя θ(t) в выражение (3.26), получаем

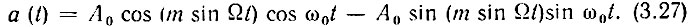
Учитывая, что множители cos (m sin Ωt) и sin (m sin Ωt) являются периодическими функциями времени, разложим их в ряд Фурье.

В теории бесселевых функций доказываются следующие соотношения:

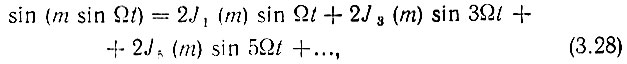
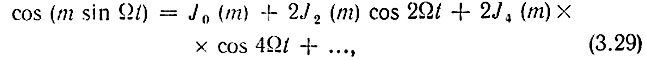
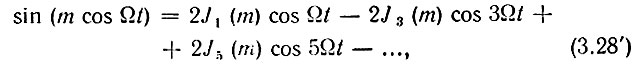
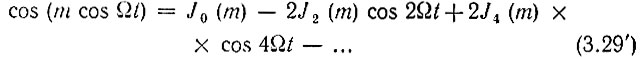
Здесь J_n(m) - бесселева функция первого рода n-го порядка от аргумента m.

С помощью соотношений (3.28) и (3.29) уравнение (3.27) можно привести к виду

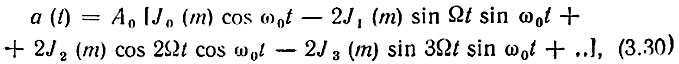
или в более развернутой форме

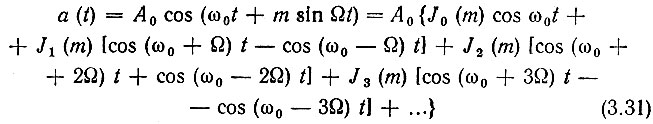
Таким образом, при частотной и фазовой модуляции спектр колебания состоит из бесконечного числа боковых частот, расположенных попарно симметрично относительно несущей частоты ω₀ и отличающихся от последней на nΩ, где n - любое целое число. Амплитуда n-й боковой составляющей равна А_n = J_n(m) A₀, где А₀ - амплитуда немодулированного колебания, а m - индекс модуляции. Отсюда следует, что удельный вес различных боковых частот определяется величиной m.

Рассмотрим режимы угловой модуляции при малых и больших значениях m. Если m << 1, так что имеют место приближенные равенства

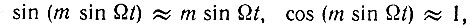
то выражение (3.27) переходит в следующее:

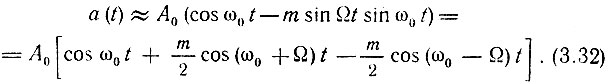
Сравним это уравнение с уравнением для амплитудно-модулированного колебания, у которого модулирующая функция (т. е. передаваемое сообщение) такая же, как и при частотной модуляции. Так как выражение (3.32) получено из (3.25') для модуляции частоты по закону ω(t) = ω₀ + ω_д cos Ωt, то для удобства сравнения зададим модуляцию амплитуды по аналогичному закону A(t) = A₀ (1 + М cos Ωt). Тогда амплитудно-модулированное колебание запишется в форме

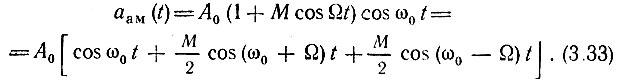
Из сравнения (3.32) и (3.33) видно, что при малых значениях m спектр колебания, как и в случае амплитудной модуляции, состоит из несущей частоты ω₀ и двух боковых частот: верхней ω₀ + Ω и нижней ω₀ - Ω. Единственное отличие заключается в фазировке колебаний боковых частот относительно несущего колебания. При AM фазы колебаний боковых частот симметричны относительно несущей частоты, а при угловой модуляции фаза колебания нижней боковой частоты сдвинута на 180° [знак минус перед последним слагаемым в (3.32)]. Это положение иллюстрируется векторной диаграммой, показанной на рис. 3.15, а. Направление вектора DC₂ при амплитудной модуляции обозначено штриховой линией. Изменение направления этого вектора на 180° приводит к тому, что вектор модуляции DF всегда перпендикулярен к направлению вектора OD, изображающего несущее колебание (рис. 3.16, а). Вектор OF, изображающий результирующее колебание, изменяется как по фазе, так и по амплитуде; однако при m = θ_макс << 1 амплитудные изменения настолько малы, что ими можно пренебрегать и модуляцию можно в первом приближении рассматривать как чисто фазовую.

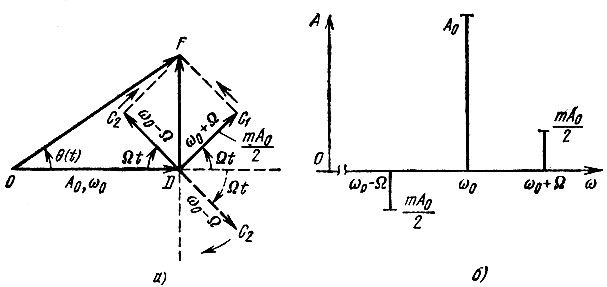
Рис. 3.15. Векторная диаграмма (а) и спектр колебания (б) при угловой модуляции с индексом m < 1

Спектральная диаграмма угловой модуляции при m << 1 показана на рис. 3.15, б. Симметрия амплитуд колебаний боковых частот сохраняется, а фаза колебания нижней частоты сдвинута на 180°. Амплитуды колебаний боковых частот равны mА₀/2 и поэтому в данном случае индекс модуляции m совпадает по величине с коэффициентом М, характеризующим глубину изменения амплитуды при амплитудной модуляции. Заметим, что ширина спектра при m << 1 равна 2Ω, как и при AM. Этот результат показывает, что при очень малых девиациях ω_д (по сравнению с Ω) ширина спектра от величины ω_д не зависит.

При увеличении фазового отклонения, т. е. при возрастании величины m, уравнение (3.32) и диаграмма на рис. 3.15, а не дают правильного представления о действительной картине явлений при частотной или фазовой модуляции. Это объясняется тем, что с помощью колебаний несущей частоты и всего лишь одной пары боковых частот невозможно представить колебание, частота или фаза которого изменяются в широких пределах, а амплитуда остается строго постоянной. Для получения правильной картины необходимо учитывать боковые частоты высших порядков в соответствии с выражением (3.31).

При значениях индексов m от 0,5 до 1 приобретает некоторое значение вторая пара боковых частот, ввиду чего ширина спектра должна быть приравнена 4Ω. Далее, при 1 < m < 2 приходится учитывать третью и четвертую пары боковых частот и т. д. Спектрограммы для m = 1 и m = 2 приведены на рис. 3.16. Фазы колебаний на этих рисунках не учитываются, однако следует иметь в виду, что при четных n симметрия фаз сохраняется, а при нечетных п амплитуды нижних боковых частот следует брать со знаком минус. Амплитуды всех составляющих спектра представлены на этих рисунках в виде вертикальных отрезков, длины которых равны J_n(m), а расстояния от отрезка J₀(m), соответствующего амплитуде колебания несущей частоты, равны nΩ, где Ω - частота модуляции, а n - порядковый номер боковой частоты. Амплитуда результирующего колебания принята за 100%, т. е. А₀ = 1; обозначенные на рисунках величины J_n(m) дают амплитуды колебаний соответствующих частот в долях от амплитуды результирующего колебания.

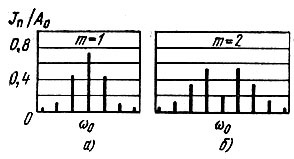
Рис. 3.16. Спектры колебания при угловой модуляции: а - при m = 1; б - при m = 2

Векторные диаграммы для моментов Ωt = 0, π/2, π и 3π/2 при m = 1, построенные по выражению (3.30), представленные на рис. 3.17, а, б, в и г.

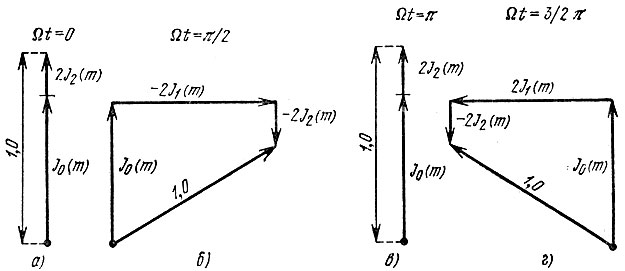
Рис. 3.17. Фазировка колебаний боковых частот в различные моменты времени

Рассмотрим теперь случай больших значений m. Вопрос сводится к выяснению зависимости бесселевой функции J_n(m) от порядкового номера n при больших значениях аргумента m. Оказывается, что при m >> 1 величина |J_n(m)| более или менее равномерна при всех целых значениях |n|, меньших, чем аргумент m. При |n|, близких к m, |J_n(m)| образует всплеск, а при дальнейшем увеличении |n| функция |J_n(m)| быстро убывает до нуля. Общий характер этой зависимости показан на рис. 3.18 для m = 100. Из рисунка видно, что наивысший номер n боковой частоты, которую еще необходимо принимать в расчет, приблизительно равен индексу модуляции m (в данном случае n = 100).

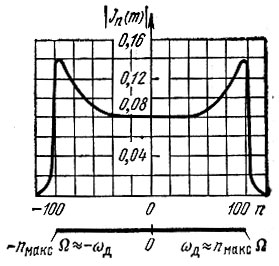
Рис. 3.18. Ширина спектра ЧМ колебания при больших значениях индекса модуляции m

Приравнивая это максимальное значение n_макс величине m, приходим к выводу, что полная ширина спектра модулированного колебания равна

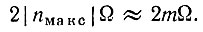
Но m = ω_д/Ω, следовательно, при больших индексах модуляции ширина спектра модулированного колебания близка девиации частоты

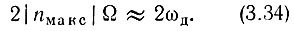
Эта полоса частот обозначена в нижней части рис. 3.18.

Заметим, что в соответствии с определением m [см. (3.24)], выражение "модуляция с малым индексом" эквивалентно выражению "быстрая модуляция", а выражение "модуляция с большим индексом" эквивалентна выражению "медленная модуляция". Поэтому можно сформулировать следующее положение: при быстрой угловой модуляции (когда ω_д << Ω) ширина спектра модулированного колебания близка к величине 2Ω; при медленной угловой модуляции (когда (ω_д >> Ω) ширина спектра близка к величине 2ω_д.