
3.7. Спектр радиоимпульса с частотно-модулированным заполнением
При модуляции частоты колебания по закону, отличающемуся от гармонического, нахождение спектра колебания усложняется. Выбор наиболее удобного метода анализа зависит от характера модулирующей функции. Поясним один из возможных методов на примере широко распространенного сигнала, так называемого ЛЧМ импульса, т. е. импульса с линейной частотной модуляцией. Подобный сигнал изображен на рис. 3.19, а, а закон изменения частоты заполнения импульса - на рис. 3.19, б.
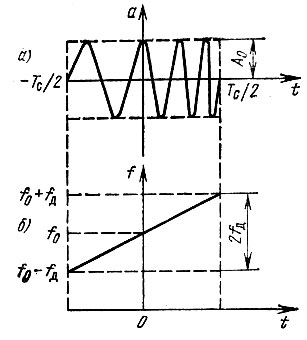
Рис. 3.19. ЛЧМ импульс (а) и изменение частоты его заполнения (б)
Мгновенную частоту заполнения 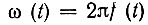 можно определить выражением
можно определить выражением
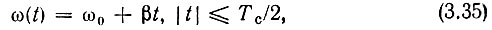
где
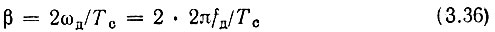
есть скорость линейного изменения частоты внутри импульса. Тогда мгновенное значение колебания, представленного на рис. 3.19, а, можно записать в виде
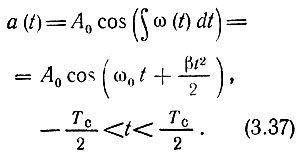
Произведение полной девиации частоты на длительность импульса

является основным параметром ЛЧМ сигнала. Сопоставление выражения (3.38) с (2.126) указывает на возможность трактовки m как базы ЛЧМ сигнала.
С учетом (3.38) выражение (3.36) можно записать в форме

При этом сигнал а(t) определяется выражением
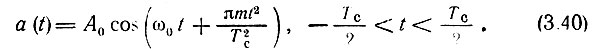
Определим спектральную плотность этого сигнала с помощью общего выражения (2.48):
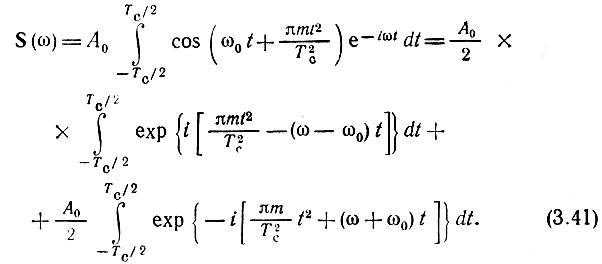
Первое слагаемое в правой части полученного выражения определяет всплеск спектральной плотности вблизи частоты ω = ω0, а второе - вблизи частоты ω = -ω0.
При определении S(ω) в области положительных частот второе слагаемое можно отбросить [см. формулу (3.10)]. В первом же слагаемом показатель степени в подынтегральной функции целесообразно дополнить до квадрата разности (β считаем положительной величиной)
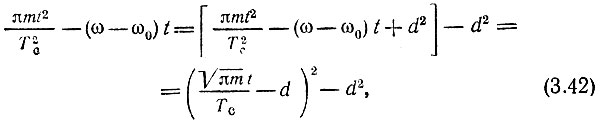
где
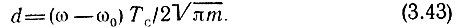
Подставляя выражение (3.42) в (3.41) и переходя к новой переменной

получаем
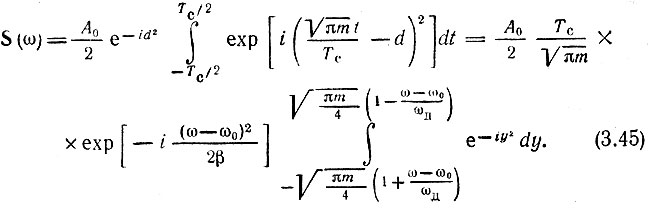
Введем следующие обозначения:
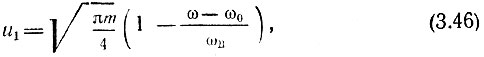
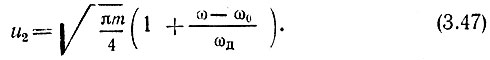
В этих обозначениях выражение S(ω) принимает следующий вид:
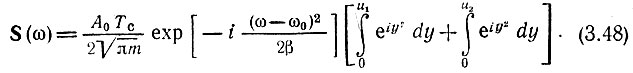
Используем известное из математики соотношение
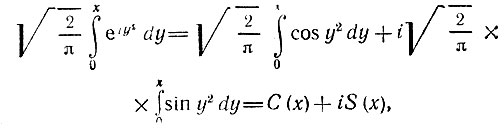
где C(x) и S(x) - интегралы Френеля.
С помощью этого соотношения выражение (3.48) можно привести к виду
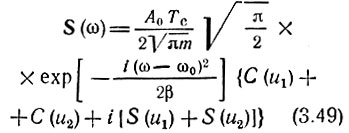
Из (3.49) следует, что модуль спектральной плотности рассматриваемого сигнала равен
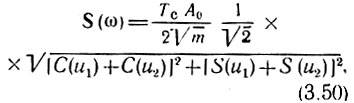
а фазовая характеристика спектра при ω > 0
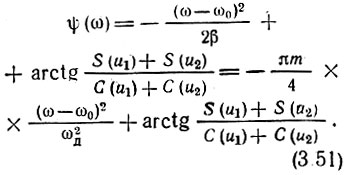
Графики зависимости 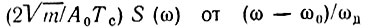 (рис. 3.20, а, б и в) показывают, что при больших значениях m форма S(ω) приближается к прямоугольной и ширина спектра близка к величине 2ωд. При этом фазовая характеристика |ψ(ω)| принимает вид квадратичной параболы (рис. 3.20, в). Второе слагаемое в (3.51), стремящееся к постоянной величине π/4, опущено.
(рис. 3.20, а, б и в) показывают, что при больших значениях m форма S(ω) приближается к прямоугольной и ширина спектра близка к величине 2ωд. При этом фазовая характеристика |ψ(ω)| принимает вид квадратичной параболы (рис. 3.20, в). Второе слагаемое в (3.51), стремящееся к постоянной величине π/4, опущено.
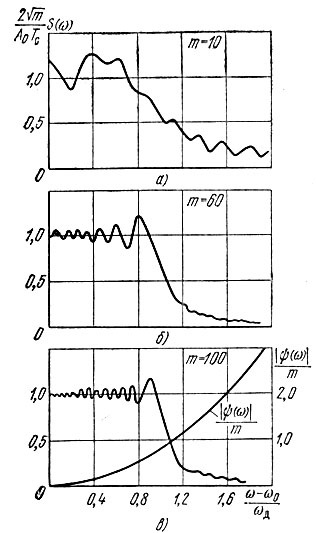
Рис. 3.20. Спектральная плотность ЛЧМ импульса при различных значениях базы m = 2fдTc
При 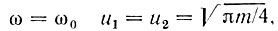 так что при больших значениях m и ω = ω0, когда
так что при больших значениях m и ω = ω0, когда
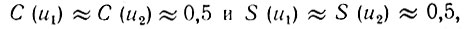
квадратный корень в выражении (3.50) обращается в 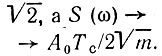

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
