3.8. Спектр колебания при смешанной амплитудно-частотной модуляции

Обобщим выражения (3.25), (3.26), заменив в них постоянную амплитуду А₀ функцией времени A(t):

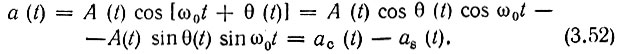
Как и в § 3.5, 3.6, определение спектра сводится к нахождению спектров функций А_с(t) = A(t) cos θ(t) и А_s(t) = A(t) sin θ(t), т. е. огибающих квадратурных колебаний, и к последующему сдвигу этих спектров на величину ω₀.

Обозначим спектральные плотности функций А_с(t) и A_s(t) символами S_AC(ω) и S_AS(ω). Тогда

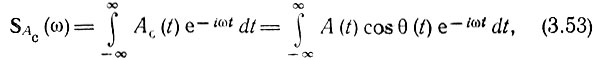
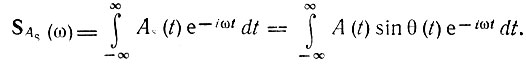
Спектральная плотность квадратурного колебания а_с(t) = А_с(t) cos ω₀t в соответствии с выражением (2.58) (при θ₀ = 0) будет

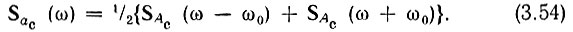
При определении спектра синусного квадратурного колебания фазовый угол θ₀ в (2.58) следует приравнять -90°. Следовательно,

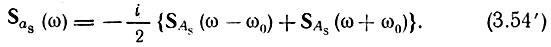
В области положительных частот можно считать

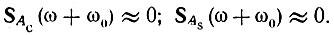
Таким образом, окончательно спектральная плотность колебания а(t) = а_с(t) - а_s(t) определяется выражением

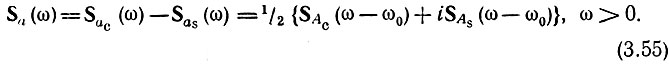
Переходя к переменной Ω = ω - ω₀, получаем

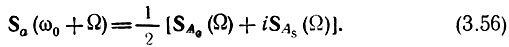
Структура спектра колебания а(t) при смешанной амплитудно-частотной модуляции зависит от соотношения и вида функций А(t) и θ(t).

При чисто амплитудной модуляции спектр колебания a(t) характеризуется полной симметрией амплитуд и фаз колебаний боковых частот относительно несущего колебания; при чисто угловой модуляции [A(t) = А₀ = const] симметричны только амплитуды, фазы же колебаний боковых частот ω₀ ± nΩ при нечетных n несимметричны относительно частоты ω₀ (см. § 3.6). Одновременная модуляция по амплитуде и углу может при некоторых соотношениях между A(t) и θ(t) приводить к асимметрии спектра S_a(ω₀ + Ω) относительно ω₀ не только по фазам, но и по амплитудам. В частности, если θ(t) является нечетной функцией t, то при любой функции А(t) спектр колебания a(t) несимметричен.

Действительно, пусть A(t) - четная функция. Тогда произведение A(t) cos θ(t) = A_с(t) - четная, а A(t) sin θ(t) = A_s(t) - нечетная функция t, и в соответствии со свойствами преобразования Фурье, перечисленными в § 2.7, п. 6, функция 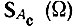является вещественной и четной относительно Ω, а 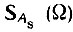- мнимой и нечетной. С учетом множителя i второе слагаемое в (3.56) становится также вещественной, но нечетной функцией Ω и, следовательно, спектральная плотность S_a(ω) оказывается вещественной функцией, несимметричной относительно точки ω = ω₀. Пример подобного спектра представлен на рис. 3.21. (По отношению к точке ω = 0 модуль спектральной плотности симметричен при любых условиях.)

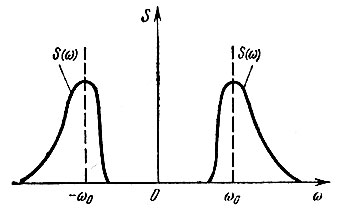
Рис. 3.21. Пример асимметричного спектра при смешанной амплитудной и частотной модуляции

Аналогичный результат получается и при нечетной функции А(t). В этом случае 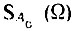- нечетная, мнимая функция Ω, а 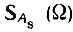- четная вещественная функция. Слагаемое 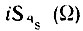в выражении (3.56) становится мнимым, и сумма 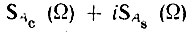становится функцией несимметричной (по модулю) относительно точки ω = ω₀.

С помощью аналогичных рассуждений нетрудно показать, что для симметрии спектра S_a(ω) требуется четность функции θ(t) при одновременном условии, чтобы функция А(t) была либо четной, либо нечетной функцией t. Если функция А(t) может быть представлена в виде суммы четной и нечетной составляющих, то спектр S_a(ω) несимметричен даже при четной функции θ(t). Например, импульс с линейной частотной модуляцией, рассмотренный в § 3.7, имеет симметричный спектр. В этом случае прямоугольная огибающая при надлежащем выборе точки отсчета времени является функцией, четной относительно t, как и функция θ(t) = ¹/₂βt².

Наглядное представление о деформации спектра колебания при двойной модуляции - амплитудной и угловой - можно получить, рассмотрев случай, когда оба вида модуляции осуществляются одной и той же модулирующей функцией. Для упрощения анализа зададим эту функцию в виде гармонического колебания cos Ωt для угловой модуляции и в виде cos Ωt или sin Ωt для амплитудной.

1. Обе функции, как А(t), так и θ(t), четные относительно t:

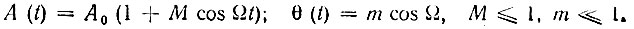
Выражение (3.52) принимает вид

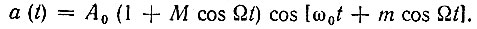
Полагая, как в § 3.3, справедливыми приближенные равенства cos (m cos Ωt) ≈ 1, sin (m cos Ωt) ≈ m cos Ωt, приводим это выражение к виду, аналогичному (3.32):

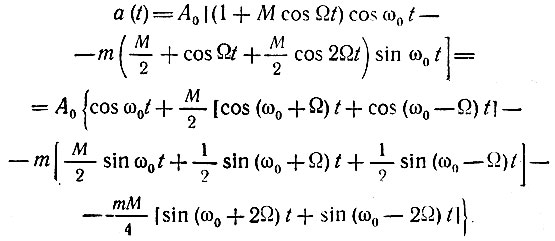
Суммируя квадратурные составляющие 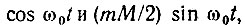получаем для амплитуды результирующего колебания на частоте ω₀ следующее выражение: 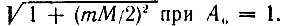Аналогичным образом находим амплитуду 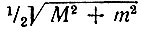для колебаний с частотами 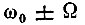и mМ/4 для частот 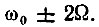Спектр колебания а(t) представлен на рис. 3.22, а. Амплитудный спектр симметричен.

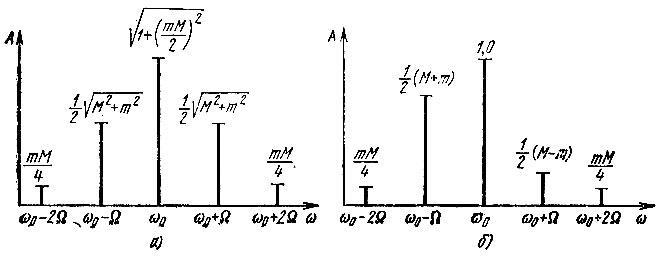
Рис. 3.22. Спектр колебания при одновременной модуляции амплитуды и частоты гармонической функцией

2. Функция θ(t) - четная, а A(t) - сумма четной и нечетной составляющих:

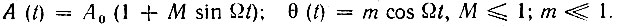
Выкладки, аналогичные предыдущим, приводят к следующим амплитудам: к 1 при частоте ω₀; к ¹/₂(М - m) при частоте ω₀ + Ω; к ¹/₂(М + m) при частоте ω₀ - Ω; к mМ/4 при частотах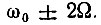

Спектральная диаграмма представлена на рис. 3.22, б.

Симметрия спектра нарушается в данном примере из-за неодинаковых амплитуд колебаний верхней и нижней боковых частот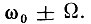

Нарушение симметрии спектра при смешанной амплитудно- частотной модуляции иногда используется как показатель неправильности работы устройства, осуществляющего амплитудную модуляцию; перекос спектра указывает на то, что полезная амплитудная модуляция сопровождается паразитной угловой модуляцией.