3.9. Огибающая, фаза и частота узкополосного сигнала

Современное состояние радиотехники характеризуется непрерывным усовершенствованием способов передачи информации. Это развитие идет по линии изыскания новых видов сигналов и новых способов их обработки.

Рассмотренные в предыдущих параграфах модулированные колебания являются лишь простейшими видами радиосигналов. Часто приходится иметь дело с радиосигналами, получаемыми в результате одновременной модуляции амплитуды и частоты (или фазы) колебания по весьма сложному закону.

В любом случае предполагается, что заданный сигнал a(t) представляет собой узкополосный процесс. Это означает, что все спектральные составляющие сигнала группируются в относительно узкой по сравнению с некоторой центральной частотой ω₀ полосе.

При представлении подобных сигналов в форме

возникает неоднозначность в выборе функций A(t) и ψ(t), так как при любой функции ψ(t) всегда можно удовлетворить уравнению (3.52) надлежащим выбором функции А(t).

Так, например, при желании простейшее (гармоническое) колебание

можно представить в форме

где ω = ω₀ + Δω.

В выражении (3.58') огибающая А(t) в отличие от А₀ является функцией времени, которую можно определить из условия

откуда

Из этого примера видно, что при нерациональном выборе аргумента ψ(t) (ωt вместо ω₀t) очень усложнилось выражение для А(t), причем эта новая функция А(t) по существу не является "огибающей" в общепринятом смысле, так как она может пересекать кривую а(t) (вместо касания в точках, где a(t) имеет максимальное значение). Оперирование подобной "огибающей" не имеет смысла, а в некоторых случаях и недопустимо, так как может привести к ошибочным практическим выводам (например, при рассмотрении работы амплитудного детектора).

Неопределенности можно избежать при представлении A(t) и ψ(t) с помощью следующих соотношений:

где а₁(t) - новая функция, связанная с исходной функцией соотношениями

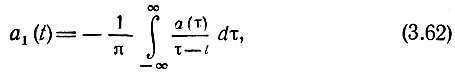
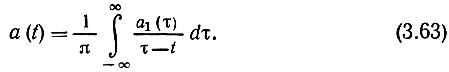
Эти соотношения называются преобразованиями Гильберта, а функция а₁(t) - функцией, сопряженной (по Гильберту) функции а(t).

В соответствии с выражениями (3.60), (3.61) рассматриваемая функция а(t) представлена в виде проекции вектора А(t) на ось абсцисс, относительно которой отсчитывается угол ψ(t) (рис. 3.23).

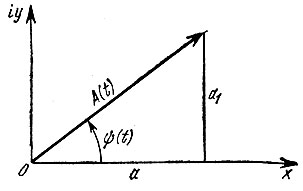
Рис. 3.23. К определению огибающей амплитуд высокочастотного колебания по Гильберту

Для выяснения смысла выражений (3.60), (3.61), а также требования, чтобы а₁(t) являлась функцией, сопряженной по Гильберту исходной функции а(t), рассмотрим сначала некоторые свойства А(t), вытекающие непосредственно из выражения (3.60) и справедливые при любой функции а₁(t).

Прежде всего мы видим, что в точках, где функция а₁(t) равна нулю, имеет место равенство A(t) = а(t).

Дифференцируя (3.60), получаем

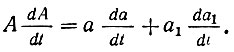
Отсюда видно, что при а₁ = 0, когда А(t) = a(t), имеет место дополнительное равенство

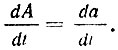
Следовательно, в точках, в которых a₁(t) = 0, кривые А(t) и a(t) имеют общие касательные.

Этих условий, однако, еще недостаточно для того, чтобы можно было рассматривать А(t) как "простейшую" огибающую быстро осциллирующей функции а(t). Необходимо потребовать, чтобы кривая A(t) касалась кривой а(t) в точках, в которых последняя имеет амплитудное или достаточно близкое к нему значение. Иными словами, в точках, где а₁(t) обращается в нуль, функция а(t) должна принимать значения, близкие к амплитудным. Это условие как раз и обеспечивается, если функция а₁(t) является сопряженной по Гильберту функции a(t). Это свойство преобразований Гильберта нагляднее всего иллюстрируется на примере гармонического сигнала.

Пусть а(t) = cos ω₀t. Найдем сопряженную функцию а₁(t). Применяя общее выражение (3.62) и переходя к новой переменной х = τ - t, находим

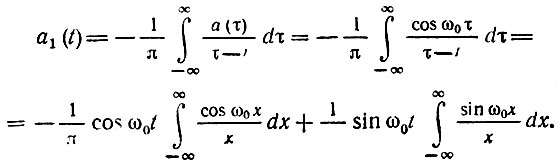
Известно, что

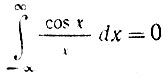
(в смысле главного значения) и

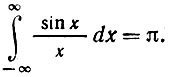
Следовательно, функции a(t) = cos ω₀t соответствует сопряженная функция

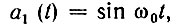
которая проходит через нуль в моменты, когда исходная функция проходит через максимум. Аналогичным образом нетрудно убедиться, что функции a(t) = sin ω₀t соответствует сопряженная функция

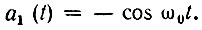
Подставляя 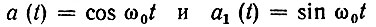в выражение (3.60), получаем для огибающей гармонического колебания общепринятое выражение

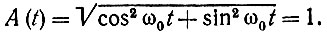
Аналогичный результат получается и для a(t) = sin ω₀t, а₁(t) = - cos ω₀t.

Как видим, выражение (3.60) определяет огибающую в виде линии, касательной к точкам максимума исходной функции, и в случае гармонического колебания соединяющей два соседних максимума кратчайшим путем - прямой линией. Таким образом, выражение (3.60) определяет "простейшую" огибающую. Это свойство выражения (3.60) сохраняется и для сложного сигнала, если выполняется условие медленности изменения огибающей, т. е. если речь идет об узкополосном сигнале [см. выражения (3.2), (3.3)].

Если исходный сигнал представляет собой сумму спектральных составляющих

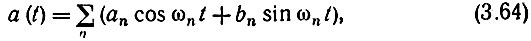
то сопряженная функция

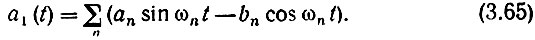
Ряд (3.65) называется рядом, сопряженным ряду (3.64).

Если сигнал а(t) представлен не рядом (3.64), а интегралом Фурье

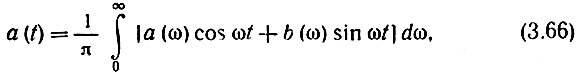
то функция а₁(t) может быть представлена в виде интеграла

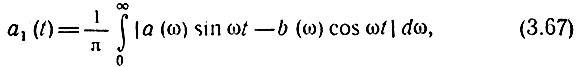
сопряженного интегралу (3.66).

Нетрудно установить связь между спектрами функций а(t) и а₁(t). Так как при преобразовании гармонического колебания по Гильберту его амплитуда остается неизменной, то очевидно, что по модулю спектральная плотность S₁(ω) сопряженной функции а₁(t) не может отличаться от спектральной плотности S(ω) исходной функции а(t). Фазовая же характеристика спектра S₁(ω) отличается от фазовой характеристики спектра S(ω). Из сопоставления выражений (3.67) и (3.66) непосредственно вытекает, что все спектральные составляющие функции а₁(t) отстают по фазе на 90° от соответствующих составляющих функции а (0. Следовательно, при ω > 0 спектральные плотности S₁(ω) и S(ω) связаны соотношением

В области отрицательных частот соответственно получается

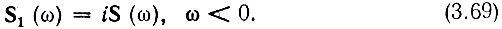
Вследствие изменения фазовой характеристики сопряженная функция а₁(t) по своей форме может сильно отличаться от исходной функции a(t).

Нетрудно, наконец, заметить, что если исходный сигнал записан в форме

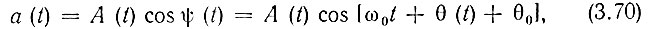
где огибающая А(t) определена соотношением (3.60), то сопряженную функцию можно записать в аналогичной форме

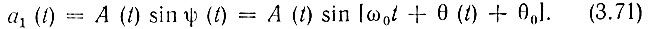
Это вытекает непосредственно из определения (3.61) и рис. 3.23.

После того как найдена сопряженная функция а₁(t), нетрудно с помощью выражений (3.60), (3.61) найти огибающую А(t), полную фазу ψ(t) и, наконец, мгновенную частоту узкополосного сигнала

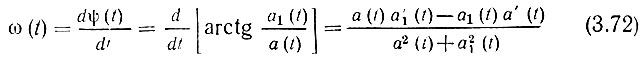
Выделив в найденной таким образом частоте ω(t) постоянную часть ω₀, можно написать выражение для ψ(t):

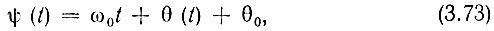
в котором θ(t) не содержит слагаемого, линейно зависящего от времени. Тем самым устраняется произвол в выборе "средней частоты" сигнала ω₀ и соответственно функции θ(t).

Поясним применение преобразования Гильберта для определения огибающей фазы и мгновенной частоты сигнала на следующем примере.

Пусть задан сигнал в виде суммы двух гармонических колебаний с близкими частотами ω₁ и ω₂;

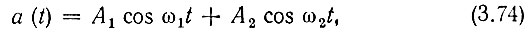
и требуется а(t) представить в форме

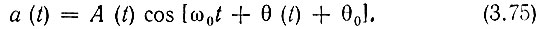
Расстройка 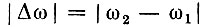полагается настолько малой по сравнению с (ω₁ + ω₂)/2, что колебанием a(t) можно считать узкополосным.

Что следует в данном случае подразумевать под А(t), ω₀ и θ(t)? Непосредственно из выражения (3.74) трудно выявить структуру огибающей и фазы результирующего колебания а(t). Используем поэтому выражения (3.60), (3.61). Сопряженная функция

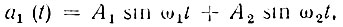
Применяя формулу (3.60), находим огибающую сигнала а(t):

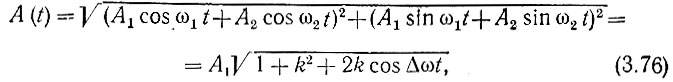
где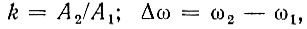

причем для определенности считается, что k < 1 и Δω > 0. Полную фазу суммарного колебания находим по формуле (3.61):

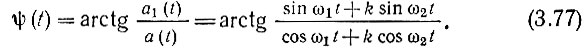
Применяя далее формулу (3.72), после несложных алгебраических и тригонометрических преобразований приходим к следующему выражению для мгновенной частоты:

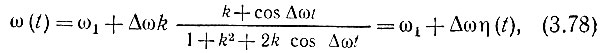
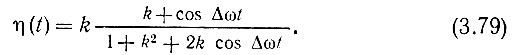
Так как постоянная составляющая функции η(t) равна нулю, то входящие в выражение (3.73) средняя частота ω₀ и функция θ(t) будут

Итак, на основании (3.76), (3.78) и (3.80)-(3.81) выражение (3.75) приводится к виду

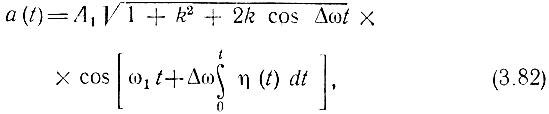
где η(t) определяется выражением (3.79).

При этом исключается произвол и неопределенность в выборе огибающей и фазы суммарного колебания.

Графики функции η характеризующие изменение частоты приведены на рис. 3.24 для некоторых значений k. При k → 1 получаются выбросы, описываемые дельта-функциями. Это соответствует производным скачкообразно изменяющейся фазы (на 180°) в моменты времени, когда огибающая биений обращается в нуль. При k << 1, т. е. при наложении слабого колебания А₂ cos ω₂t на сильное А₁ cos ω₁t, выражения (3.76)-(3.79) значительно упрощаются:

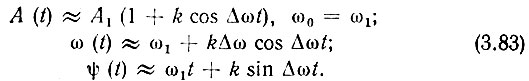
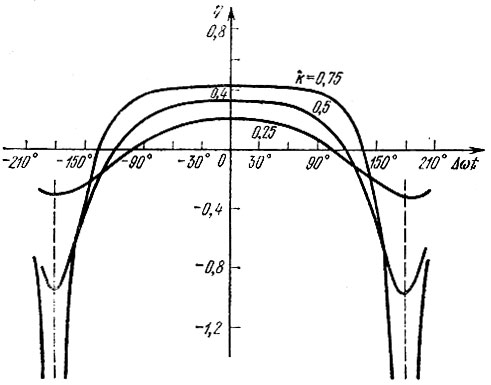
Рис. 3.24. Мгновенная частота колебания, являющегося суммой двух гармонических колебаний

В этом случае огибающая, частота и фаза суммарного колебания изменяются по гармоническому закону с частотой |Δω| = |ω₂ - ω₁ относительно своих средних значений соответственно А₁, ω₁ и ω₁t.

Формулы (3.76)-(3.83) имеют большое прикладное значение, так как в радиотехнической практике часто приходится иметь дело с биениями двух гармонических колебаний.

В заключение следует отметить, что в некоторых специальных случаях выражения (3.60)-(3.69) используют также и для широкополосных сигналов, когда понятие "огибающая" амплитуд теряет свой обычный смысл. При этом отказываются от требования, чтобы огибающая А(t) касалась кривой а(t) вблизи точек, в которых а(t) имеет амплитудное значение.