3.10. Аналитический сигнал

В электротехнике принято представлять гармоническое колебание (ток, напряжение) в форме

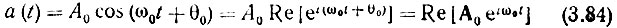
или

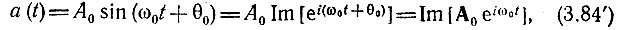
где 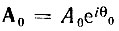- комплексная амплитуда.

Часто символы Re или Im опускают и пишут просто

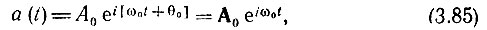
подразумевая действительную или мнимую часть этого выражения.

В современной радиотехнике представление колебаний в комплексной форме получило дальнейшее развитие и распространено на негармонические колебания.

Если задан физический сигнал в виде действительной функции а(t), то соответствующий ему комплексный сигнал представляется в форме

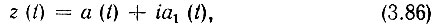
где а₁(t) - функция, сопряженная по Гильберту сигналу а(t).

Определенная таким образом комплексная функция z(t) называется комплексным или аналитическим сигналом, соответствующим физическому сигналу а(t). Заметим, что и в выражении (3.85) мнимая часть комплексной функции является функцией, сопряженной по Гильберту действительной части.

При представлении а(t) и а₁(t) в форме выражений (3.70), (3.71) аналитический сигнал можно записать следующим образом:

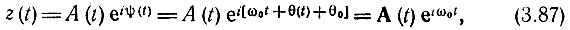
где

представляет собой комплексную огибающую узкополосного сигнала. Модуль комплексной огибающей, равный A(t) [поскольку |e^{i[θ(t) + θ₀]}| = 1 при любом законе изменения θ(t)], содержит информацию только об амплитудной модуляции колебания, а фазовый множитель е^iθ(t) - только об угловой модуляции. В целом же произведение А(t)е^iθ(t) содержит полную информацию о сигнале а(t) (за исключением несущей частоты ω₀, которая предполагается известной).

Это свойство комплексной огибающей, позволяющее при анализе узкополосных сигналов исключать из рассмотрения частоту ω₀, придает важное значение понятию "аналитический сигнал".

Рассмотрим основные свойства аналитического сигнала и комплексной огибающей.

1. Произведение аналитического сигнала z_a(t) на сопряженный ему сигнал z*_a(t) равно квадрату огибающей исходного (физического) сигнала a(t).

Действительно,

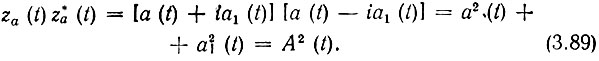
Таким образом, модуль аналитического сигнала z_a(t) равен просто огибающей сигнала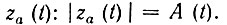

2. Спектр аналитического сигнала содержит только положительные частоты.

Из выражения

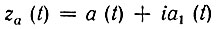
вытекает, что спектральная плотность Z(ω) аналитического сигнала z_a(t) определяется суммой

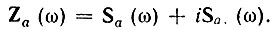
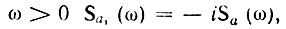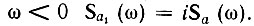Но согласно (3.68), (3.69) при а при Следовательно,

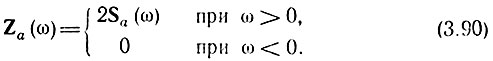
Так, например, если узкополосному сигналу а(t) соответствует спектральная плотность S_a(ω), модуль которой изображен на рис. 3.25 штриховой линией, то аналитическому сигналу z_a(t) = а(t) + ia₁(t) соответствуют спектральная плотность Z_a(ω), модуль которой изображен на том же рисунке сплошной линией.

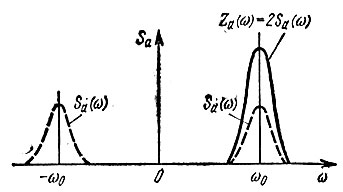
Рис. 3.25. Соотношение между спектрами физического и аналитического сигналов

Интеграл Фурье для аналитического сигнала z_a(t) принимает^* следующий вид:

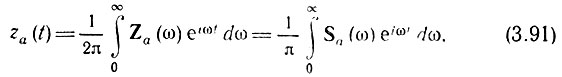
^* (Отсюда проясняется смысл термина "аналитический сигнал". Действительно, при переходе к комплексному t интеграл (3.91) сходится в верхней полуплоскости и является аналитической функцией при Im t > 0, поскольку при ω → ∞ множитель e^iωImt обеспечивает сходимость. В случае же физического сигнала, содержащего как положительные, так и отрицательные частоты, множитель e^iωImt бесконечно возрастает либо при ω → +∞, либо при ω → -∞.)

где S_a(ω) - спектральная плотность исходного (физического) сигнала a(t).

3. Спектральная плотность комплексной огибающей А(t) совпадает со смещенной на величину ω₀ влево спектральной плотностью аналитического сигнала z_a(t).

Основываясь на общей формуле (2.48), можем написать

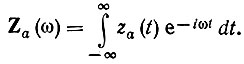
Подставляя в это выражение z_a(t) = A(t)е^iω₀t, получаем

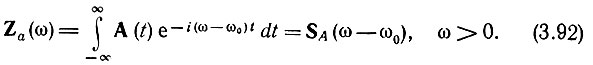
Это соотношение является обобщением формулы (2.58) на случай комплексной функции времени А(t), умножаемой на е^iω₀t (вместо cos ω₀t в § 2.7, п. 3). Выражение (3.9), выведенное для вещественной огибающей А(t) (при чисто амплитудной модуляции), является частным случаем общего выражения (3.92).

Вводя обозначение ω - ω₀ = Ω, перепишем (3.92) в несколько иной форме

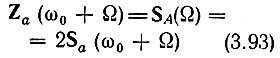
[см. формулу (3.90)].

Соотношение между спектрами S_A(Ω) и Z_а(ω₀ + Ω) иллюстрируется рис. 3.26.

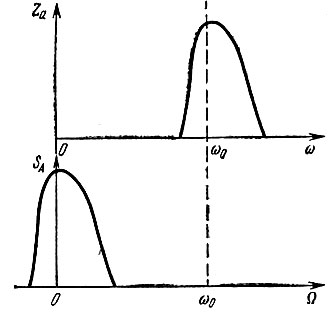
Рис. 3.26. Соотношение между спектрами аналитического сигнала и комплексной огибающей исходного сигнала

Особо следует отметить, что спектр S_A(Ω) комплексной огибающей А(t) не обязательно симметричен относительно нулевой частоты (см. рис. 3.26). Если спектр S_a(ω) физического колебания а(t) несимметричен относительно ω = ω₀, как это может иметь место, например, при смешанной амплитудно-угловой модуляции (см. § 3.8), то и функция Z_a(ω) = 2S_a(ω), ω > 0, несимметрична; после сдвига Z_a(ω) на величину ω₀ влево спектр комплексной огибающей Z_a(ω) будет несимметричен относительно частоты Ω = 0. Поскольку при таком сдвиге функция S_A(Ω) отлична от нуля в области частот Ω < 0, комплексная функция А(t) не является аналитическим сигналом. Это объясняется тем, что действительная и мнимая части A(t) не являются функциями, сопряженными по Гильберту.

4. Корреляционная функция аналитического сигнала, определяемая выражением

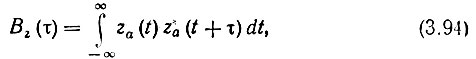
связана с корреляционной функцией исходного физического сигнала (узкополосного)

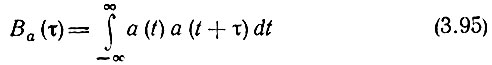
соотношением

Действительно, подставив в (3.94) 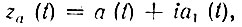получим

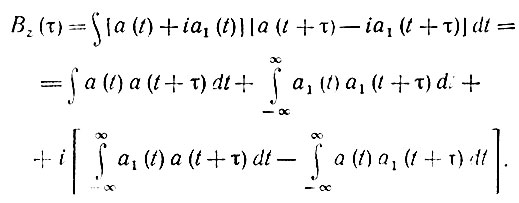
В § 2.17 было установлено, что корреляционная функция физического сигнала зависит только от модуля его спектральной плотности. Так как модули спектров функций a(t) и а₁(t) одинаковы (см. § 3.9), то первые два интеграла равны и суммируются, а вторые два взаимно уничтожаются из чего и следует соотношение (3.96). Подставив теперь в (3.94) 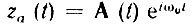и 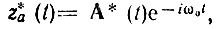получим

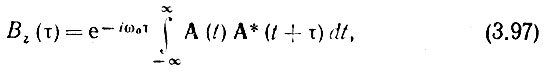
откуда вытекает важное соотношение [см. (3.96)]

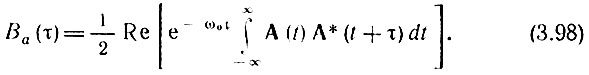
Входящий в выражение (3.98) интеграл есть корреляционная функция комплексной огибающей А(t). Поэтому выражение (3.98) можно переписать в форме

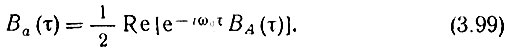
В частности, при τ = 0 получаем

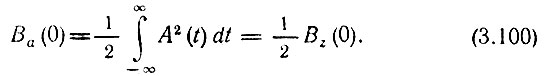
Из этого выражения видно, что поскольку В_а(0) = Э, энергия аналитического сигнала равна удвоенной энергии исходного физического сигнала.

Следует указать, что применение понятия энергии к комплексной функции имеет не только формальный смысл. В гл. 12 будет показано, что в некоторых устройствах обработки сигналов приходится иметь дело с совокупностью двух функций времени, сопряженных по Гильберту, т. е. с аналитическим сигналом как с физическим процессом.

Преимущества аналитического сигнала при анализе узкополосных процессов будут видны из дальнейших глав.