3.11. Корреляционная функция модулированного колебания

При нахождении корреляционной функции модулированного колебания a(t) = A(t) cos ψ(t) будем исходить из условия абсолютной интегрируемости (конечной энергии) колебания а(t), что позволяет применять определение (см. § 2.16)

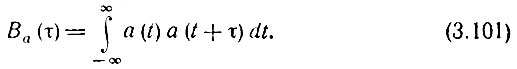
Вычисление интеграла для сложных сигналов требует громоздких выкладок. Задача существенно упрощается при переходе от колебания a(t) к аналитическому сигналу z_a(t) = А(t) е^iω₀t. Основываясь на соотношениях, выведенных в предыдущем параграфе, рассмотрим сначала чисто амплитудную модуляцию, когда a(t) = A(t) cos ω₀t, θ(t) = 0 и, следовательно, A(t) = A*(t) = A(t).

Тогда формула (3.98) принимает вид

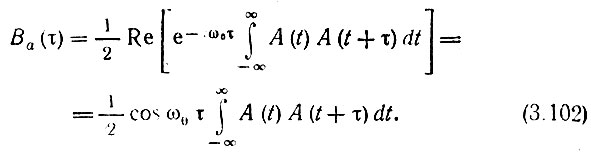
Обозначив, как и в выражении (3.99), интегральный множитель через В_А(τ), окончательно получим

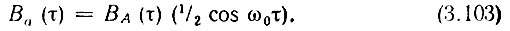
Второй множитель 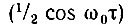есть корреляционная функция гармонического колебания с частотой ω₀ и единичной амплитудой.

Итак, корреляционная функция амплитудно-модулированного радиосигнала равна произведению корреляционных функций огибающей и высокочастотного заполнения.

В качестве примера на рис. 3.27, а показан радиоимпульс с прямоугольной огибающей, а на рис. 3.27, б - соответствующая этому импульсу корреляционная функция. Следует отметить, что эта функция не зависит от начальной фазы заполнения радиоимпульса, а ее огибающая совпадает с корреляционной функцией прямоугольного видеоимпульса (см. § 2.16, рис. 2.38, г).

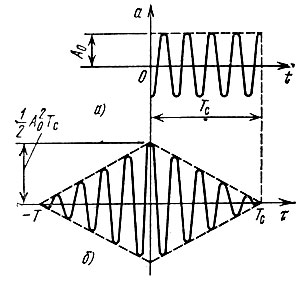
Рис. 3.27. Импульс с высокочастотным заполнением (a) и корреляционная функция (б)

Для иллюстрации применения общего выражения (3.99) к амплитудно-частотной модуляции найдем корреляционную функцию импульса, изображенного на рис, 3.19, а.

При обозначениях формулы (3.37) и рис. 3.19 аналитический сигнал запишется в виде

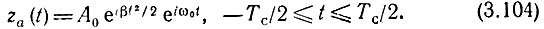
Применяя формулы (3.94) и (3.99), получаем

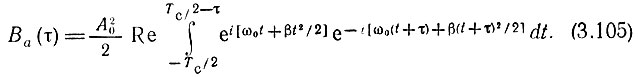
Пределы интегрирования взяты с учетом условия одновременного существования функций a(t) и a(t + τ) (рис. 3.28).

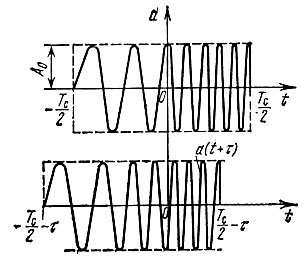
Рис. 3.28. К построению корреляционной функции ЛЧМ импульса

С помощью несложных преобразований выражение (3.105) приводится к виду

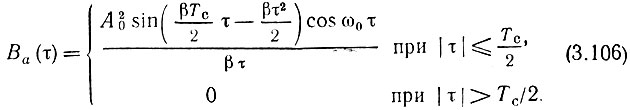
Используя введенный в § 3.7 параметр m [см. формулу (3.38)] и учитывая, что 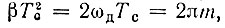приведем выражение (3.106) к несколько более общему виду

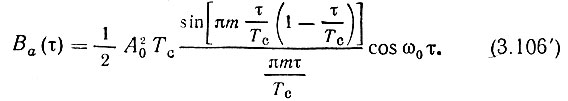
Множитель 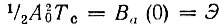равен полной энергии рассматриваемого радиоимпульса (как и при импульсе с постоянной частотой заполнения, см. рис. 3.27, б).

Таким образом,

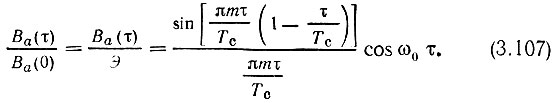
График этой функции построен на рис. 3.29 для параметра m = 100 в предположении, что ω₀Т₀ очень велико (на рис. 3.29 масштаб выбран произвольно). Огибающая корреляционной функции образует весьма острый пик (при m >> 1), а частота заполнения постоянна и равна центральной частоте ω₀ исходного радиоимпульса.

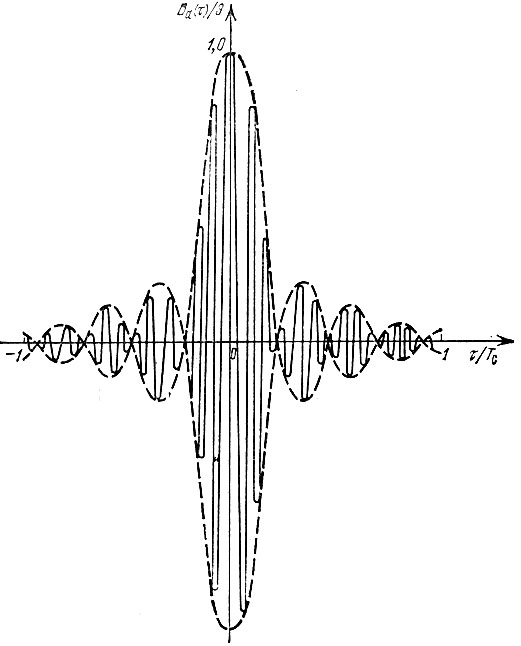
Рис. 3.29. Корреляционная функция ЛЧМ импульса

Рассмотренный здесь сигнал и его корреляционная функция представляют большой практический интерес для современной радиотехники.