3.12. Дискретизация узкополосного сигнала

Пусть задан сигнал

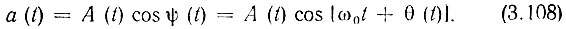
спектр которого заключен в узкой полосе частот от ω₁ до ω₂, так что модуль спектральной плотности S_a(ω) имеет вид, представленный на рис. 3.30, а, причем в пределах полосы Δω₀ спектр не обязательно симметричен относительно центральной частоты ω₀ = (ω₁ + (ω₂)/2. Под узкополосностью сигнала подразумевается условие

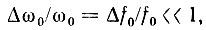
где 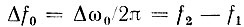- полоса частот, Гц.

Предполагается, что функция A(t) является простейшей огибающей, т. е. что A(t) и ψ(t) отвечают соотношениям (3.60) и (3.61).

Если при дискретизации подобного сигнала исходить из ряда (2.120), то интервал между выборками должен быть не больше чем 1/2f₂, где f₂ - наивысшая частота в спектре сигнала. Нецелесообразность такого подхода очевидна, так как информация о сигнале заложена не в частоту f₂ (или f₁), а в огибающую A(t) или в фазу θ(t), которые изменяются во времени медленно, с относительно низкими частотами модуляции. Желательно поэтому так преобразовать выражение (2.120), чтобы интервалы между выборками определялись фактической шириной спектра, т. е. величиной Δf₀, а не верхней частотой f₂.

Для этого перейдем к аналитическому сигналу, соответствующему заданной функции a(t):

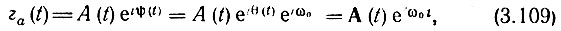
где комплексная огибающая A(t) = А(t) е^iθ(t) представляет собой низкочастотную функцию, спектр которой S_A(Ω) примыкает к нулевой частоте (рис. 3.30, б). Разложим комплексную функцию A(t) = А (t) е^iθ(t) по ортогональной системе

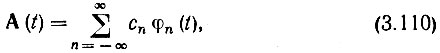
где базисная функция φ_n(t) определяется выражением (2.121).

Подставив этот ряд в (3.109), получим

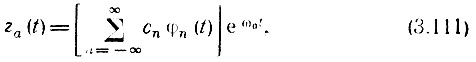
после чего исходное колебание a(t) определим как действительную часть функции z_a(t):

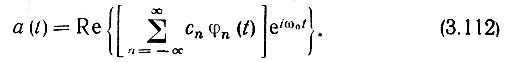
Как видим, задача дискретизации высокочастотного колебания свелась к задаче дискретизации комплексной огибающей А(t). При определении наибольшего допустимого интервала между выборками в разложении (3.110) необходимо исходить из наивысшей частоты в спектре функции А(t), Из определения ω₀ как средней частоты в полосе Δω₀ очевидно, что эта частота, отсчитываемая от Ω = 0, равна Δω₀/2, или в герцах Δf₀/2. Следовательно, интервал между выборками не должен превышать

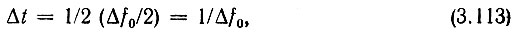
а функция φ_n(t) должна иметь вид

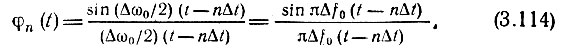
От аналогичной функции, использованной в § 2.14, φ_n(t) отличается только заменой ω_m на Δω₀/2. Следовательно, спектральная плотность Ф₀(Ω) функции 966;₀(t) равна 2π/Δω₀ = 1/Δf₀ в полосе частот 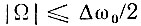(рис. 3.30), а спектральная плотность функции φ_n(t)

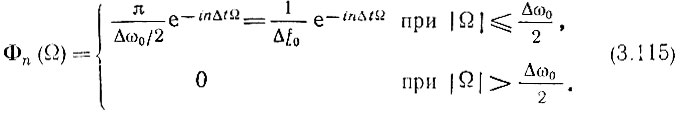
Квадрат нормы функции φ_n(t) по аналогии с выражением (2.123)

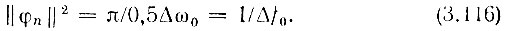
Далее по формуле (2.9) с учетом (3.116)

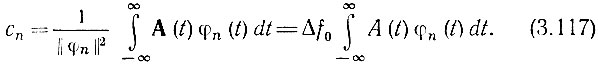
Используя формулу (2.63), в которой заменяем ω на Ω^*, получаем

^* (Поскольку здесь рассматривается спектр огибающей.)

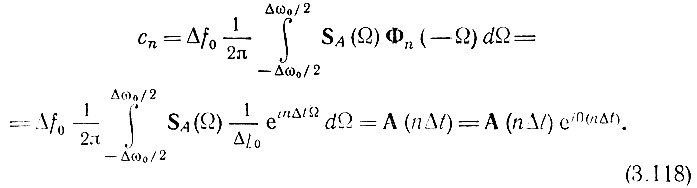
В выражении (3.118) S_A - спектр комплексной огибающей А(t), а A(nΔt) - ее значение в отсчетной точке t = nΔt.

Итак, коэффициенты ряда (3.110) являются выборками функции А(t), взятыми через интервалы Δt = 1/Δf₀.

Подставляя (3.118) в (3.111), получаем

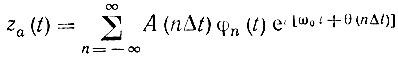
и по формуле (3.112) определяем

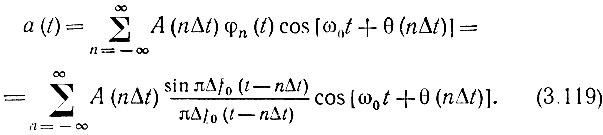
При заданной длительности сигнала Т_с число отсчетных точек 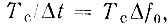причем в каждой точке должны быть заданы два параметра: A(nΔt) и θ(nΔt).

Следует иметь в виду, что при несимметричном (в полосе Δω₀) спектре введенная в данном параграфе частота ω₀ = (ω₁ + ω₂)/2 может не совпадать со "средней частотой" в выражении (3.73). Иными словами, фаза θ(t) может содержать слагаемое, линейно зависящее от времени.

Проиллюстрируем выражение (3.119) на примерах колебания, промодулированного по амплитуде или по частоте.

При AM исходим из колебания a(t) = А(t) cos ω₀ в котором А(t) - вещественная функция со спектром S_A(ω), ограниченным наивысшей частотой Ω_m = 2πF_m. В этом случае ширина спектра модулированного колебания a(t) равна Δf_ам = 2F_m, причем в пределах этой полосы спектральная плотность S_a(ω) симметрична относительно ω₀. Интервал между выборками в соответствии с формулой (3.113) должен быть не больше чем Δt = 1/Δf_ам = 1/2F_m, т. е. таким же как и при дискретизации исходного сообщения (модулирующего напряжения).

Так как фаза высокочастотного заполнения при чисто амплитудной модуляции постоянна, то передавать ее нет необходимости. Отсюда вытекает очевидный результат: амплитудно-модулированное колебание вполне определяется значениями своих амплитуд, взятыми через интервал 1/2F_m, где F_m - верхняя частота в спектре модулирующей функции (т. е. в спектре передаваемого сообщения).

Иными словами, при чисто амплитудной модуляции число степеней свободы модулированного колебания такое же, как и число степеней свободы модулирующей функции.

Рассмотрим теперь частотно-модулированное колебание

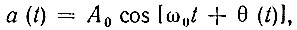
когда мгновенная частота ω(t) = ω₀ + dθ/dt модулирована тем же сообщением, что и в предыдущем случае, причем максимальная девиация частоты f_д велика по сравнению с F_m, так что ширину Δf_чм полосы частот модулированного колебания можно приравнять к 2f_д [случай "широкополосной" частотной модуляции, (3.34)]. Интервал между выборками должен быть взят Δt ≤ 1/Δf_чм = 1/2f_д. Так как при ЧМ амплитуда колебания неизменна, то передавать ее нет необходимости. Следовательно, для однозначного представления частотно-модулированного колебания достаточно задавать фазу θ (nΔt) этого колебания в отсчетных точках, отстоящих одна от другой на время Δt ≤ 1/2f_д. При одной и той же длительности сообщения Т_с число выборок фазы при ЧМ равно Δf_чмT_с = 2f_дТ_с, а число выборок огибающей при АМ равно Δf_амT_c = 2F_mT_c. Отсюда видно, что при одинаковом передаваемом сообщении (при одинаковом количестве информации) частотно-модулированный сигнал обладает числом степеней свободы в f_д/F_m = m раз большим, чем амплитудно-модулированный сигнал. Это является результатом расширения спектра сигнала при ЧМ. На приемной стороне канала связи после частотного детектирования модулированного колебания выделяется напряжение, которое имеет спектр и число степеней свободы такие же, как и исходное сообщение.

Из приведенного примера видно, что при одной и той же ширине спектра информационная емкость радиосигнала различна в зависимости от вида модуляции.

При смешанной модуляции - амплитудной и угловой - в каждой отсчетной точке нужно брать две выборки: амплитуды и фазы.