4.2. Виды случайных процессов. Примеры

Применение общих определений, приведенных в предыдущем параграфе, иллюстрируется ниже на нескольких характерных случайных процессах.

Наряду с обозначением случайного процесса символом X(t) будет применяться в том же смысле обозначение х(t), под которым подразумевается случайная функция времени. Как и ранее, x_k(t) обозначает k-ю реализацию случайной функции х(t).

1. Сигнал в виде постоянного напряжения случайного уровня

Пусть уровень А сигнала может с равной вероятностью принимать любое значение в интервале от - 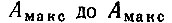(рис. 4.2.)

Рис. 4.2. Совокупность постоянных напряжений случайного уровня

Стационарность этого процесса очевидна. Одномерную плотность вероятности легко получить из выражения (4.2):

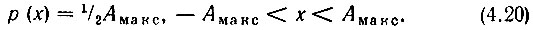
Подстановка (4.20) в выражения (4.3)-(4.5) дает

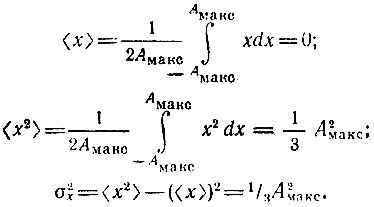
При определении корреляционной функции по формуле (4.6) следует учитывать, что для любой реализации, независимо от временного сдвига τ, выполняется равенство 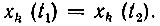Следовательно, 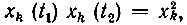и усреднение этого произведения по множеству можно выполнить без использования двумерной плотности вероятности, непосредственно по формуле (4.8). Таким образом,

Рассматриваемый процесс не эргодичен. Это видно из того, что

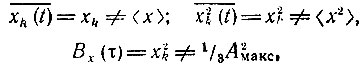
т. е. первые два момента и корреляционная функция, определенные усреднением по времени (вдоль реализаций), не совпадают с результатом усреднения по множеству.

2. Гармоническое колебание со случайной амплитудой

Пусть в выражении, определяющем сигнал

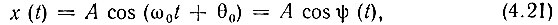
частота ω₀ и начальная фаза θ₀ являются детерминированными и постоянными величинами, а амплитуда А - случайная, равновероятная в интервале от 0 до А_макс величина (рис. 4.3).

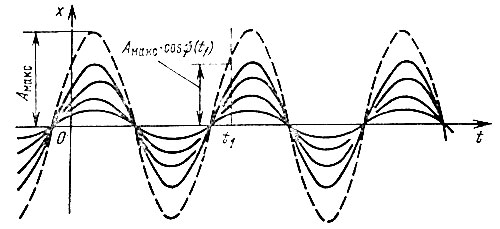
Рис. 4.3. Совокупность гармонических колебаний со случайной амплитудой

Найдем одномерную плотность вероятности р(х; t₁) для фиксированного момента времени t₁. Мгновенное значение х(t₁) может принимать любые значения в интервале от 0 до A_макс cos ψ (t₁), причем будем считать, что cos ψ (t₁) > 0. Следовательно,

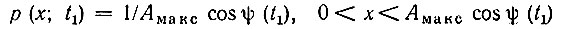
и математическое ожидание

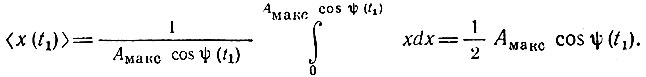
Далее,

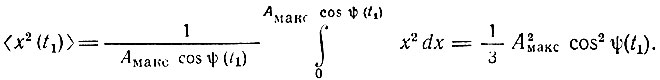
Наконец, дисперсия

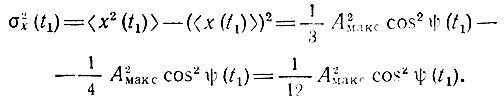
Рассматриваемый случайный процесс нестационарный и не эргодический.

3. Гармоническое колебание со случайной фазой

Пусть амплитуда А₀ и частота ω₀ гармонического сигнала заранее достоверно известны, а начальная фаза θ - случайная величина, которая с одинаковой вероятностью может, принимать любое значение в интервале от -π до π. Это означает, что плотность вероятности начальной фазы

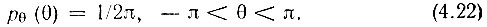
Одну из реализаций случайного процесса х(t), образуемого совокупностью гармонических колебаний со случайными фазами (рис. 4.4), можно определить выражением

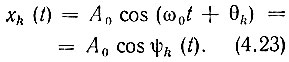
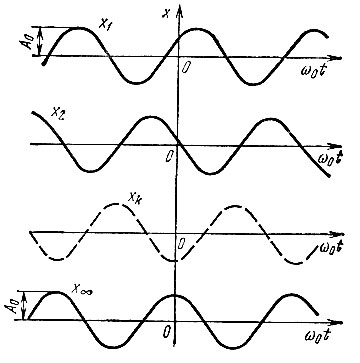
Рис. 4.4. Совокупность гармонических колебаний со случайными фазами

Полная фаза колебания ψ(t) = ω₀t + θ является случайной величиной, равновероятной в интервале от ω₀t - π до ω₀t + π, следовательно,

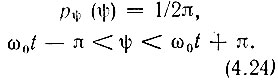
Найдем одномерную плотность вероятности р_х(х) случайного процесса X(t). Выделим интервал х, х + dx (рис. 4.5) и определим вероятность того, что при измерении величины сигнала, проведенном в промежутке времени от t₁ до t₁ + dt, мгновенное значение сигнала окажется в интервале х, х + dx. Эту вероятность можно записать в виде р_х(х) dx, где р_х(х) - искомая плотность вероятности. Очевидно, что вероятность р_х(х) dx совпадает с вероятностью попадания случайной фазы колебаний ψ в один из двух заштрихованных на рис. 4.5 фазовых интервалов. Эта последняя вероятность равна 2р_ψ(ψ) dψ. Следовательно,

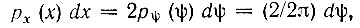
откуда искомая функция^*

^* (Абсолютное значение производной берется на том основании, что плотность вероятности является неотрицательной функцией.)

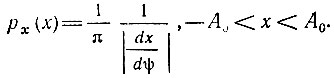
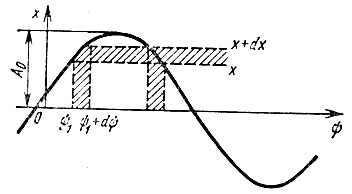
Рис. 4.5. К определению плотности вероятности гармонического колебания со случайной фазой

Но,

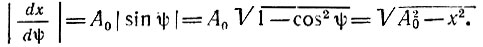
Таким образом, окончательно

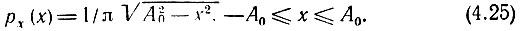
График этой функции изображен на рис. 4.6.

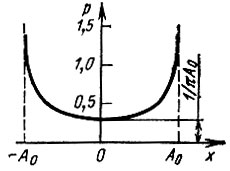
Рис. 4.6. Плотность вероятности гармонического колебания со случайной фазой

Существенно, что одномерная плотность вероятности р_х(x) не зависит от выбора момента времени t, а среднее по множеству (см. (2.271.7) в [10])

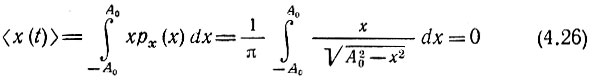
совпадает со средним по времени

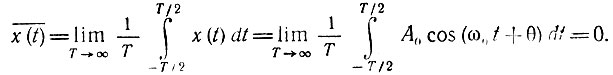
(Это справедливо для любой реализации рассматриваемого случайного процесса.)

Корреляционную функцию в данном случае можно получить усреднением произведения х(t₁) х(t₂) по множеству без обращения к двумерной плотности вероятности [см. общее выражение (4.7)]. Действительно, подставляя в (4.6)

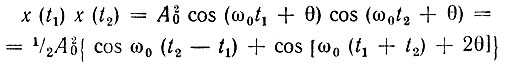
и учитывая, что первое слагаемое cos ω₀ (t₂ - t₁) является детерминированной величиной, а второе слагаемое при статистическом усреднении с помощью одномерной плотности вероятности р_θ(θ) = 1/2π [см (4.22)] обращается в нуль, получаем

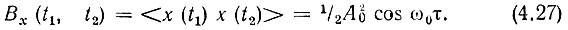
Такой же результат получается и при усреднении произведения x_k(t) x_k(t + τ) по времени для любой реализации процесса.

Независимость среднего значения от t₁ и корреляционной функции от положения интервала τ = t₂ - t₁ на оси времени позволяет считать рассматриваемый процесс стационарным. Совпадение же результатов усреднения по множеству и времени (для любой реализации) указывает на эргодичность процесса. Аналогичным образом нетрудно показать, что гармоническое колебание со случайной амплитудой и случайной фазой образует стационарный, но не эргодический процесс (различные реализации обладают неодинаковой дисперсией).

4. Нормальный случайный процесс

Нормальный (гауссов) закон распределения случайных величин чаще других встречается в природе. Нормальный процесс особенно характерен для помех канала связи. Он очень удобен для анализа. Поэтому случайные процессы, распределение которых не слишком сильно отличается от нормального, часто заменяют нормальным процессом.

Одномерная плотность вероятности нормального процесса определяется выражением

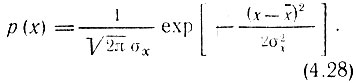
В данном параграфе рассматривается стационарный и эргодический нормальный процесс. Поэтому под 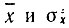можно подразумевать соответственно постоянную составляющую и среднюю мощность флуктуационной составляющей одной (достаточно длительной) реализации случайного процесса.

Графики плотности вероятности при нормальном законе для некоторых значений σ_х изображены на рис. 4.7. Функция р(х) симметрична относительно среднего значения. Чем больше σ_х, тем меньше величина максимума, а кривая становится более пологой [площадь под кривой р(х) равна единице при любых значениях σ_х.

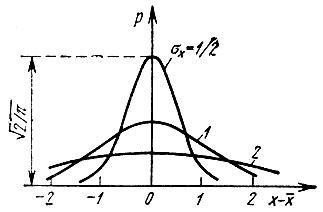
Рис. 4.7. Одномерная плотность вероятности нормального распределения

На основе функции р(х) можно найти относительное время пребывания величины сигнала х(t) в определенном интервале уровней, отношение максимальных значений к среднеквадратическому (пик-фактор) и ряд других важных для практики параметров случайного сигнала. Поясним это на примере одной идеализаций нормального шума, изображенной на рис. 4.8, а для Эта функция времени соответствует шумовой помехе, спектр которой простирается от нулевой частоты до некоторой граничной частоты. Вероятность пребывания значения х(t) в интервале от а до b определяется выражением (4.1). 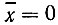Подставляя в это выражение (4.28), при получаем

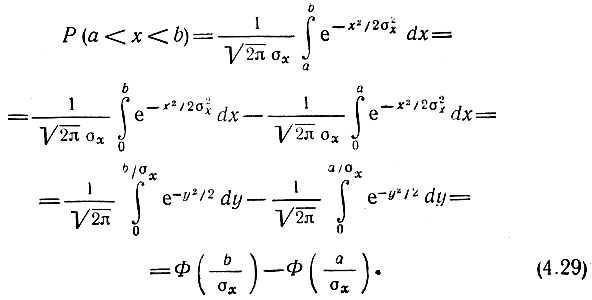
Функция

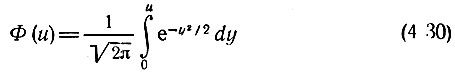
называется интегралом вероятностей. В любом математическом справочнике приводятся таблицы этой функции.

Подставив в (4.29) b/σ_х = 1, 2, 3 и соответственно а/σ_х = -1, -2, и -3, нетрудно найти вероятности пребывания х(t) в полосах шириной 2σ_х, 4σ_х и 6σ_х, симметричных относительно оси t.

В рассматриваемом частном случае (|а| = b) формулу (4.29) можно упростить на основании симметрии функции р(х) относительно оси ординат (рис. 4.7).

Таким образом,

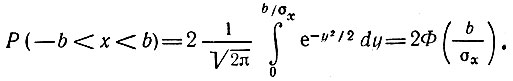
Результаты вычислений сведены в табл. 4.1. В последней графе приведены величины, равные 1 - 2Ф(b/σ_х). Из этой таблицы следует, что ширину шумовой дорожки (рис. 4.8, а) нормального шума можно приравнять (4 - 5) σ_х. Если принимать во внимание пики функции х(t), вероятность которых не менее 1%, то пикфактор шума можно оценить величиной ~3 (отношение пика к σ_х). Напомним, что для гармонического колебания пикфактор равен √2.

Таблица 4.1

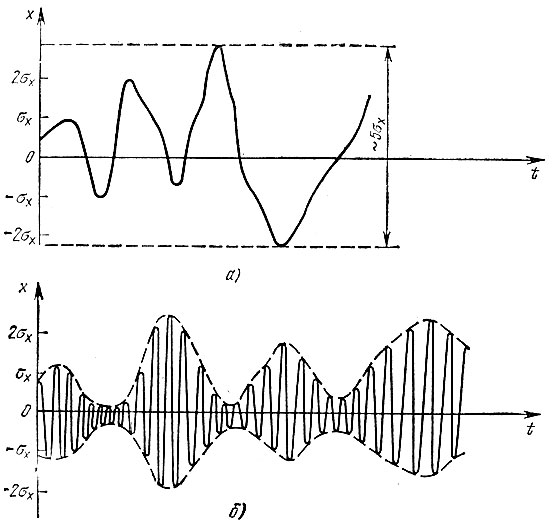
Рис. 4.8. Случайные функции с одинаковым распределением (нормальным), но с различными частотными спектрами

Отношение времени пребывания х(t) в заданном интервале к общему времени наблюдения (достаточно большому для эффективного усреднения) можно трактовать как вероятность попадания х(t) в указанный интервал. На такой трактовке основан принцип построения различных приборов, используемых для экспериментального нахождения одномерной плотности вероятности случайного процесса.

Можно отметить, что приведенные выше данные о распределении вероятностей не дают никаких представлений о поведении функции х(t) во времени. На рис. 4.8, б, показана реализация нормального шума со спектром, сосредоточенным в узкой полосе частот с центральной частотой ω₀. По своей плотности вероятности р(х) и, следовательно, по значениям х¯ и σ_x этот шум не отличается от низкочастотного шума, показанного на рис. 4.8, а.

Для описания временных характеристик функции х(t) необходимо привлечь двумерную плотность вероятности, позволяющую найти корреляционную функцию. Другой способ - нахождение спектра мощности случайного процесса. Он рассматривается в следующем параграфе.