5.6. Апериодический усилитель

Схема замещения простейшего апериодического резистивного усилителя представлена на рис. 5.14, а. Усилительный прибор обозначен в виде зависимого источника тока SΕ₁ с внутренней проводимостью G_i = 1/R_i. Емкость С₀ включает в себя межэлектродную емкость активного элемента, а также емкость внешней цепи, шунтирующей нагрузочный резистор R = 1/G. Схема на рис. 5.14, а является обобщенной, применимой к любому активному элементу.

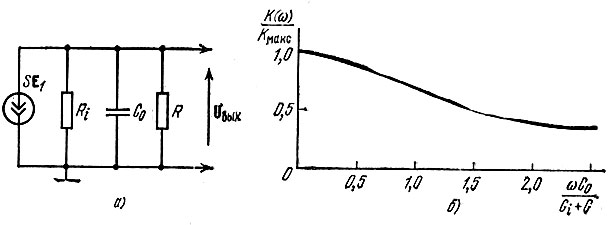
Рис. 5.14. Апериодический транзисторный усилитель ОЭ: а - схема замещения коллекторной цепи, б - частотная характеристика

В случае транзисторного усилителя под крутизной S следует подразумевать величину h_21э/R_вх (см. § 5.4), а под G_i - параметр h₂₂.

Подставив в формулу (5.35') проводимость G_i вместо h₂₂, а также 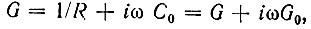получим передаточную функцию усилителя

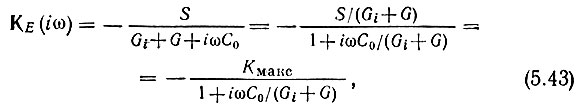
где

- максимальный коэффициент усиления (при ω → 0).

Модуль передаточной функции

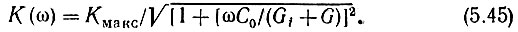
При изменении частоты со получается амплитудно-частотная характеристика, изображенная на рис. 5.14, б.

В апериодических усилителях, работающих на пентодах, часто применяется схема, представленная на рис. 5.15, а. От схемы на рис. 5.13, а, эта схема отличается дополнительной цепью R₁, C₁, назначение которой заключается в защите выходных цепей усилителя от источника постоянного напряжения Е_а0. Резистор R₁, как правило, обладает высокоомным сопротивлением, очень большим по сравнению с R. Величина же последнего выбирается из условия обеспечения достаточно широкой полосы пропускания усилителя. Схема замещения анодной цепи усилителя представлена на рис. 5.15, б.

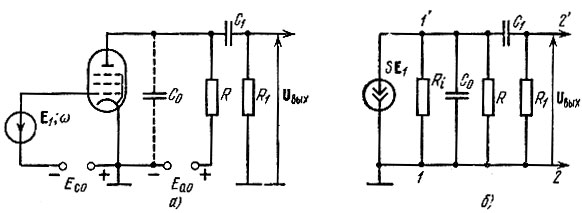
Рис. 5.15. апериодический ламповый усилитель с разделительной цепью R₁C₁ на выходе (а) и схема замещения анодной цепи (б)

Определим сначала напряжение на зажимах 1-1' (рис. 5.15, б), создаваемое током SΕ₁; очевидно, что

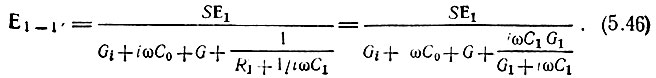
Тогда напряжение на выходе усилителя (зажимы 2-2')

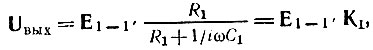
где

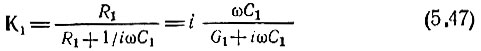
- передаточная функция разделительной цепи R₁, C₁.

На основании выражений (5.46) и (5.47) получаем

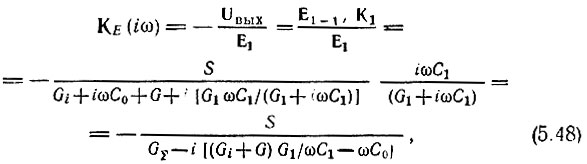
где 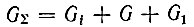(слагаемое G₁C₀/C₁ отброшено ввиду того, что С₀/С₁ << 1).

Рассмотрим частотную характеристику усилителя, На участке, примыкающем к ω = 0, т. е. при частотах, на которых сопротивление разделительного конденсатора 1/ωС₁ больше или, соизмеримо с сопротивлением R₁, влиянием проводимости iωС₀, а также проводимости 1/(R₁ + 1/iωC₁) в (5.46) можно пренебречь, благодаря чему выражение (5.48) принимает вид

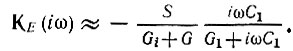
Модуль этого выражения

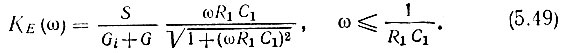
На среднем участке характеристики, на частотах, при которых а проводимость ωС₀ все еще пренебрежимо мала по сравнению с проводимостью G, формула (5.49) еще более упрощается:

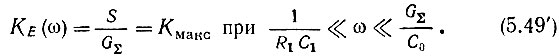
Наконец, при относительно высоких частотах, когда проводимость ωС₀ соизмерима с G_Σ, получается

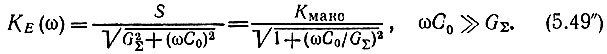
При изменении частоты со получаем частотную характеристику, изображенную на рис. 5.16, а.

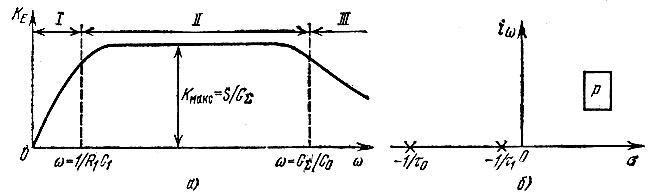
Рис. 5.16. Частотная характеристика (а) усилителя, показанного на рис. 5.15, и полюса его передаточной функции (б)

Обычно выполняются следующие неравенства: 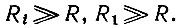Поэтому можно пренебречь проводимостями G_i и G₁ по сравнению с G, что позволяет считать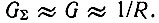

При этом выражение (5.48) упрощается:

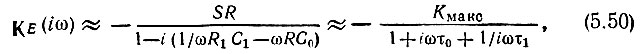
где τ₀ = RC₀ - постоянная времени цепи R, С₀; τ₁ = R₁C₁ - постоянная времени разделительной цепи R₁, С₁;

- коэффициент усиления (приближенное значение) в области частот 1/R₁C1 < ω < 1/RC₀.

Переходя к комплексной переменной р = σ + iω, запишем выражение (5.50) в форме

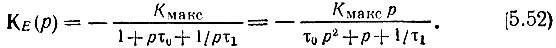
Полюса передаточной функции Κ(р) (корни уравнения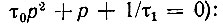

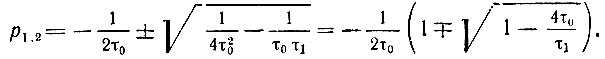
Так как то

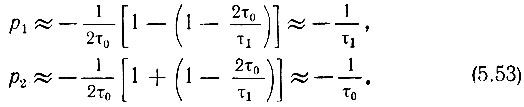
Расположение полюсов р₁ и р₂ на плоскости р показано на рис. 5.16, б.

Заметим, что при С₁ → ∞ (при конечном и неизменном R₁) формула (5.48) переходит в

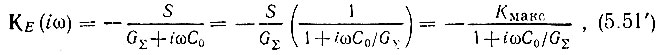
совпадающую с (5.43) при замене в последней G_i + G на G_Σ. При этом полюс (единственный) передаточной функции

будет в точке р₁ = -G_Σ/C₀.

Соотношения (5.44)-(5.53) будут использованы в следующей главе при анализе прохождения сигналов через апериодический усилитель. Там же определим импульсную характеристику рассматриваемого усилителя.