5.8. Обратная связь в активном четырехполюснике

При анализе линейных усилителей в § 5.4-5.7 на базе матриц параметров эквивалентных четырехполюсников основное внимание уделялось параметрам Y₂₁, Z₂₁, H₂₁, поскольку именно эти параметры определяют усилительную способность активного четырехполюсника. В реальных, не полностью однонаправленных активных четырехполюсниках приходится считаться с воздействием выходного колебания на вход усилителя.

Пусть в рабочем режиме усилителя, представленного на рис. 5.19, напряжение и ток на выходе будут Е₂ и I₂. Рассматривая теперь эти величины как результат внешнего воздействия со стороны выхода, можно определить I'₁ и Е'₁ на входе с помощью схемы замещения (рис. 5.19).

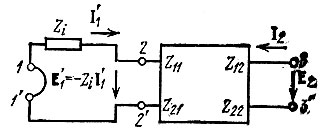
Рис. 5.19. К учету обратной реакции в усилителе

На этой схеме зажимы 1-1', к которым подключен входной источник сигнала, условно замкнуты накоротко, а под напряжением, действующим на зажимах 2-2', подразумевается Е'₁ = -Z_iI'₁, т. е. падение напряжения на внутреннем сопротивлении источника Z_i, создаваемое током I'₁.

Уравнения (5.4) при обозначениях рис. 5.19 записываются в форме

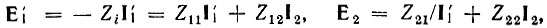
откуда нетрудно получить соотношение

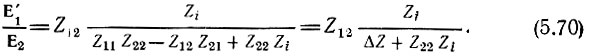
Напряжение Е'₁ часто называют напряжением обратной реакции или напряжением обратной связи. Элементом обратной связи является Z₁₂. При представлении эквивалентной схемы четырехполюсника с помощью Y-или H-матрицы элементами обратной связи являются соответственно параметры Y₁₂ и Н₁₂.

Рассмотренную обратную связь, обусловленную физическими параметрами усилительного прибора, можно назвать внутренней обратной связью. Как правило, она приводит к нежелательным явлениям - зависимости параметров входной цепи усилителя от элементов нагрузки, к опасности нарушения устойчивости при некоторых условиях и т. д.

Рассмотрим основные понятия, касающиеся применения в усилителях внешней обратной связи. Наиболее простым способом ее осуществления является соединение выхода усилителя со входом при помощи двухполюсника (рис. 5.20).

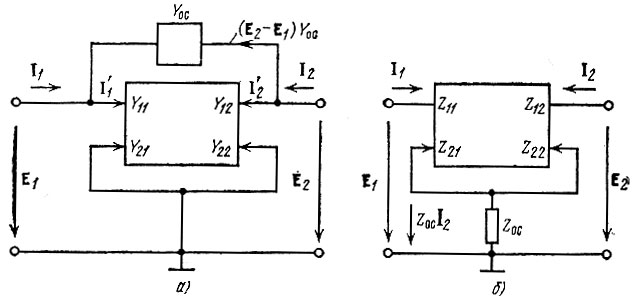
Рис. 5.20. Схема усилителей с обратной связью: а - по напряжению; б - по току

При соединении выхода со входом с помощью двухполюсника обратной связи Y_ос по схеме на рис. 5.20, а основной четырехполюсник целесообразно описывать с помощью Y-матрицы. Учитывая очевидные равенства 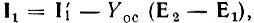а также соотношения между 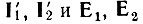в виде уравнений (5.1), приходим к новой системе уравнений

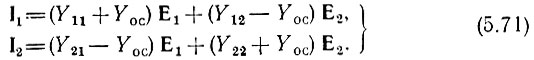
Таким образом, четырехполюснику с обратной связью по схеме на рис. 5.20, а соответствует матрица проводимостей

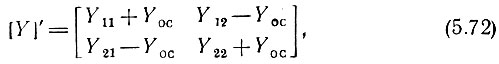
из которой следует, что подключение двухполюсника Y_ОС изменяет все элементы матрицы, в том числе и элемент обратной связи (Y₁₂ - Y_ОС вместо Y₁₂).

Аналогичным образом можно показать, что включение двухполюсника Z_ОС по схеме на рис. 5.20, б приводит к матрице

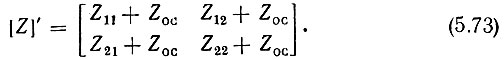
В схеме на рис. 5.20, а дополнительный ток, поступающий с выхода на вход по цепи обратной связи, равен (Е₂ - Е₁) Y_ОС; так как в усилителях обычно Е₂ >> Е₁, то величина этого тока приближенно равна Е₂Y_ОС, т. е. пропорциональна выходному напряжению. Поэтому схему на рис. 5.20, а можно называть схемой с обратной связью по напряжению. В схеме на рис. 5.20, б, в которой напряжение обратной связи пропорционально выходному току, осуществляется обратная связь по току. Можно, очевидно, осуществить комбинированную обратную связь - по напряжению и по току одновременно.

Различают два вида обратной связи: отрицательную и положительную.

Если введение обратной связи увеличивает коэффициент усиления цепи (по модулю), то обратная связь положительна, в противном случае - отрицательна.

Поясним применение выражений (5.71), (5.72) для схемы транзисторного усилителя с общим эмиттером при Y_ОС = 1/R_ОС (рис. 5.21).

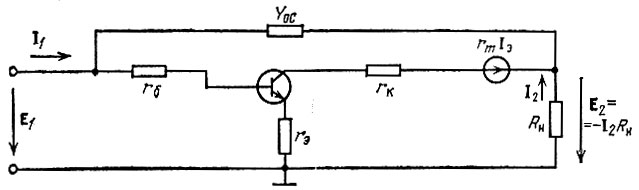
Рис. 5.21. Пример схемы замещения усилителя ОЭ с внешней обратной связью

Основываясь на формуле (5.17), в которой Y₂₁ заменяем величиной Y₂₁ - Y_ОС, а Y₂₂ - величиной Y₂₂ + Y_ОС [см. (5.72)], определяем коэффициент усиления напряжения выражением

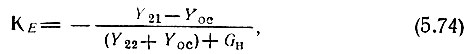
в которое подставим параметры Y₂₁ и Y₂₂, выраженные через параметры транзистора h_21э, r_б, r_э, r_к (см. § 5.4):

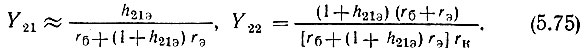
Обе эти проводимости - вещественные и положительные величины. То же самое относится и к Y_ОС = 1/R_ОС, G_H = 1/R_H. Очевидно, что вычитание из числителя и добавление к знаменателю дроби в (5.74) Y_ОС приводит к уменьшению коэффициента усиления (по модулю), т. е. в рассматриваемом случае обратная связь отрицательна. Это объясняется противофазностью выходного и входного напряжений в резистивной схеме с общим эмиттером (см. § 5.4); ток через R_ОС, направленный с выхода на вход (≈ Е₂/R_ОС = -I₂R_H/R_ОС), уменьшает ток I_б и, следовательно, Е₂.

Можно показать, что аналогичное подключение двухполюсника Y_ОС = 1/R_ОС к усилителю, работающему по схеме с общей базой, когда напряжения Е₂ и Е₁ совпадают по фазе, приводит к положительной обратной связи.

На рис. 5.22 изображена структурная схема усилителя с внешней обратной связью по напряжению, осуществляемой с помощью вспомогательного четырехполюсника К_ОС (iω).

Как усилитель К_у(iω), так и четырехполюсник К_ОС(iω) предполагаются полностью однонаправленными. Подобное представление имеет смысл в тех случаях, когда входное сопротивление четырехполюсника К_ОС(iω) достаточно велико, чтобы не нагружать усилитель К_у(iω); выходное сопротивление четырехполюсника К_ОС(iω) должно быть достаточно малым по сравнению с входным сопротивлением усилителя К_у(iω). При этих допущениях передаточную функцию системы в целом

можно найти с помощью следующих очевидных соотношений. Напряжение на выходе четырехполюсника обратной связи

Напряжение на входе усилителя К_у(iω) равно сумме входной э. д. с. Е и напряжения обратной связи U_ОС.

Следовательно, напряжение на выходе всей цепи

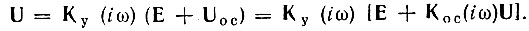
Решая это уравнение относительно U, получаем

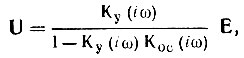
откуда следует, что

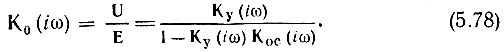
Это выражение является основным для системы с обратной связью. К₀(iω) иногда называют общей передаточной функцией, или предаточной функцией замкнутой системы. Произведение же К_у(iω)К_ОС(iω), имеющее смысл передаточной функции каскадного соединения четырехполюсников К_у(iω) и К_ОС(iω), называют передаточной функцией разомкнутой системы.

При замене iω на р получаем операторную форму передаточной функции замкнутой цепи

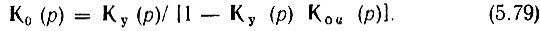
Сопоставление К_О(iω) с К_у(iω) позволяет определить знак обратной связи в общем случае, когда эти функции являются комплексными. Если на какой-нибудь частоте имеет место неравенство К_О(ω) < К_у(ω), т. е. если введение обратной связи приводит к уменьшению усиления, то обратная связь на данной частоте отрицательна, в противном случае - положительна.

При К_у(iω)К_ОС(iω) = 1 усиление К₀(iω) становится бесконечно большим. Это означает, что цепь становится неустойчивой и для исследования ее поведения необходимо использовать другие методы, так как. выражения (5.67)-(5.78), относящиеся к стационарным режимам, теряют свой смысл.

Случай неустойчивого состояния покоя (при изучении свойств автоколебательных систем) рассматривается в гл. 9. В данной главе изучаются только устойчивые цепи. Условия устойчивости будут сформулированы в § 5.10 после изложения основ теории устойчивости линейных цепей с обратной связью.