5.11. Частотные критерии устойчивости

Требование, чтобы передаточная функция

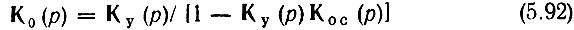
не имела полюсов в правой полуплоскости р = σ + iω, т. е. в области, ограниченной полуокружностью бесконечно большого радиуса R и осью iω (рис. 5.28, а), равносильно^* условию, что знаменатель выражения (5.92) не должен иметь нулей в указанной области или, что то же самое, функция

^* (Предполагается, что прямой усилитель устойчив, т. е. К_у(р) не имеет полюсов в правой полуплоскости р.)

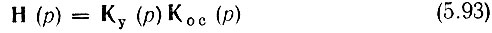
не должна обращаться в единицу ни в одной из точек правой полуплоскости р. Но Н(р) представляет собой передаточную функцию разомкнутого кольца обратной связи, т. е. отношение напряжения на зажимах 2-2 к напряжению на зажимах 1-1 при разомкнутом кольце, как это показано на рис. 5.29. Следовательно, об устойчивости системы с обратной связью можно судить по характеристикам разомкнутого тракта.

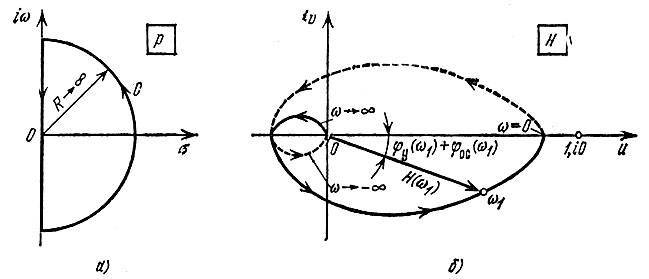
Рис. 5.28. Замкнутый контур на р-плоскости (а) и годограф функции Н(iω) на плоскости u+iv (б)

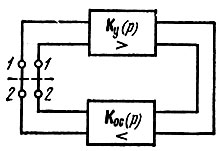
Рис. 5.29. К определению передаточной функции разомкнутого тракта усилитель - четырехполюсник обратной связи

Для дальнейшего анализа целесообразно перейти от плоскости р = σ + iω к плоскости Н(р) = u + iv (рис. 5.28, б).

Каждой точке р из плоскости σ, iω соответствует определенное значение Н на плоскости u, iv. Любой замкнутый контур на плоскости р преобразуется с помощью выражения (5.93) в некоторый (также замкнутый) контур на плоскости Н.

Если исходный контур на плоскости р задан в виде контура на рис. 5.28, а, соответствующий ему контур на плоскости Н называется годографом функции Н.

Показанный на рис. 5.28, а контур С можно разбить на два участка: 1) прямая iω при изменении ω от ∞ до -∞ и 2) полуокружность бесконечно большого радиуса R.

На первом участке, где σ = 0, р = iω, функция Н(р) обращается в функцию Н(iω). В соответствии с выражением (5.93) этот участок преобразуется на плоскости Н в линию, определяемую следующим соотношением:

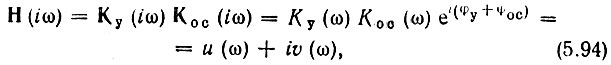
откуда

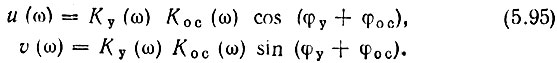
В этих выражениях φ_у и φ_ос - аргументы передаточных функций соответственно четырехполюсников К_у(iω) и К_ОС(ω).

На втором участке контура С (рис. 5.28, а) при R → ∞ функция^*Н(р) → 0. Это вытекает из общего выражения (5.87), которое можно записать в форме

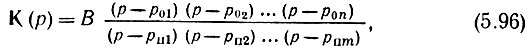
^* (имеются в виду наиболее распространенные в практике четырехполюсники с передаточной функцией, у которой степень числителя n меньше степени знаменателя m.)

где В - постоянный коэффициент, а p_oi и p_пj - соответственно нули и полюса функции К(р). При |р| → ∞ величинами p_oi и p_пj можно пренебречь и функцию К(р) можно представить в виде Вр^(n-m). Совершенно аналогично и функцию Н(р) при р → ∞ можно представить в форме

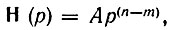
где n и m - числа соответственно [нулей и полюсов функции Н(р).

При n < m и |р| → ∞ модуль функции Н(р) на полуокружности R → ∞ равен нулю. Таким образом, полуокружность бесконечно большого радиуса R на плоскости р преобразуется в точку, лежащую в начале координат на плоскости Н, и для построения годографа Н в виде замкнутого контура достаточно знать поведение Н(р) на оси iω, т. е. знать амплитудно-частотную и фазочастотную характеристики цепи К_у(iω) К_ос(iω).

Обходу контура С в положительном направлении (против часовой стрелки) соответствует обход годографа Н при изменении частоты от ∞ до -∞.

Вся правая полуплоскость р преобразуется на плоскости Н во внутреннюю область годографа. Следовательно, если годограф передаточной функции разомкнутого тракта не охватывает точку 1, i0, то при замкнутой цепи обратной связи система устойчива, в противном случае система неустойчива.

Это условие называется критерием устойчивости Найквиста.

Показанная на рис. 5.28, б диаграмма соответствует устойчивой системе. Это видно из того, что годограф Н не охватывает точку 1, i0. Сплошной линией показана часть контура, соответствующая положительным частотам 0 > ω > ∞, а штриховой кривой - отрицательным частотам. Так как функция u(ω) четная, а v(ω) нечетная относительно со, то оба участка годографа симметричны относительно действительной оси.

Следует также отметить, что рис. 5.28, б построен для случая, когда при ω = 0 передаточная функция Н(iω) отлична от нуля (это возможно, например, для усилителей постоянного тока, в которых отсутствуют разделительные конденсаторы).

При сложной схеме цепи форма годографа иногда бывает настолько усложненной, что по ней трудно судить о том, охватывается или не охватывается годографом точка 1, i0. В подобных случаях оказывается полезным критерий, вытекающий из критерия Найквиста, основанный на подсчете числа пересечений оси u(ω) на участке 1, ∞. Для устойчивости цепи необходимо, чтобы годограф либо вообще не пересекал этот отрезок (как на рис. 5.28, б), либо пересекал его в положительном и отрицательном направлениях одинаковое число раз.

Критерий Найквиста получил наибольшее распространение в радиоэлектронике, автоматике и других смежных областях. Основное его преимущество: удобство оперирования с амплитудно-частотной и фазочастотной характеристиками разомкнутой цепи. В некоторых системах, например, содержащих линии, этот метод по существу является единственно приемлемым.

Вместо полярных диаграмм (годографов), изображенных на рис. 5.38, при применении критерия Найквиста можно использовать обычные амплитудно-частотную и фазочастотную характеристики разомкнутой цепи.

Действительно, длина вектора Н(iω), как это ясно из выражения (5.94), есть не что иное, как модуль коэффициента передачи разомкнутой цепи К_уК_ОС, т. е. частотная характеристика этой цепи, а аргумент φ_Н (рис. 5.30), равный

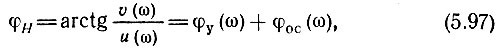
есть фазовая характеристика цепи К_уК_ОС.

Совместив на общем графике амплитудно-частотную и фазовую характеристики, нетрудно ответить на вопрос об устойчивости цепи.

Если при изменении ω от 0 до ∞ фаза φ_Н и не достигает величины n 2π, где n - целое число, то замкнутая цепь устойчива при любой величине К_уК_ОС. С другой стороны, если К_уК_ОС при любой частоте меньше единицы, то цепь устойчива при любой фазовой характеристике. Цепь неустойчива, если имеются частоты, при которых одновременно выполняются два условия:

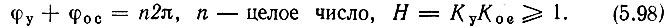
По существу эти два условия необходимы для обращения в нуль знаменателя в выражении (5.78), определяющем передаточную функцию замкнутой цепи.

Пример амплитудно-частотной и фазовой характеристик устойчивой цепи с обратной связью показан на рис. 5.30, а неустойчивой - на рис. 5.31. В первом случае (рис. 5.30) на частоте ω₀, соответствующей φ_у + φ_ос = 2π, модуль Н < 1. Во втором же случае (рис. 5.31) ω_г - частота паразитной генерации, На рис. 5.30 и 5.31 отложены абсолютные значения φ_у + φ_ос. При учете знака реальных φ_у и φ_ос наклон фазовых характеристик будет отрицательным.

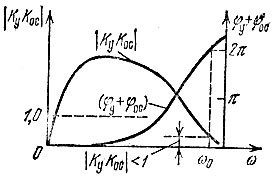
Рис. 5.30. Пример АЧХ и ФЧХ устойчивого усилителя с обратной связью

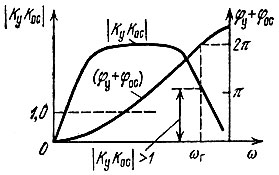
Рис. 5.31. То же для неустойчивого усилителя

При построении этих характеристик учтено, что при ω = 0 и ω = ∞ величина К_уК_ОС обращается в нуль. При ω → 0 это обусловлено влиянием последовательно включенных конденсаторов в канале К_у или К_ОС, а при ω → ∞ - влиянием шунтирующих емкостей (межэлектродные емкости, емкость монтажа и т. д.). Полное изменение фазы при изменении ω от 0 до ∞ зависит от характера и числа звеньев в усилителе и в цепи обратной связи.