6.2. Спектральный метод

В основе этого метода лежит использование введенной в предыдущей главе передаточной функции цепи К(iω) (см. § 5.3).

Если на входе линейного четырехполюсника действует сигнал произвольной формы в виде э. д. с. е(t), то, применяя спектральный метод, следует определить спектральную плотность входного сигнала Е(ω). Эта операция легко осуществляется с помощью выражения (2.38). Умножением Е(ω) на К(iω) получаем спектральную плотность сигнала на выходе четырехполюсника. Наконец, применяя к произведению Е(ω) К(iω) обратное преобразование Фурье [см. выражение (2.49)], определяем выходной сигнал в виде функции времени.

Таким образом, если входной сигнал записан в виде интеграла

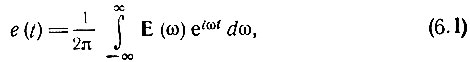
то выходной сигнал можно представить в аналогичной форме

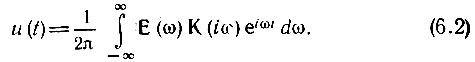
Сравнение выражения (6.2) с (6.1) показывает, что сигнал на выходе линейной цепи можно получить суммированием спектра Е(ω) входного сигнала с весом К(iω). Иными словами, передаточная функция цепи К(iω) является весовой функцией, определяющей относительный вклад различных составляющих спектра Е(ω) в сигнал u(t).

В § 2.13 отмечалось, что анализ переходных процессов значительно упрощается при представлении как внешней силы, так и передаточной функции цепи в виде преобразований Лапласа. При этом обозначение передаточной функции можно сохранить прежним, а изменить только аргумент, так что К(iω) перейдет в К(р). Функция же Е(ω) переходит в L_e(р) (см. § 2.13). Для упрощения записи преобразование Лапласа от функции времени е(t) в дальнейшем обозначается символом Е¯(р). При этом выражение (6.2) приводится к виду [см. § 2.13]

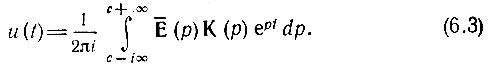
При t > 0 замкнутый контур интегрирования, образованный добавлением дуги бесконечно большого радиуса в левой полуплоскости (рис. 6.1), охватывает все полюса подынтегральной функции как Е¯(р), так и К(р), благодаря чему имеет место соотношение

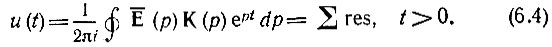
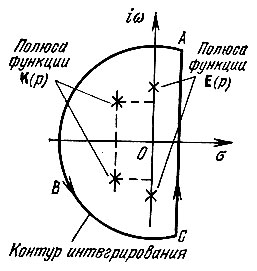
Рис. 6.1. Контур интегрирования при t > 0

Здесь Σ res - сумма вычетов в указанных полюсах.

При t < 0 контур интегрирования лежит в правой полуплоскости, не содержит полюсов и интеграл равен нулю.

Показанное на рис. 6.1 расположение полюсов функции Е¯(р) (на мнимой оси) соответствует э. д. с. вида е(t) = Е₀ cos ω₀t, существующей при t ≥ 0.

Итак, вычисление интеграла (6.4) сводится к определению вычетов в полюсах подынтегральной функции. Представим подынтегральную функцию выражения (6.4) в виде

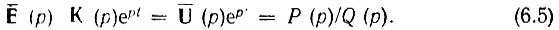
Тогда вычет функции Р(p)/Q(р), имеющей в точке р₁ простой полюс (первой кратности), определяется формулой

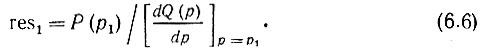
Если функция Р(p)/Q(р) имеет в точке р₁ полюс кратности m (m - целое положительное число), то

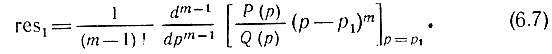
Методика применения контурных интегралов для определения некоторых функций, играющих большую роль в теории переходных процессов, будет в дальнейшем пояснена на примерах.