6.3. Метод интеграла наложения

Вместо разложения сложного сигнала на гармонические составляющие (спектральный метод) можно воспользоваться разбиением сигнала на достаточно короткие импульсы (рис. 6.2).

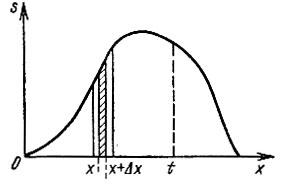
Рис. 6.2. Пояснение метода интеграла наложения

Если в основе спектрального метода лежит передаточная функция цепи К(iω), то метод интеграла наложения базируется на импульсной характеристике цепи g(t), введенной в § 5.3.

Пусть требуется найти сигнал s_вых(t) на выходе цепи, если задан сигнал s(t) на входе цепи и известна ее импульсная характеристика g(t). Для уяснения сути метода интеграла наложения поступим следующим образом. Разобьем произвольный сигнал s(x) на элементарные импульсы, как это показано на рис. 6.2, и найдем отклик цепи в момент t на элементарный импульс (на рис. 6.2 заштрихован), действующий на входе в момент x. Если бы площадь этого импульса равнялась единице, то импульс можно было бы рассматривать как дельта-функцию, возникшую в момент х. При импульсной характеристике цепи g(х) отклик в момент t был бы очевидно, равен g(t-х). Поскольку, однако, заштрихованная на рис. 6.2 площадь импульса равна s(х) Δх (а не единице), величина отклика в момент t будет s(х) Δxg (t-х).

Для определения полного значения выходного сигнала в момент t нужно просуммировать действие всех импульсов в промежутке от х = 0 до х = t. При Δх → 0 суммирование сводится к интегрированию.

Следовательно,

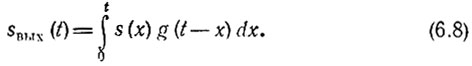
В общем случае, если начало сигнала s(х) не совпадает с началом отсчета времени х, последнее выражение можно записать в форме

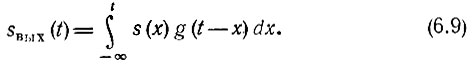
Для реальных цепей всегда выполняется условие

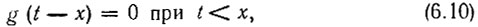
т. е. при отрицательном аргументе функция g(t-х) должна обращаться в нуль, так как отклик не может опережать воздействие. Поэтому выражение (6.8) можно заменить выражением

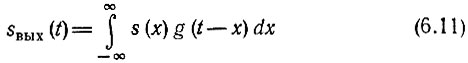
(при этом имеется в виду, что для х > t подынтегральное выражение обращается в нуль).

Приведем, наконец, еще одну форму записи, которая получается из выражения (6.8) при замене х на t - х:

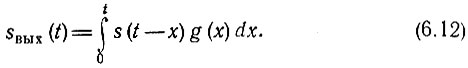
Интеграл, стоящий в правой части выражения (6.8), в математике называется сверткой функций s(t) и g(t) (см. § 2.7). Таким образом, приходим к следующему важному положению: сигнал s_вых(t) на выходе линейной цепи является сверткой входного сигнала s(t) с импульсной характеристикой цепи g(t).

Из выражения (6.11) видно, что сигнал на выходе цепи s_вых(t) в момент t получается суммированием мгновенных значений входного сигнала s(t) с весом g(t-х) за все предыдущее время.

В § 6.2 при суммировании спектра входного сигнала весовой функцией являлась передаточная функция цепи К(iω). В данном случае при суммировании мгновенных значений входного сигнала s(t) весовой функцией является импульсная характеристика цепи, взятая с аргументом (t-х), т. е. функция g(t-х).