6.4. Прохождение дискретных сигналов через апериодический усилитель

Дискретные сообщения обычно представляют собой последовательности импульсов. При передаче таких последовательностей через инерционные цепи форма импульсов претерпевает изменения, которые приводят к частичной или полной потере передаваемой информации. В связи с этим одной из наиболее типичных задач, с которыми сталкивается радиоинженер и исследователь в своей практической деятельности, является анализ искажения формы импульсов.

Из всего многообразия возможных форм импульсов наибольший интерес для анализа представляет прямоугольный импульс. Это связано с простотой формирования, а также с его широким применением в системах с двоичным кодом и во многих других радиотехнических устройствах. При работе с прямоугольными импульсами основное внимание обычно уделяется передаче фронта и среза импульса. Этот вопрос особенно важен, когда передаваемая или извлекаемая информация содержится в положении переднего (или заднего) перепада импульсов на оси времени (например, в некоторых радиолокационных системах).

Рассмотрим прохождение прямоугольного импульса через апериодический усилитель, изученный в § 5.6. Сначала рассмотрим схему с разделительной цепью R₁, С₁ (рис. 5.15, а). Передаточная функция этого усилителя определяется выражениями (5.50)-(5.52). Затем, положив С₁ → ∞, перейдем к схеме рис. 5.14, а характерной для транзисторного усилителя. Пусть в момент t = 0 на вход усилителя подается прямоугольный импульс э. д. с. е(t) с амплитудой Е и длительностью Т (рис. 6.3, а). На протяжении времени от t = 0 до t = Т напряжение на выходе усилителя можно рассматривать как результат включения при t = 0 постоянной э. д. с. e₁(t) = E. В момент t = Т включается дополнительная э. д. с. е₂(t) = -Е, компенсирующая первую э. д. с. (рис. 6.3, б). Суперпозиция выходных напряжений u₁(t) и u₂(t). обусловленных действием е₁(t) и е₂(t), образует импульс на выходе усилителя. Таким образом, задачу можно свести к рассмотрению процессов установления в усилителе при включении на входе постоянной э. д. с.

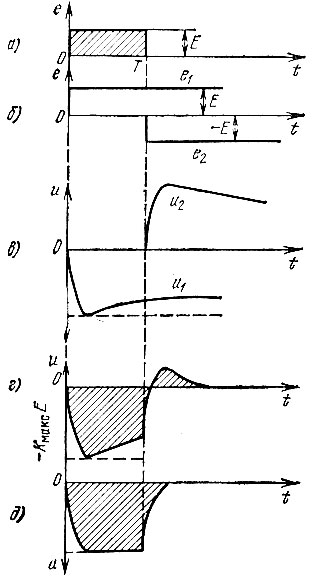
Рис. 6.3. Искажение формы импульса в резистивном усилителе: а - импульс на входе; б - представление импульса в виде суммы двух скачков; в - деформация скачков на выходе; г - результирующий импульс на выходе; д - импульс на выходе усилителя при устранении разделительной цепи R₁C₁

В соответствии с формулой (2.108) при включении в момент = 0 э. д. с. е₁(t) = E изображение

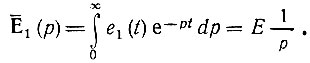
Тогда по формуле (6.3) выходное напряжение

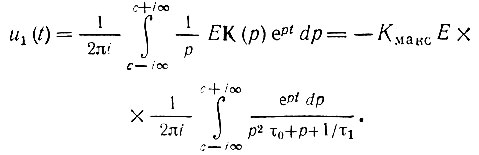
Полюса подынтегральной функции были определены в § 5.6 [см. формулы (5.53)]:

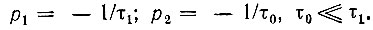
Находим вычеты по формуле (6.6)

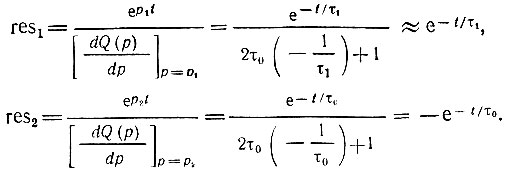
Итак,

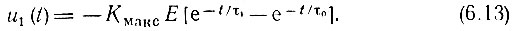
Графики u₁(t) и u₂(t) = -u₁(t - Т) изображены на рис. 6.3, в, а результирующее напряжение на выходе усилителя u(t) = u₁(t) + u₂(t) - на рис. 6.3, г.

Из формулы (6.13) и рис. 6.3, г видно, что при малых временах, т. е. при t, соизмеримых с τ₀, первая экспонента в выражении (6.13) близка к единице и основное влияние на фронт импульса оказывает вторая экспонента. Когда же t становится соизмеримым с τ₁, характер функции u₁(t) определяется в основном первой экспонентой. То же самое относится к функции u₂(t) при отсчете времени с момента t = T. Прямоугольный импульс с амплитудой K_максE, который имел бы место в идеальном усилителе с равномерной частотной характеристикой, изображен на рис. 6.3, г штриховой линией.

Искажение формы реального импульса проявляется: а) в конечной крутизне фронта и среза, б) в спаде вершины импульса.

Первый из этих факторов выражен тем сильнее, чем больше постоянная времени τ₀ = RC₀ (и, следовательно, чем сильнее завал частотной характеристики в области верхних частот).

Второй фактор (спад вершины импульса), наоборот, выражен тем сильнее, чем меньше постоянная времени τ₁ разделительной цепи R₁, С₁ (и, следовательно, чем сильнее завал частотной характеристики в области нижних частот).

Выбор постоянных времени τ₀ и τ₁ зависит от требований, предъявляемых к форме импульса на выходе усилителя. Если требуется, чтобы за время Т амплитуда достигала лишь своего максимально возможного значения K_максE, то постоянная времени τ₀ может иметь величину, близкую к Т. Форма импульса при этом далека от прямоугольной.

В тех случаях, когда требуется удовлетворительное воспроизведение формы импульса, постоянная времени τ₀ должна сопоставляться со временем, отводимым на длительность фронта выходного импульса, а постоянная времени τ₁ должна быть велика по сравнению с длительностью импульса Т. Этот результат имеет важное значение для правильного выбора параметров системы передачи дискретных сообщений, так как он указывает минимальное время, необходимое для перехода от одного дискретного уровня к другому.

Следует отметить, что в случае усиления импульсной последовательности проведенное выше рассмотрение справедливо при достаточно длительном интервале между импульсами, так что наложение переходных процессов от соседних импульсов не имеет места.

Продифференцировав (6.13) по t и приравняв Е к единице, получим выражение для импульсной характеристики апериодического усилителя

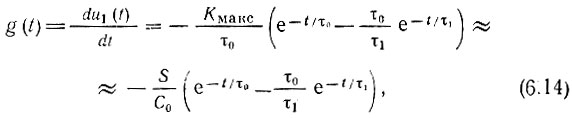
представленной на рис. 6.4, а.

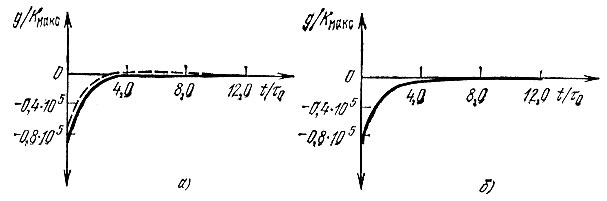
Рис. 6.4. Импульсная характеристика резистивного усилителя: а - с разделительной цепью R₁C₁ (^____τ₀ = 10^-5 c, τ₁ = 10^-2 c, τ₀/τ₁ = 10^-3; --- τ₀ = 10^-5 c, t = 10^-4 c, τ₀/τ₁ = 10^-1); б - без разделительной цепи)

Рассмотрим прохождение прямоугольного импульса через транзисторный апериодический усилитель, схема которого представлена на рис. 5.14, а. Как указывалось в § 5.6, для этого достаточно устремить емкость С₁ к бесконечности, т. е. закоротить конденсатор С₁, а проводимость G₁ = 1/R₁ включить в G. При этом формула (6.13) переходит в

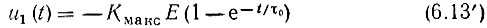
(так как τ₁ → ∞), а импульсная характеристика - в

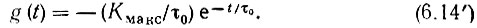
Импульс на выходе рассматриваемого усилителя изображен на рис. 6.3, д, а импульсная характеристика - на рис. 6.4, б.