6.5. Дифференцирование и интегрирование сигналов

В радиоэлектронике часто требуется осуществлять преобразование сигнала, имеющее характер дифференцирования или интегрирования.

На вход линейного устройства, осуществляющего дифференцирование, подается сигнал s(t); с выхода должен сниматься сигнал вида

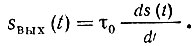
В интегрирующем устройстве связь между выходным s_вых(t) и входным s(t) сигналами должна иметь следующий вид:

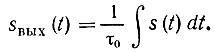
В этих выражениях τ₀ - постоянная величина, имеющая размерность времени.

Дифференцирование и интегрирование являются линейными математическими операциями. Следовательно, для дифференциального или интегрального преобразования сигнала следует применять линейные цепи и элементы, обладающие требуемыми соотношениями между входными и выходными величинами. Этим требованиям отвечают в принципе такие элементы, как обычные конденсаторы или катушки индуктивности в сочетании с резистором при надлежащем съеме выходного сигнала.

Рассмотрим сначала цепь, изображенную на рис. 6.5, а.

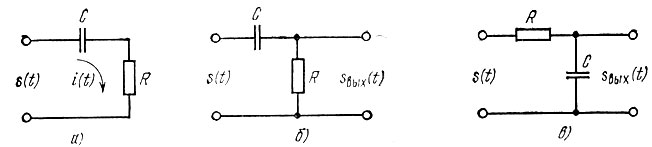
Рис. 6.5. Цепь, используемая для осуществления дифференцирования или интегрирования (а), дифференцирующая (б) и интегрирующая (в) RC-цепи

Подразумевая под входным сигналом s(t) электродвижущую силу, составим уравнение для тока в цепи i(t)

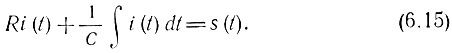
Умножим это уравнение на С и обозначим постоянную времени цепи τ₀ = RC. Тогда получим уравнение

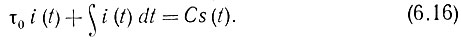
Характер функциональной связи между током i(t) и входным сигналом s(t) зависит от величины постоянной времени τ₀. Рассмотрим два крайних случая: очень малого и очень большого τ₀. В первом случае, т. е. при очень малом τ₀, первым слагаемым в левой части уравнения (6.16) можно пренебречь. Продифференцировав оставшееся после отбрасывания этого слагаемого уравнение по t, получим

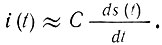
Отсюда видно, что напряжение на резисторе R, совпадающее по форме с i(t), пропорционально производной входного сигнала

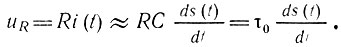
Таким образом, приходим к схеме дифференцирующего четырехполюсника, показанной на рис. 6.5, б, в которой выходной сигнал снимается с резистора R.

Во втором случае, т. е. при очень больших значениях τ₀, второе слагаемое в левой части уравнения (6.16) можно отбросить. При этом ток

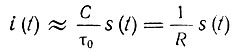
совпадает по форме с входным сигналом, а напряжение на конденсаторе С, равное

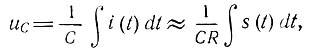
пропорционально интегралу от входного сигнала s(t). Отсюда следует, что для осуществления интегрирования RС-цепь должна быть использована в соответствии со схемой, показанной на рис. 6.5, в. Аналогичные результаты можно получить с помощью RL-цепи (рис. 6.6).

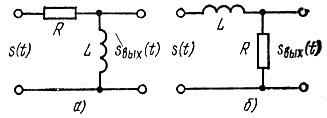
Рис. 6.6. Дифференцирующая (а) и интегрирующая (б) RL-цепи

В дифференцирующей цепи постоянная времени τ₀ = L/R должна быть достаточно мала, а в интегрирующей - достаточно велика. Принцип дифференцирования в первой схеме (рис. 6.6, а) можно представить следующим образом. При достаточно большой величине сопротивления R ток через RL-цепь почти не зависит от величины L и совпадает по форме с входным сигналом s(t). Выходной же сигнал s_вых(t) снимаемый с индуктивности L.

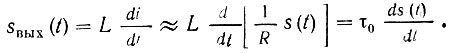
В схеме, показанной на рис. 6.6, б, наоборот, ток в основном определяется индуктивностью L (так как R весьма мало):

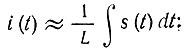
выходной же сигнал, снимаемый с резистора R,

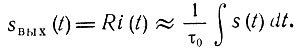
Уточним теперь использованные выше понятия "малое" и "большое" τ₀. Это проще всего сделать на основе спектрального рассмотрения. Если входной сигнал s(t) обладает спектральной плотностью S(ω), то при точном дифференцировании выходной сигнал 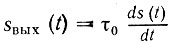должен обладать спектральной плотностью iωτ₀S(ω), а при точном интегрировании - плотностью (1/iωτ₀) S(ω) [см. выражения (2.59) и (2.60)]. Это означает, что для точного дифференцирования требуется четырехполюсник с коэффициентом передачи

а для точного интегрирования

Показанные на рис. 6.5, б и в четырехполюсники обладают передаточными функциями соответственно

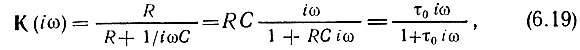
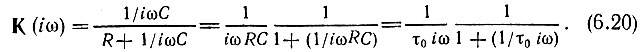
Из сравнения выражений (6.17) и (6.19) видно, что для удовлетворительного дифференцирования требуется, чтобы выполнялось условие

Это неравенство должно удовлетворяться для всех частот спектра входного сигнала, в том числе и для самой верхней.

Из сравнения же выражений (6.18) и (6.20) видно, что для удовлетворительного интегрирования требуется выполнение условия

Это неравенство должно удовлетворяться для всех частот спектра входного сигнала, в том числе и для самой нижней.

Из неравенств (6.21) и (6.22) следует, что при заданной цепи дифференцирование тем точнее, чем ниже частоты, на которых концентрируется энергия входного сигнала, а интегрирование тем точнее, чем выше эти частоты.

Из этих неравенств вытекает также следующее принципиальное положение: чем точнее дифференцирование или интегрирование, тем меньше (по модулю) передаточная функция К(iω) цепи, осуществляющей это преобразование сигнала. Сказанное относится к простейшим RC-или RL-цепям, представленным на рис. 6.5 и 6.6. В пределе, при идеальном преобразовании, К(ω) → 0.

Таким образом, простые RC- или RL-цепи пригодны лишь для приближенного дифференцирования сигналов. Точность дифференцирования можно в принципе повысить с помощью усилителя на выходе дифференцирующей цепи. Однако неизбежная нестабильность усиления и нелинейные искажения в простом усилителе делают такой способ практически неприемлемым. В связи с этим в прецизионных дифференцирующих устройствах применяют усилитель с отрицательной обратной связью по схеме, представленной на рис. 6.7, а.

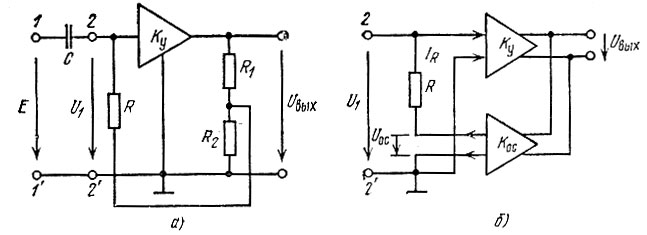
Рис. 6.7. Дифференцирующая цепь с применением отрицательной обратной связи (а) и схема замещения (б)

Напряжение обратной связи, снимаемое с резистора R₂, вводится в цепь резистора R. На рис. 6.7, б построена схема замещения для цепи, расположенной справа от зажимов 2-2'. Усилитель К_у, обладающий большим входным сопротивлением, рассматривается здесь как зависимый источник напряжения, управляемый напряжением. Четырехполюсник обратной связи соответствует делителю напряжения R₁, R₂; передаточная функция К_ОС = R₂/(R₁ + R₂).

Ток в цепи резистора R определяется очевидным выражением I_R = (U₁ - U_oc)/R. Учитывая, что U_ос = К_осU_вых и U_вых = К_уU₁, получаем

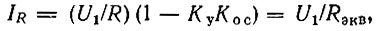
где R_экв = R/(1 - К_уК_ос) - эквивалентное сопротивление между зажимами 2-2'.

При отрицательной обратной связи выполняется условие К_уК_ос < 0. В рассматриваемой схеме К_ос - положительная (вещественная) величина, а К_у - отрицательная (например, при использовании транзисторного усилителя с общим эмиттером, см. § 5.4).

Таким образом, постоянная времени цепи С, R_экв, определяющая качество дифференцирования, будет

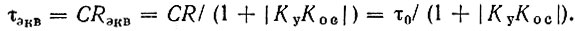
Передаточная же функция устройства в целом

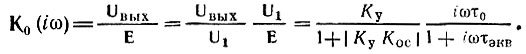
Так как величину τ_экв можно уменьшить во много раз по сравнению с τ₀, влияние слагаемого iωτ_экв в знаменателе второй дроби можно свести практически к нулю (без уменьшения модуля К₀(iω)). Так, например, при К_у = -100 и К_ос = 0,1, τ_экв = τ₀/(1 + 10) и К_уτ_экв = 100 τ₀/(1 + 10). В результате

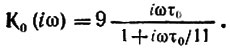
В современных прецизионных дифференцирующих устройствах применяются операционные усилители с очень большим усилением, позволяющие осуществить любое требуемое приближение передаточной функции к виду 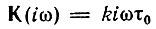(k - постоянный коэффициент).

В рассмотренной выше схеме (рис. 6.7, а) при 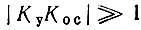передаточная функция

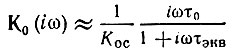
В заключение найдем импульсные характеристики дифференцирующей и интегрирующей цепей и приведем некоторые примеры прохождения импульсных сигналов через эти цепи. Проще всего определяется импульсная характеристика интегрирующей цепи.

Исходя из соотношения

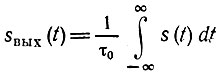
и подставляя вместо s(t) дельта-функцию δ(t), получаем для s_вых(t), т. е. в данном случае для импульсной характеристики идеального интегрирующего устройства, следующее выражение:

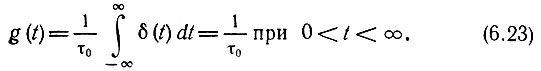
Единичный импульс и импульсная характеристика интегрирующей цепи изображены на рис. 6.8.

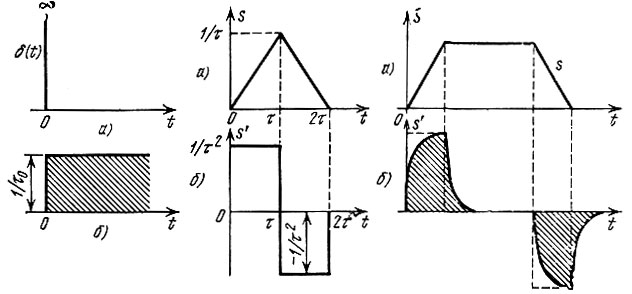
Слева: Рис. 6.8. Единичный импульс (а) и импульсная характеристика идеальной интегрирующей цепи (б). Рис. 6.9. К определению импульсной характеристики идеальной дифференцирующей цепи. Справа: Рис. 6.10. Сигнал на входе (а) и на выходе (б) дифференцирующей цепи

Для простой интегрирующей RС-цепи (рис. 6.5, в) импульсная характеристика

Нахождение импульсной характеристики дифференцирующей цепи затрудняется определением производной от дельта-функции. Это затруднение можно избежать, если короткий импульс, обращающийся в δ(t) при устремлении его длительности τ к нулю (см. § 2.11), продифференцировать до перехода к пределу. На рис. 6.9, а показан исходный импульс в виде треугольника с основанием 2τ и высотой 1/τ. Площадь импульса равна единице. Производная подобной функции изображена на рис. 6.9, б. При τ → 0 треугольный импульс обращается в дельта-функцию δ(t), а сдвоенный биполярный импульс (рис. 6.9, б) - в производную дельта-функции, т. е. в δ'(t).

Итак, импульсная характеристика идеального дифференцирующего устройства, получаемая из общего выражения s_вых(t) = τ₀s'(t) заменой s(t) на δ(t) и s_вых(t) на g(t), определяется выражением g(t) = τ₀δ'(t) при 0 < t < ∞. Она имеет вид, показанный на рис. 6.9, б при τ → 0.

Рис. 6.10 иллюстрирует прохождение трапецеидального импульса через дифференцирующую RС-цепь. Штриховыми линиями показан сигнал на выходе идеального дифференцирующего устройства.

На рис. 6.11 аналогичные построения сделаны для входного сигнала, представляющего собой прямоугольный импульс (рис. 6.11, а). При точном дифференцировании выходной сигнал должен представлять собой два единичных импульса: δ(t) и - δ(t - Т). В действительности же получаются два экспоненциальных импульса (на рис. 6.11, б заштрихованы).

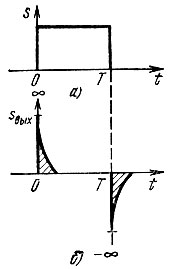
Рис. 6.11. Сигнал на входе (а) и выходе (б) дифференцирующей цепи

Приведенные на рис 6.10 и 6.11 примеры показывают, что чем медленнее во времени изменяется входной сигнал, тем лучше дифференцирование.

Рис. 6.12 иллюстрирует работу интегрирующей RС-цепи, когда на вход подан прямоугольный импульс. Чем больше постоянная времени цепи, тем ближе реальный выходной сигнал (сплошная линия) к идеальному (штриховая линия).

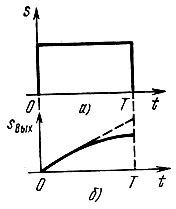
Рис. 6.12. Сигнал на входе (а) и выходе (б) интегрирующей цепи