6.6. Особенности анализа радиосигналов в избирательных цепях. Приближенный спектральный метод

Рассмотренные в предыдущей главе задачи характерны тем, что в них мы имели дело с сигналами, которые по своей форме совпадали с формой передаваемого сообщения. При передаче подобных сигналов задача сохранения информации тесно связана с задачей сохранения формы сигналов.

Иначе обстоит дело с радиосигналом, в котором информация заключена в одном из нескольких параметров высокочастотного колебания. Не обязательно сохранять полностью структуру этого колебания; достаточно лишь сохранить закон изменения того параметра, в котором заключена информация. Так, в случае амплитудно-модулированного колебания важно точно передать огибающую амплитуд, между тем как некоторое изменение частоты или фазы заполнения, не имеющее существенного значения, при анализе можно не учитывать. При передаче радиосигналов с угловой модуляцией, наоборот, основное внимание следует уделить точному воспроизведению закона изменения частоты и фазы.

Эти особенности радиосигналов открывают путь к некоторому упрощению методов анализа, их передачи через линейные цепи. Возможность упрощения особенно существенна, когда радиосигнал представляет собой узкополосный процесс, а цепь- узкополосную систему. Это как раз и характерно для реальных радиосигналов и реальных избирательных цепей. В § 3.1 уже отмечалось, что даже для "широкополосных" сигналов ширина спектра радиосигнала мала по сравнению с несущей частотой сигнала. Соответственно и полоса прозрачности цепи обычно мала по сравнению с ее резонансной частотой.

Спектральная плотность S_а(ω) высокочастотного модулированного колебания a(t) образует два всплеска вблизи частот ω₀ и - ω₀, а передаточная функция К(iω) - вблизи частот ω_р и - ω_р (рис. 6.13). Для общности здесь принято, что резонансная частота цепи сор не совпадает с центральной частотой сигнала ω₀, т. е. имеет место расстройка. При этом предполагается, что расстройка

является величиной того же порядка, что и полоса пропускания цепи.

Составим выражение для сигнала на выходе цепи. Если сигнал на входе цепи можно представить в форме a(t) = A(t) cos [ω₀t + θ(t)], выкладки значительно упростятся при использовании аналитического сигнала [см. § 3.10, формулы (3.87) и (3.88)]

Спектральная плотность [модуль Z(ω)] этого сигнала изображена на рис. 6.13 жирной линией (сравнить с рис. 3.25). Так как функция Z(ω) существует только в области положительных частот, то при определении аналитического сигнала на выходе цепи следует исходить из выражения

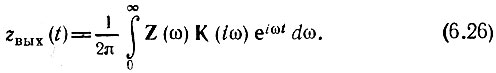
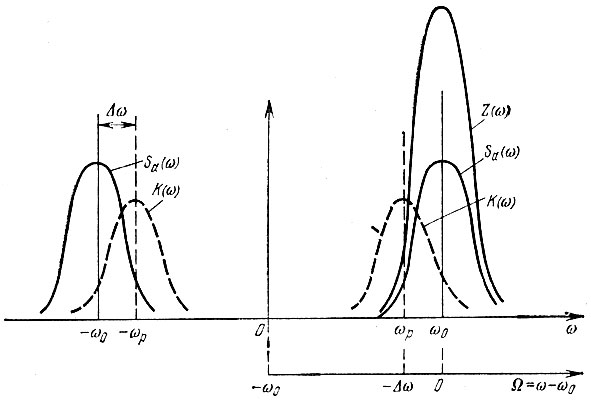
Рис. 6.13. Спектральная плотность модулированного колебания и передаточная функция узкополосной цепи

В § 3.10 было показано, что Z(ω) = 2S_а(ω) при ω > 0, причем в области положительных частот S_a(ω) = ¹/₂S_A(ω - ω₀) [см. формулу (3.10), выведенную для частного случая θ(t) = θ₀; при использовании комплексной огибающей последняя включает в себя θ(t.]

Следовательно, Z(ω) = S_A(ω - ω₀). Подставляя это выражение в (6.26), получаем

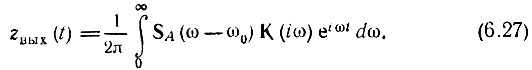
Перейдем к новой переменной Ω = ω - ω₀. Тогда:

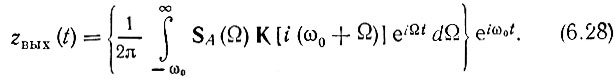
Из сопоставления этого выражения с (6.25) сразу видно, что выражение, стоящее в фигурных скобках, соответствует комплексной огибающей выходного колебания

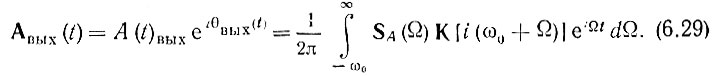
Дальнейшее упрощение анализа вытекает из свойств передаточной функции резонансных цепей, обладающих сильно выраженной частотной избирательностью. Модуль коэффициента передачи К(iω) быстро убывает при удалении ω от резонансной частоты.

Поэтому передаточную функцию целесообразно выражать в виде функции расстройки частоты ω относительно резонансной частоты ω_р:

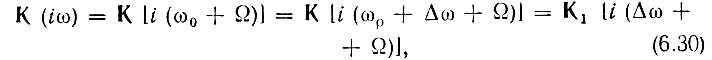
где постоянный параметр расстройки Δω = ω₀ - ω_р.

Так как при Ω = - ω₀ коэффициент передачи K₁[i(Δω + Ω)] практически равен нулю, нижний предел интеграла в выражении (6.29) можно заменить на -∞. При этом выражение (6.29) принимает следующий вид:

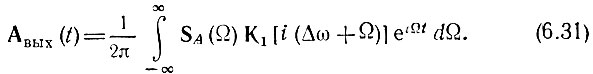
Это выражение ничем не отличается от обычного интеграла Фурье, определяющего оригинал по заданной спектральной плотности огибающей S_A(Ω) и передаточной функции K₁[i(Δω + Ω]).

Заменив iΩ на р, получим выражение в форме обратного преобразования Лапласа:

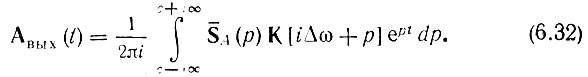
Таким образом, анализ передачи узкополосного высокочастотного колебания через избирательную цепь по существу сводится к анализу изменений, претерпеваемых комплексной огибающей входного сигнала. После нахождения A_вых(t) и θ_вых(t) для выходного сигнала (аналитического) можно написать следующее выражение:

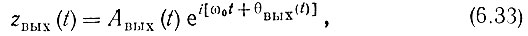
откуда

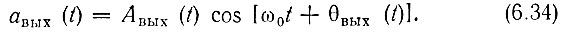
Вычисления, связанные с определением А_вых(t) по формуле (6.32), значительно проще, чем при непосредственном определении а_вых(t) с помощью обратного преобразования Лапласа, так как переход от S_a(ω) к S_A(Ω) и от К(р) к К₁(iΔω + р) сокращает число особых точек подынтегральной функции.