6.7. Упрощение метода интеграла наложения (метод огибающей)

В предыдущем параграфе упрощение спектрального метода достигалось упрощение передаточной функции избирательной цепи К(iω). Аналогично метод интеграла наложения можно упростить укорочением импульсной характеристики g(t), тесно связанной с передаточной функцией К(iω).

Основываясь на общем выражении (5.28)

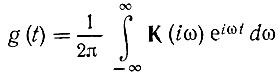
и переходя к аналитическому сигналу z_g(t), соответствующему физической функции g(t), можем написать [см. (3.91)]

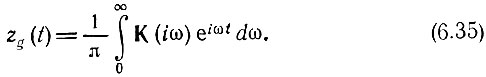
Как и в предыдущем параграфе, заменим переменную интегрирования ω = ω₀ + Ω. Тогда с учетом формулы (6.30) и после замены нижнего предела -ω₀ на -∞ получим

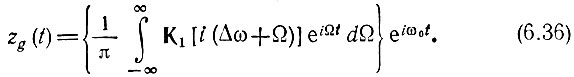
С другой стороны, представив искомую импульсную характеристику в форме

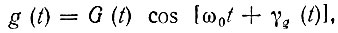
имеем

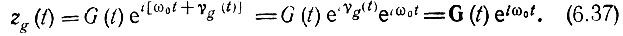
Из сравнения выражений (6.36) и (6.37) непосредственно вытекает равенство, определяющее комплексную огибающую импульсной характеристики g(t)

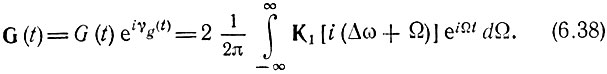
Как будет видно из приводимых далее примеров, применение этого выражения упрощает вычисление импульсной характеристики g(t).

Обращаясь теперь к выражению (6.31) и применяя правило (2.64), мы можем определить А_вых(t) в виде свертки двух функций времени, соответствующих спектральным функциям S_A(Ω) и К₁[i (Δω + Ω)].

Первой из этих спектральных функций соответствует А(t), а второй, как это следует из (6.38), - функция ¹/₂G(t).

Следовательно,

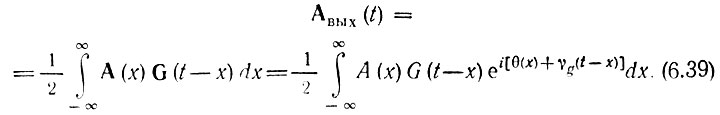
Это выражение является общим, пригодным для любых избирательных цепей и любых узкополосных сигналов. В тех случаях, когда свободные колебания характеризуются постоянной частотой заполнения, как, например, в одиночном контуре, γ_g(t) вырождается в постоянную фазу и выражение (6.39) существенно упрощается. То же самое относится и к сигналам с немодулированной частотой заполнения, когда θ(t) обращается в постоянную величину.

Метод интеграла наложения более эффективен в тех случаях, когда временные характеристики сигналов или цепей (или тех и других) оказываются более простыми, чем спектральные. Такое положение имеет место, в частности, при некоторых частотно-модулированных сигналах. Примеры применения метода огибающей приводятся в § 6.10.