6.8. Прохождение радиоимпульса через резонансный усилитель

Имея в виду радиоимпульс с прямоугольной огибающей и немодулированным высокочастотным заполнением, рассмотрим сначала явления в цепи при передаче фронта импульса, т. е. при включении в момент t = 0 гармонической э. д. с. е(t) = Е₀ cos (ω₀t + θ₀). В качестве выходной величины примем напряжение на колебательном контуре усилителя, схематически показанного на рис. 5.17.

Выведем сначала точное выражение для выходного напряжения.

Основываясь на общей формуле (5.60), домножим числитель и знаменатель входящей в нее дроби на iω/С:

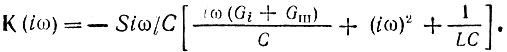
Воспользуемся известными соотношениями: 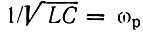- резонансная частота контура; 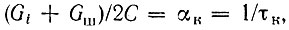где τ_к - постоянная времени контура; α_к - затухание.

Кроме того, воспользуемся выражением (5.61) для резонансного коэффициента усиления К_макс. Тогда передаточную функцию усилителя можно привести к виду

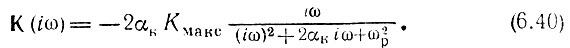
Таким образом, в операторной форме

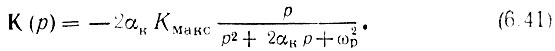
Изображение по Лапласу для колебания Е₀ cos (ω₀t + θ₀) имеет следующий вид:

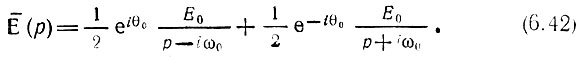
Напряжение на выходе усилителя [см. формулу (6.3)]

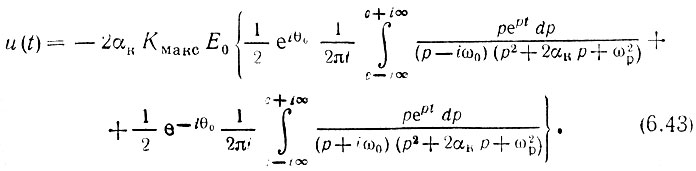
Вычислив вычеты в четырех полюсах, после весьма громоздких выкладок получим следующее окончательное выражение:

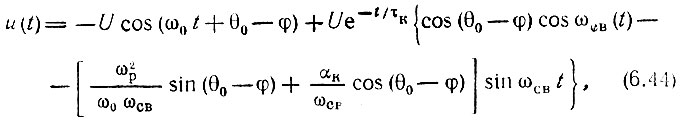
где 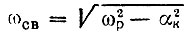- частота свободных колебаний, а φ = arctg (ω₀ - ω_р) τ_к - фазовый сдвиг (в стационарном режиме). Первое слагаемое в (6.44) определяет стационарное, а второе - свободное колебание.

Воспользуемся теперь приближенным выражением (6.32). Передаточную функцию определим по формуле (5.64), в которой под величиной а_экв в данном случае подразумеваем

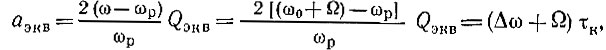
где 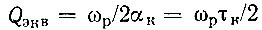- добротность контура с учетом проводимости G_i активного элемента.

Таким образом,

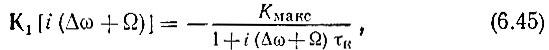
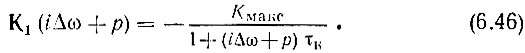
Составим теперь укороченное выражение для 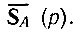В данном случае (при немодулированном высокочастотном заполнении), огибающая А(t) является вещественной функцией и имеет вид скачка Е₀. Спектральная плотность этой огибающей

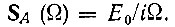
С учетом начальной фазы колебаний θ₀ спектральную плотность комплексной огибающей A(t) можно представить в форме

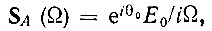
а ее изображение по Лапласу

Подставив формулы (6.46) и (6.47) в (6.32), определим комплексную огибающую на выходе усилителя

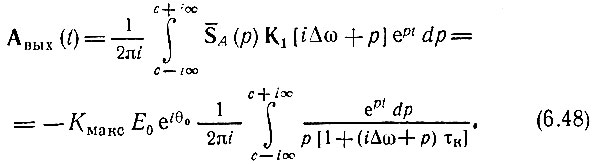
Подынтегральная функция имеет всего лишь два полюса

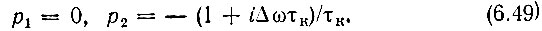
Вычеты в этих полюсах

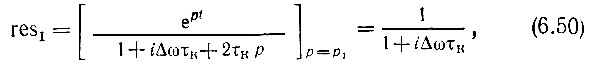
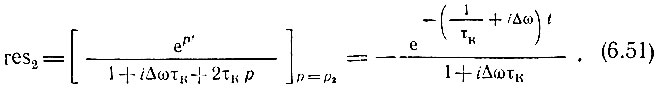
Таким образом, сумма вычетов

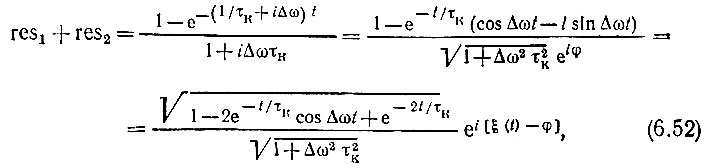
где

есть фазовый сдвиг напряжения на контуре относительно входной э. д. с. в стационарном режиме, а

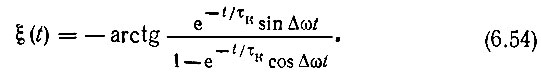
Итак, комплексная огибающая выходного напряжения

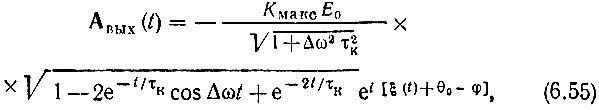
а мгновенное значение этого напряжения

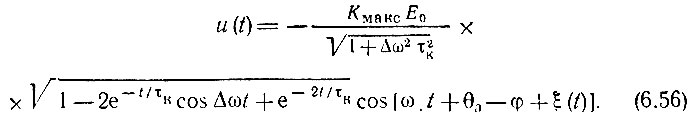
Для сравнения полученного результата с точным выражением (6.44) приведем u(t) к виду суммы двух колебаний - вынужденного и свободного. Для этого вернемся к формулам (6.48)-(6.55) и составим выражение для аналитического сигнала, соответствующего напряжению u(t):

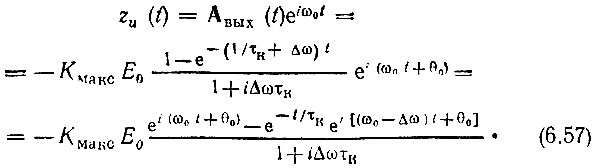
После приведения к тригонометрической форме с учетом соотношения (6.53), а также равенства ω₀ - Δω = ω_р получим

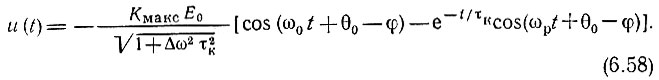
При 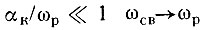и выражения (6.44) и (6.58) практически совпадают.

Рассмотрим важные для практики следствия, вытекающие из выражения (6.56). Остановимся сначала на случае точной настройки контура на частоту возбуждающей э. д. с. Приравнивая ω_р к частоте ω₀, получим Δω = 0. Тогда выражение (6.56) упрощается:

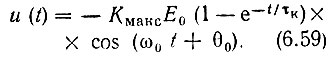
Из этого выражения видно, что при совпадении частот ω₀ и ω_р огибающая амплитуд выходного колебания нарастает по закону 1 - е^-t/τ_к независимо от фазы э. д. с. в момент включения.

Соответствующая этому случаю кривая, вычисленная по формуле

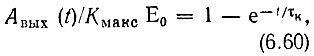
построена на рис. 6.14. На этом же рисунке приведены графики функции

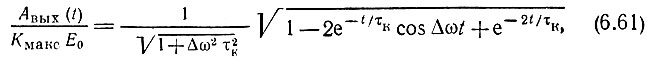
вычисленные для двух значений параметра расстройки Δωτ_к, равных 1 и 2.

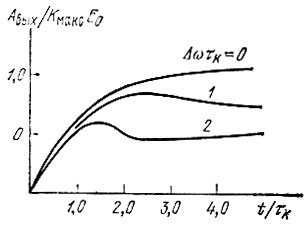
Рис. 6.14. Установление огибающей высокочастотного напряжения на выходе резонансного усилителя при включении гармонической э. д. с. при различных параметрах расстройки

Из рис. 6.14 видно, что при значительных расстройках процесс установления огибающей принимает колебательный характер. Это объясняется биением двух колебаний: частот ω₀ и ω_св. Последняя при сделанном выше допущении о высокой добротности контура очень мало отличается от резонансной частоты ω_р.

Из рис. 6.15, где приведены графики нормированной огибающей, т. е. функции 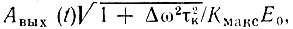видно, что с увеличением расстройки крутизна фронта огибающей растет и общая продолжительность процесса установления несколько сокращается. Графики функции ξ(t), т. е. переменной части θ_вых(t), приведены на рис. 6.16.

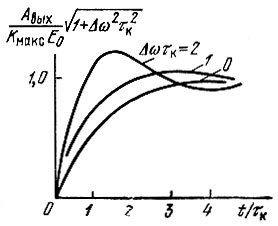
Рис. 6.15. То же, что на рис. 6.14, при нормировании огибающей относительно стационарного значения

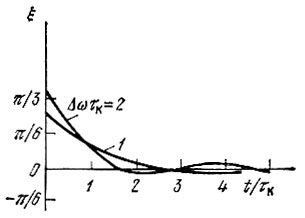
Рис. 6.16. Процесс установления фазы колебания в зависимости от параметра расстройки Δωτ_к

Используем полученные результаты для определения формы и параметров радиоимпульса на выходе одноконтурного усилителя при прямоугольной форме огибающей импульса на входе.

Колебание на входе (рис. 6.17, а), определяется выражением

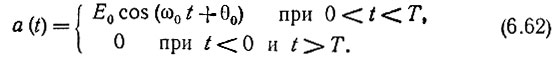
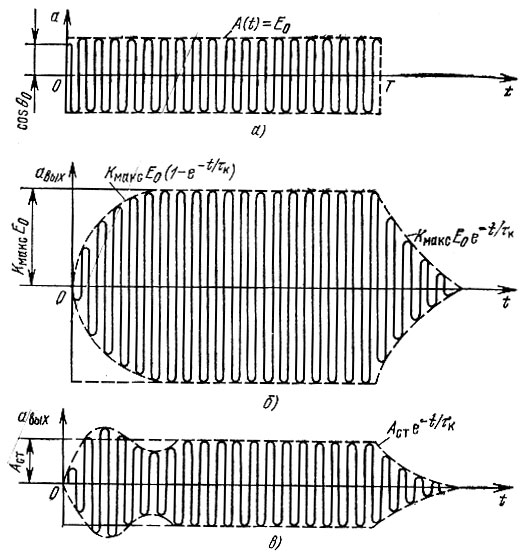
Рис. 6.17. Прохождение радиоимпульса через резонансный усилитель: а - импульс на входе усилителя; б - на выходе при точной настройке контура; в - на выходе при расстройке

Как и в § 6.4, задачу можно решить, рассматривая независимо явления на фронте и срезе импульса с последующей суперпозицией полученных решений.

Если длительность импульса t = Т больше, чем фактическое время установления режима в контуре при включении гармонической э. д. с., то к моменту окончания входного импульса на выходе усилителя амплитуда колебания будет равна стационарному значению

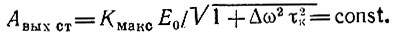
Начиная с момента t = Т, после прекращения действия внешней э. д. с., остается лишь свободное колебание, которое можно представить в форме

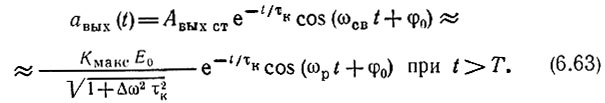
Здесь через φ₀ обозначена фаза напряжения на контуре в момент t = Т; ω_p ≈ ω_св.

Таким образом, в отличие от фронта на срезе импульса огибающая амплитуд имеет вид экспоненты независимо от соотношения частот ω₀ и ω_p. Сигнал на выходе усилителя при Δωτ_к = 0 и Δωτ_к = 2 (рис. 6.17, б и в) изображен для случая, когда длительность импульса значительно больше времени установления.