6.10. Прохождение фазоманипулированного колебания через резонансную цепь

Наряду с амплитудной модуляцией - непрерывной или импульсной - в радиотехнике находит применение фазовая манипуляция, заключающаяся в скачкообразном изменении фазы высокочастотного колебания на 180° в определенные моменты времени (рис. 6.21, а). Амплитуда и частота колебания поддерживаются при этом неизменными. На рис. 6.21, б фазы 0 и π чередуются периодически; при передаче реальных сигналов закон чередования может быть более сложным.

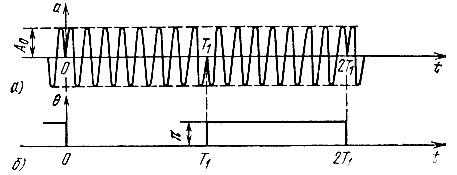
Рис. 6.21. Фазоманипулированное колебание (а) и характер изменения фазы (б)

Рассмотрим явления в резонансных цепях, возникающие в моменты скачкообразного изменения фазы входного сигнала. При этом будем считать, что тактовые интервалы Т₁ между двумя соседними скачками фазы намного больше длительности возникающих в цепи переходных процессов, так что рассмотрение каждого из скачков изолированно от предыдущих вполне допустимо.

Для выявления принципиальной стороны вопроса ограничимся простейшим случаем - передачей фазоманипулированного сигнала через одиночный колебательный контур, настроенный на частоту сигнала ω₀, т. е. ω₀ = ω_р.

Совместим начало отсчета времени с моментом скачка, как это показано на рис. 6.21. Тогда для t > 0 выходной сигнал на основании принципа суперпозиции можно представить в виде суммы свободного колебания, существующего после прекращения действия старого сигнала, и нарастающего колебания, обусловленного действием нового сигнала при t > 0, с фазой заполнения, на 180° отличающейся от фазы предыдущего сигнала.

Пренебрегая различием между собственной частотой контура ω_св и резонансной частотой ω_р, можем для двух упомянутых колебаний написать следующие выражения:

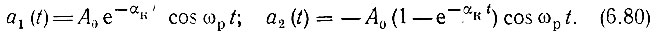
Знак минус в правой части второго выражения учитывает опрокидывание фазы на 180°.

Результирующий сигнал на выходе цепи (рис. 6.22)

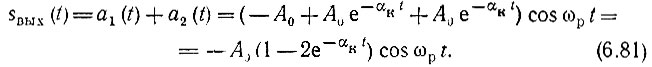
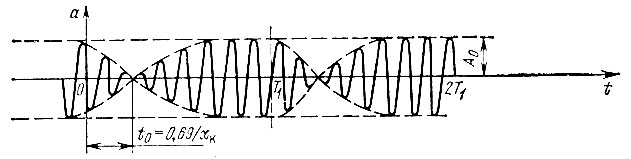
Рис. 6.22. Возникновение паразитной амплитудной модуляции в резонансном контуре при скачкообразном изменении фазы э. д. с

Из-за инерционности контура скачок фазы входного сигнала приводит к изменению амплитуды выходного сигнала. В момент времени t₀ = 0,69/α_к, при котором 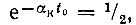огибающая обращается в нуль. Чем меньше α_к (или чем больше добротность контура), тем больше t₀, т. е. тем протяженнее процесс установления колебания с новой фазой.

В более сложных колебательных цепях, а также при наличии расстройки между частотами ω₀ и ω_p картина несколько усложняется: помимо возникновения паразитного изменения огибающей нарушается и характер изменения фазы. Вместо скачкообразного изменения получается плавный переход фазы от прежнего значения к новому. Способ определения структуры выходного сигнала остается прежним, только а₁(t) и а₂(t) в выражении для s_вых(t) будут представлять собой колебания с несовпадающими частотами. Вычислив модуль и аргумент суммарного колебания, нетрудно найти огибающую и фазу выходного сигнала.