6.11. Прохождение частотно-манипулированного колебания через избирательную цепь

Пусть сигнал на входе избирательной цепи имеет вид колебания, изображенного на рис. 6.23, а. В некоторые моменты времени частота скачком изменяется от ω₁ до ω₂ или от ω₂ до ω₁ при постоянной амплитуде и непрерывной фазе в моменты скачков частоты. Последнее допущение продиктовано желанием выяснить влияние на параметры выходного сигнала одной лишь манипуляции частоты, без наложения манипуляции фазы (рассмотренной в предыдущем параграфе).

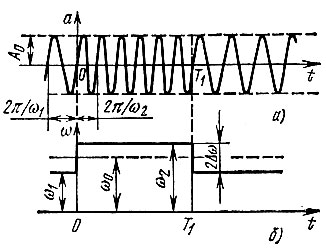
Рис. 6.23. Частотно-манипулированное колебание (а) и характер изменения частоты (б)

Совместим начало отсчета времени с моментом изменения частоты от ω₁ до ω₂ (рис. 6.23, б) и положим, как и в § 6.10, что к моменту t = 0 все процессы, связанные с предыдущим скачком частоты, уже закончены. Таким образом, при t < 0 выходной сигнал представляет собой гармоническое колебание с частотой ω₁ и постоянной амплитудой А₀.

На первый взгляд, может показаться, что изменение скачком одной лишь частоты входного сигнала при постоянстве амплитуды и отсутствии скачка фазы не должно сопровождаться переходными процессами. В действительности это не так, поскольку в цепях, запасающих энергию, переход от одной частоты к другой неизбежно связан с изменением запаса энергии.

Основная идея, на которой базируется дальнейшее рассмотрение, заключается в том, что мгновенное изменение частоты внешней э. д. с. эквивалентно выключению старой э. д. с. с частотой ω₁ и включению в тот же момент новой э. д. с. с частотой ω₂. Аналогичный прием был использован в § 6.10 для скачка фазы входного сигнала, однако в данном случае дело несколько осложняется несовпадением частот различных слагаемых.

Итак, результирующее колебание на выходе линейной цепи при t > 0

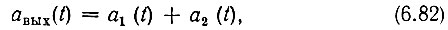
где а₁(t) - свободное колебание, связанное с выключением в момент t = 0 старой э. д. с. (частоты сох); а₂(t) - нарастающее колебание, обусловленное включением новой э. д. с. (частоты ω₂).

Рассмотрим одиночный колебательный контур при съеме выходного напряжения с емкости (рис. 6.24). Резонансную частоту контура сор приравняем частоте ω₀, а скачок частоты 2 Δω (см. рис. 6.23, б) будем считать симметричным относительно ω₀:

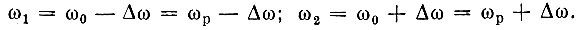
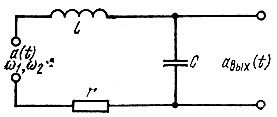
Рис. 6.24. Колебательный контур, возбуждаемый частотно-манипулированным колебанием

Тогда при обозначениях, принятых в § 6.8, и в соответствии со вторым слагаемым в выражении (6.58), при замене постоянного коэффициента - К_максЕ₀ на Q, свободное колебание можно представить следующим образом:

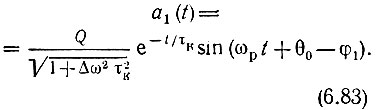
Заметим, что свободное колебание здесь взято со знаком плюс, поскольку речь идет не о включении новой, а о прекращении действия старой э. д. с. Косинус заменен на синус ввиду съема напряжения с емкости, входящей в последовательный контур. Кроме того, следует иметь в виду, что для частоты ω₁, которая ниже резонансной частоты контура, ток в контуре опережает по фазе э. д. с. и угол φ₁ является отрицательным, т. е.

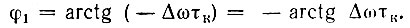
Таким образом, обозначив arctg Δωτ_к = φ, получим

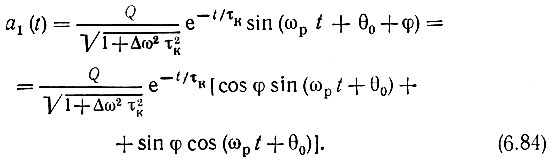
Для определения а₂(t) можно воспользоваться полным выражением типа (6.58), в котором постоянный коэффициент - К_макс × Е₀ следует заменить на Q, частоту ω₀ - на частоту новой э. д. с., т. е. на ω₂, косинусы должны быть заменены на синусы, а угол φ, как и в (6.84), следует определять выражением φ = Δωτ_к.

Итак,

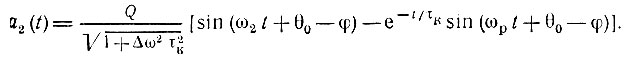
После подстановки 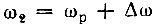это выражение приводится к виду

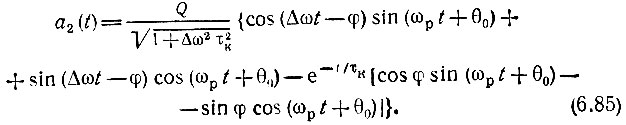
Просуммируем выражения (6.84) и (6.85):

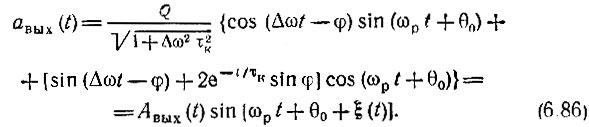
Огибающая А_вых(t) и переменная часть фазы ξ(t) выходного сигнала определяются выражениями

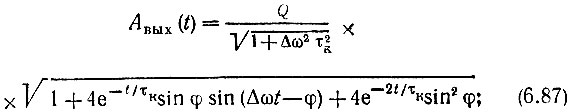
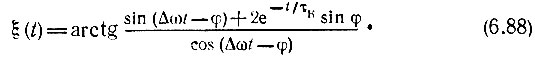
Основной интерес в данном случае представляет закон изменения частоты выходного колебания

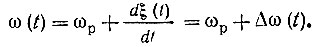
Выполнив дифференцирование, найдем

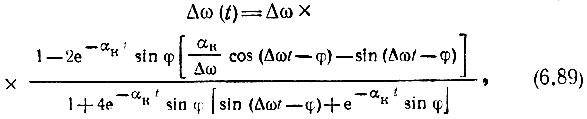
где α_к = 1/τ_к.

Выражение (6.89) можно упростить, так как

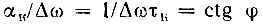
и числитель дроби приводится к виду

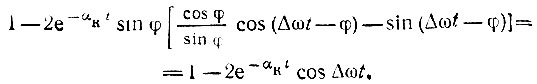
Итак, окончательно относительная расстройка

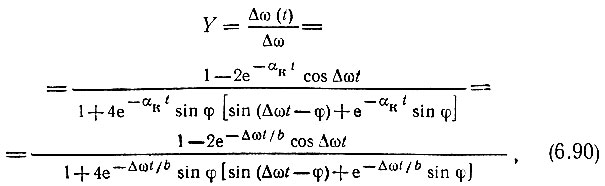
где b = Δω/α_к.

Графики Υ(Δωt) для нескольких значений параметра b построены на рис. 6.25. Заметим, что полоса пропускания контура, определяемая по ослаблению сигнала до 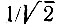от максимального значения, равна 2 α_к = ω_p/Q. Следовательно, параметр b есть не что иное, как отношение полного скачка частоты сигнала 2 Δω к полосе пропускания 2 α_к.

На рис. 6.26 в качестве независимой переменной выбрана величина α_кt, соответственно чему уравнение (6.90) принимает форму

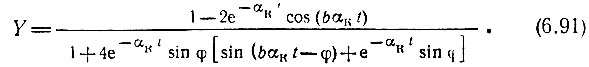
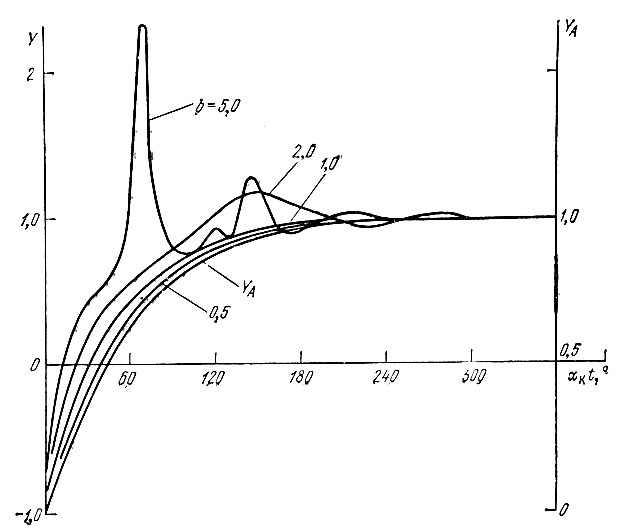
Рис. 6.26. То же, что на рис. 6.25 при безразмерном времени α_кt

При этом следует иметь в виду, что 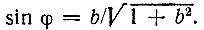На том же рисунке построена кривая Y_А = 1 - е^-α_кt, соответствующая процессу установления амплитуды тока при включении в контур э. д. с. с частотой ω₀, равной резонансной частоте контура.

Из рис. 6.26 видно, что при b ≤ 0,5, т. е. когда Δω/α_к ≤ 0,5, процесс установления частоты практически не отличается от процесса установления амплитуды при внезапном включении э. д. с. Заметное расхождение кривых Y и Y_А наступает при b > 0,5.

Для полноты картины рассмотрим еще изменение амплитуды выходного сигнала. Подставив в выражение (6.87) Δωτ_к = Δω/α_к = b; 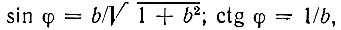получим

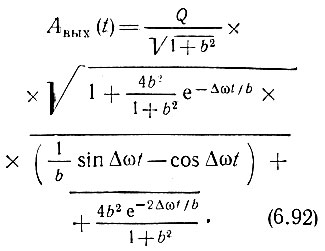
Графики функции для некоторых значений параметра b (рис. 6.27) показывают, что при b ≥ 0,5 изменение частоты сопровождается значительными амплитудными изменениями. При b = 1, т. е. если девиация частоты достигает границ полосы пропускания контура, изменение амплитуды доходит до ∼25% от установившегося значения.

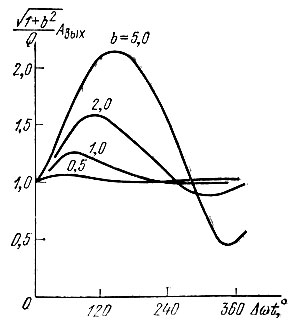
Рис. 6.27. Изменение амплитуды колебания, сопровождающее частотную манипуляцию

Неравенство b = Δω/α_к ≤ 0,5 можно принять в качестве условия монотонного нарастания Δω(t) и отсутствия значительных амплитудных изменений. Длительность же тактового интервала Т₁ (рис. 6.23) должна быть достаточно велика по сравнению с постоянной времени контура τ_к = 1/α_к. Как видим, последнее требование не отличается от требования к τ_к при передаче радиоимпульсов с прямоугольной огибающей.