6.12. Прохождение частотно-модулированного колебания через избирательные цепи

В § 6.9 было показано, что при гармонической модуляции амплитуды передача колебания через контур, точно настроенный на несущую частоту, не сопровождается изменением формы огибающей, имеет место лишь ослабление глубины модуляции.

При частотной модуляции неравномерность амплитудно-частотной и кривизна фазочастотной характеристик оказывают более сложное влияние на параметры выходного колебания. Даже при гармонической модуляции частоты спектр колебания обычно содержит очень большое число пар боковых частот. Нарушение нормальных амплитудных и фазовых соотношений между отдельными парами боковых частот приводит к искажению закона модуляции даже при полной симметрии характеристик цепи относительно несущей частоты колебания.

При ЧМ влияние цепи может сказаться:

- в искажении закона изменения мгновенной частоты и мгновенной фазы колебания;

- в изменении амплитуды полезного частотного отклонения в зависимости от частоты модуляции Ω;

- в возникновении паразитной амплитудной модуляции.

При детектировании колебаний с помощью частотного детектора напряжение на выходе приемника пропорционально изменению мгновенной частоты колебания. Поэтому искажение закона изменения мгновенной частоты в колебательных контурах передатчика и приемника приводит к нелинейным искажениям сигнала, проявляющимся на выходе детектора в виде добавочных напряжений с частотами, кратными основной частоте модуляции Ω.

Второе из отмеченных выше изменений параметров частотно-модулированного колебания приводит к неравномерности частотной характеристики радиолинии с ЧМ и, следовательно, к частотным (линейным) искажениям сигнала.

Рассмотрим воздействие э. д. с., частота которой изменяется по закону

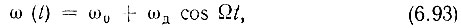
на резонансную колебательную цепь. Амплитуду э. д. с. считаем строго постоянной, так что э. д. с. можно представить выражением [см. (3.23)]

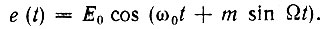
Комплексный коэффициент передачи цепи обозначим через

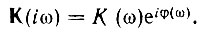
Примерный вид модуля К(ω) и фазы φ(ω) для обычной резонансной цепи изображен на рис. 6.28, а. Так как перед φ(ω) выбран знак плюс, то фазовая характеристика φ(ω) имеет отрицательный наклон в полосе прозрачности цепи^*. Частотный спектр и график изменения мгновенной частоты ω(t) входной э. д. с. показаны на рис. 6.28, б и в. Колебательные цепи обычно настраиваются на среднюю частоту модулированного колебания, поэтому рис. 6.28 и дальнейшее рассмотрение относятся к случаю ω_р = ω₀.

^* (Не зависящий от частоты фазовый сдвиг, например на 90°, как в схеме на рис. 6.27, здесь не учитывается.)

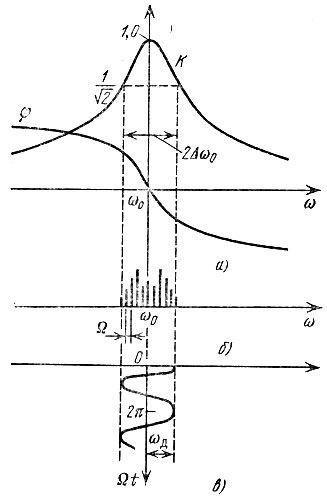
Рис. 6.28. Передаточная функция цепи (а), спектр ЧМ колебания (б) и график мгновенной частоты (в) этого колебания

Для нахождения колебания на выходе цепи в принципе можно воспользоваться тем же методом, что и в случае амплитудной модуляции (см. § 6.9). При этом необходимо учесть изменение амплитуд и фаз для каждой из пар боковых частот э. д. с. в соответствии с кривыми К(ω) и φ(ω). Однако подобный вполне точный метод пригоден лишь при очень малых индексах модуляции, т. е. если состав спектра ЧМ колебания мало отличается от состава спектра АМ колебания. В практике, между тем, чаще всего приходится встречаться с модуляцией, характеризующейся столь большим числом спектральных составляющих в используемой полосе частот, что применение спектрального метода сопряжено с большими, иногда непреодолимыми трудностями вычисления. В таких случаях приходится прибегать к приближенным методам, позволяющим, хотя и не вполне точно, находить колебание на выходе цепи по заданному закону изменения мгновенной частоты э. д. с. и по заданным частотно-фазовым характеристикам цепи без разложения э. д. с. в спектр.

Эти методы, называемые методами мгновенной частоты, основаны на допущении о медленности изменения частоты. Частота модуляции считается настолько малой, что амплитуду и фазу колебания на выходе цепи в каждый момент времени можно без большой погрешности определить по частотной и фазовой характеристикам цепи так же, как и в стационарном режиме. Таким образом, принимается, что установление стационарных колебаний на выходе происходит почти одновременное изменением частоты на входе цепи.

Эти предпосылки тем ближе к истине, чем больше период модуляции 2π/Ω и чем меньше постоянная времени цепи τ. Так как последняя обратно пропорциональна полосе пропускания цепи 2Δω₀, то одним из условий применимости метода мгновенной частоты является неравенство Ω/Δω₀ << 1.

При одной и той же частоте Ω скорость изменения мгновенной частоты э. д. с. зависит от амплитуды частотного отклонения ω_д, поэтому соблюдения только этого неравенства еще недостаточно. Должны быть наложены ограничения и на отношение ω_д/Δω₀. Более подробное рассмотрение [5] показывает, что если ω_д/ω₀ меньше единицы или близко к ней, то метод мгновенной частоты обеспечивает вполне достаточную для практики точность.

При выполнении указанных условий напряжение на выходе цепи можно определить с помощью выражения

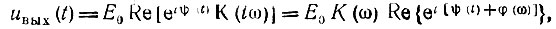
где ψ(t) = ω₀t + m sin Ωt - полная фаза э. д. с. на входе цепи (см. § 3.4); φ(ω) - аргумент коэффициента передачи цепи.

Из этого выражения видно, что амплитуда выходного напряжения изменяется по закону

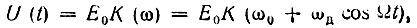
а мгновенная частота - по закону

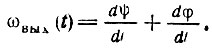
Так как первый член в правой части этого выражения представляет собой мгновенную частоту входной э. д. с. ω(t), то ξ(t) = dφ/dt характеризует влияние рассматриваемой цепи на частоту выходного колебания. При выполнении оговоренного выше условия медленности модуляции величина как правило, мала по сравнению с ω_д. Итак,

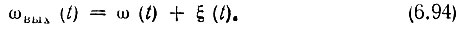
Если известно уравнение фазовой характеристики φ(ω), то, подставляя в (6.94) вместо ω в соответствии с выражением (6.93) величину ω(t) = ω₀ + ω_д cos Ωt и дифференцируя по t, получаем общее выражение для ξ(t):

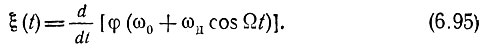
При периодической модуляции частоты ξ(t) также является периодической функцией времени и может быть разложена в ряд Фурье. Так как при настройке цепи на среднее значение вынуждающей частоты ω₀ фазовая характеристика обычно антисимметрична относительно ω₀, то ряд Фурье содержит одни лишь нечетные гармоники: Ω, 3Ω, 5Ω ... Учитывая, наконец, что при изменении частоты по закону (6.93) производная φ, т. е. ξ(t), является нечетной функцией времени, приходим к выводу, что ряд Фурье содержит одни лишь синусоидальные члены, т. е.

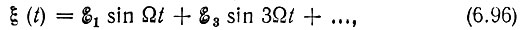
где 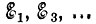- амплитуды гармоник функции ξ(t).

Подставляя выражение (6.96) в (6.94), получаем

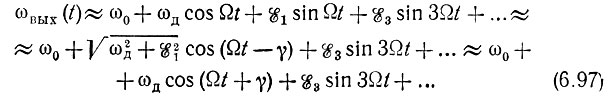
Слагаемое ε²₁ под знаком радикала отброшено как величина высшего порядка малости по сравнению с ω²_д.

Сопоставление выражений (6.93) и (6.97) позволяет сделать вывод, что влияние цепи на выходное колебание заключается в запаздывании фазы сообщения на угол γ, определяемый выражением

и в возникновении нечетных гармоник в законе изменения мгновенной частоты. Как отмечалось выше, наибольшее значение обычно имеет последнее обстоятельство.

Поясним применение метода мгновенной частоты на примере одиночного колебательного контура.

Подразумевая под К(iω) отношение комплексной амплитуды напряжения на конденсаторе к амплитуде э. д. с., включенной последовательно в контур, получаем

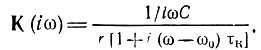
Учитывая, что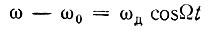

и пренебрегая изменением ω в числителе, так как величина ω_д обычно мала по сравнению с ω₀, можем написать

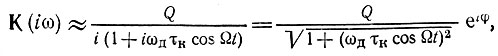
где

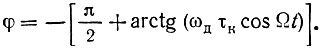
На основании соотношения (6.95) находим

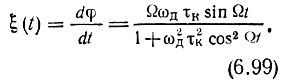
Применяя формулу (2.24), находим

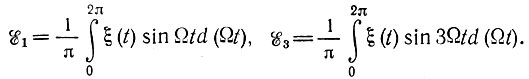
Произведя интегрирование [см. (2.553.3), (2.554.2) и (3.644.3) в [7], получим следующие окончательные формулы для амплитуд первой и третьей гармоник функции ξ(t):

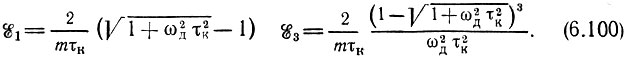
Здесь m = ω_д/Ω.

Далее, по формуле (6.98) находим фазовый сдвиг для сообщения

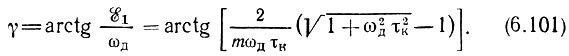
Теперь нетрудно определить коэффициент гармоник по частоте 3Ω на выходе частотного детектора. Для этого нужно разделить амплитуду ε₃ третьей гармоники функции ξ на амплитуду ω_д основной частоты Ω [см. формулу (6.100)]:

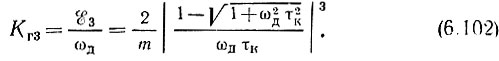
График зависимости mК_г3(ω_дτ_к) изображен на рис. 6.29. При ω_дτ_к << 1 формулы (6.101) и (6.102) упрощаются:

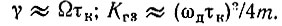
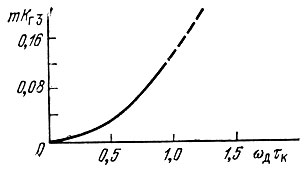
Рис. 6.29. Зависимость коэффициента гармоник от девиации ω_д при заданной величине постоянной времени контура τ_к

При ω_дτ_к → 1 (но m >> 1), т. е. при девиации, почти равной полосе пропускания контура, формулы (6.101) и (6.102) дают

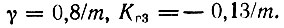
Итак, в условиях, когда метод мгновенной частоты применим, предельные искажения в одиночном контуре не превышают долей процента.

Нетрудно найти амплитудные изменения выходного колебания. Для этого можно воспользоваться резонансной кривой контура и произвести построение, показанное на рис. 6.30. Нетрудно видеть, что основная частота изменения огибающей амплитуд U вдвое превышает частоту модуляции Ω.

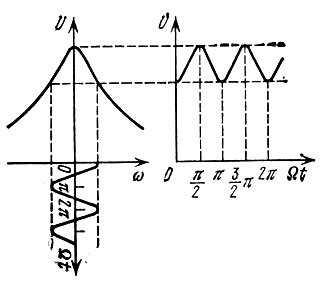
Рис. 6.30. Возникновение паразитной амплитудной модуляции при модуляции частоты