Глава 7. Прохождение случайных колебаний через линейные цепи с постоянными параметрами

7.1. Преобразование характеристик случайного процесса

Ограничиваясь рассмотрением стационарных случайных процессов, поставим задачу следующим образом: на входе линейного четырехполюсника (рис. 7.1) с передаточной функцией К(iω) и импульсной характеристикой g(t) действует напряжение s(t), представляющее собой случайную функцию времени с энергетическим спектром W_s(ω) и корреляционной функцией В_s(τ); требуется найти энергетический спектр W_{s вых}(ω) и корреляционную функцию B_{s вых}(τ) колебания s_вых(t) на выходе четырехполюсника.

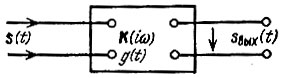
Рис. 7.1. Линейный четырехполюсник с постоянными параметрами

Задача легко решается с помощью рассуждений, приводящих к определению понятия "энергетический спектр случайного процесса" [в § 4.3 см. (4.31)-(4.33)].

Если спектральную плотность |Х_kT(ω)| k-й реализации в формуле (4.32) умножить на модуль передаточной функции К(ω), получим спектральную плотность этой же реализации на выходе четырехполюсника. Отсюда вытекает следующее соотношение:

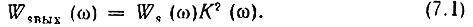
Возведение передаточной функции в квадрат объясняется тем, что W_s(ω) является спектральной плотностью мощности случайной функции, между тем как К(ω) определяет отношение напряжений (или токов) на выходе и входе.

То обстоятельство, что фазочастотная характеристика фильтра не играет никакой роли при определении W_{s вых}(ω), объясняется случайностью фаз спектральных составляющих входного колебания; добавление к ним фазовых сдвигов в фильтре ничего не изменяет в структуре колебания.

Корреляционная функция случайного процесса на выходе фильтра определяется с помощью выражения (4.39):

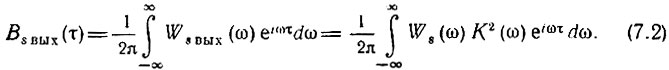
Соотношения между статистическими характеристиками случайных процессов на входе и выходе цепи можно вывести также и на основе заданной импульсной характеристики цепи.

Действительно, поскольку спектральной функции W_s(ω) соответствует корреляционная функция

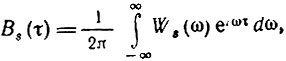
а спектральной функции К²(ω) -

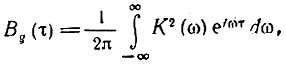
т. е. корреляционная функция импульсной характеристики g(t) [см., например, (2.118), в которой нужно S²(ω) заменить на К²(ω)], то произведению спектральных функций W_s(ω) и К²(ω) соответствует свертка функций В_s(τ) и В_g(τ) [см. (2.64)]:

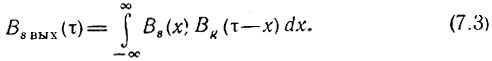
Таким образом, по заданным корреляционным функциям В_s(τ) и В_g(τ) определяется корреляционная функция на выходе В_{s вых}(τ), после чего находится энергетический спектр

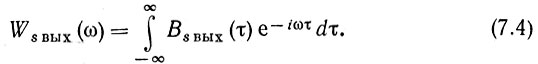
Итак, спектральный и корреляционный анализ прохождения стационарного случайного процесса через линейную цепь с постоянными параметрами не связан с какими-либо трудностями.

Иначе обстоит дело с определением закона распределения случайного процесса на выходе линейной цепи. В общем случае при произвольном распределении процесса на входе отыскание распределения на выходе инерционной цепи представляет собой весьма сложную задачу.

Трудности отпадают при нормальном распределении входного процесса, так как при любых линейных операциях с нормальным процессом (усиление, фильтрация, дифференцирование, интегрирование и т. д.) распределение остается нормальным, изменяются лишь функции В(τ) и W(ω). Поэтому, если задана плотность вероятности входного процесса (с нулевым средним)

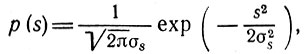
то плотность вероятности на выходе линейной цепи

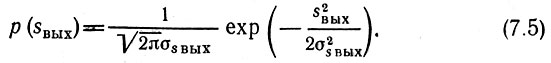
В соответствии с (4.36) дисперсия выходного процесса определяется выражением

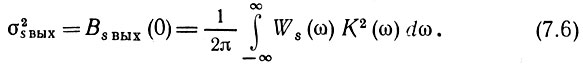
Анализ передачи нормальных процессов через линейные цепи по существу сводился к корреляционному (или спектральному) анализу.