7.2. Характеристики собственных шумов в радиоэлектронных цепях

При анализе передачи сигналов по радиотехническим цепям наряду с неизбежными искажениями формы сигналов необходимо учитывать также и собственные шумы цепи. Эти шумы, накладываясь на сигнал, ограничивают информационную емкость последнего. Проблема шумов особенно актуальна при усилении слабых сигналов.

В радиоэлектронных устройствах имеются два основных источника шумов: дискретная структура тока в усилительных элементах (транзисторы, электронные лампы и т. д.) и тепловое движение свободных электронов в проводниках электрической цепи.

Рассмотрим первый источник на примере дробового эффекта, присущего электронному току в усилительных приборах. Этот ток представляет собой совокупность импульсов, каждый из которых обусловлен переносом заряда одного электрона. Полный ток, являющийся суммой очень большого числа перекрывающихся, расположенных случайным образом на оси времени импульсов, представляет собой стационарный эргодический случайный процесс, для которого справедлива центральная предельная теорема^*. Поэтому распределение электронного тока можно считать нормальным с плотностью вероятности

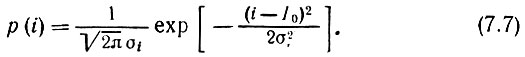
^* (Содержание этой теоремы сводится к следующему: распределение суммы достаточно большого числа случайных, взаимно независимых слагаемых, среди которых нет доминирующих, близко к нормальному независимо от законов распределения отдельных слагаемых.)

Постоянную составляющую тока I₀ и среднюю мощность флуктуационной составляющей σ²_i можно определить с помощью следующих рассуждений.

Пусть среднее за 1 с число импульсов тока равно k₁. Так как каждый импульс переносит заряд одного электрона е, то полное количество электричества, переносимое в среднем за 1 с, равно k₁e. Это и есть постоянная составляющая тока. Таким образом,

Введем в рассмотрение спектральную плотность G₁(ω) одиночного импульса тока i_e(t - t_k), обусловленного переносом заряда е одного электрона (t_k - момент вылета электрона). Независимо от формы этого импульса значение G₁(ω) при ω = 0 равно площади импульса (см. § 2.9, п. 1):

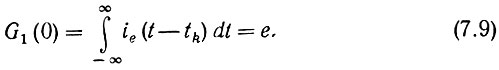
Длительность τ_e импульса i_e(t) зависит от геометрии электронного прибора, от напряженности электрического поля в междуэлектродных промежутках и т. д. Ширину спектра импульса в грубом приближении можно приравнять 2/те. Таким образом, модуль спектральной плотности импульса i_e(t - t_k) можно представить в виде графика, показанного на рис. 7.2. Максимальная ордината ∼e.

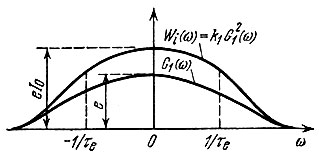
Рис. 7.2. Спектральная плотность G₁(ω) одиночного импульса и энергетический спектр W_i(ω) случайного процесса

Энергия одного импульса по формуле Парсеваля равна

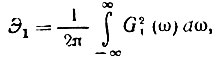
а суммарная энергия k₁ импульсов за 1 с, т. е. средняя мощность процесса (при сопротивлении 1 Ом).

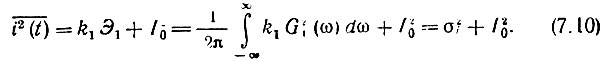
Первое слагаемое в правой части (7.10) учитывает мощность флуктуационной составляющей тока Увеличение этой мощности всего лишь в k₁ раз (а не в k²₁ раз) объясняется случайностью фаз гармонических составляющих от отдельных импульсов, хаотически расположенных на оси времени. Иными словами, спектральные составляющие различных импульсов на всех частотах, кроме ω = 0, некогерентны (см. § 2.18) и складываются по мощности аддитивно. Второе слагаемое в (7.10) учитывает мощность постоянной составляющей I₀.

Из первого слагаемого в правой части выражения (7.10) вытекает, что энергетический спектр флуктуационной составляющей электронного тока совпадает по форме со спектральной плотностью энергии G²₁(ω) отдельных импульсов, образующих случайный процесс

Примерный вид W_i(ω) представлен на рис. 7.2.

Учитывая, что k₁ = I₀/е, а также то, что в пределах полосы частот ∼2/τ_е имеет место равенство (7.9), получаем^*

^* (В технической литературе также распространения формула W_i(ω) = 2 eI₀, при выводе которой среднюю мощность σ²_i относят только к положительным частотам.)

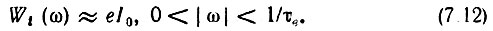
Выражения (7.7) и (7.12) определяют основные статистические характеристики дробового тока.

Теперь нетрудно выявить статистические характеристики напряжения шума на выходе цепи, содержащей "шумящий" элемент. На рис. 7.3, а и б изображены схемы транзисторного и лампового усилителей, а на рис. 7.3, в - единая схема замещения для флуктуационного тока i(t). Входные зажимы база - эмиттер (соответственно сетка - катод) соединены накоротко, чтобы подчеркнуть отсутствие внешнего воздействия на усилитель. В качестве источника шума на схеме замещения показан генератор тока i(t), статистические характеристики которого р(i) и W_i(ω) были определены выше.

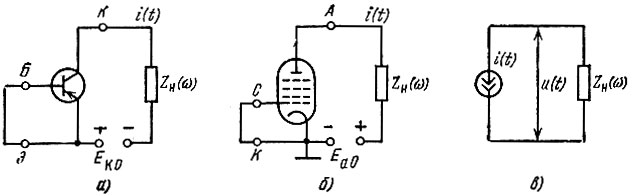
Рис. 7.3. Транзисторный (а) и ламповый (б) усилителя и единая схема замещения для флуктуационного тока (в)

Напряжение шума u(t), создаваемое на линейном нагрузочном элементе Z_н(ω), распределено, как и ток i(t), по нормальному закону

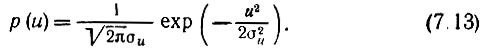
Энергетический спектр напряжения u(t) определяется соотношением

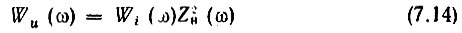
[сравнить с (7.1); в данном случае вместо безразмерной передаточной функции К(ω) фигурирует сопротивление Z_н(ω)].

Применяя к (7.14) преобразование (4.39), можно определить корреляционную функцию напряжения шума на выходе усилителя, а также величину σ_u, т. е. среднеквадратическое напряжение шума.

Рассмотрим механизм формирования собственного шума в резистивном и резонансном усилителях.

В резистивном усилителе сопротивление Z_н(iω) определим для схемы на рис. 5.14, б по формулам

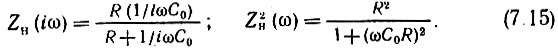
Постоянная времени цепи R, С₀ во много раз больше, чем длительность импульса τ_в; соответственно полоса пропускания цепи R, C₀, примыкающая к нулевой частоте, во много раз уже, чем ширина энергетического спектра W_i(ω), показанного на рис. 7.2. Поэтому при определении воздействия на цепь дробового шума его можно рассматривать как белый шум с энергетическим спектром W_i(ω) = еI₀. Тогда по формуле (7.14)

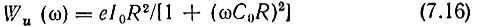
и по формуле (4.39)

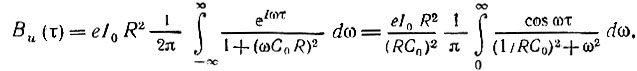
Входящий в правую часть интеграл равен

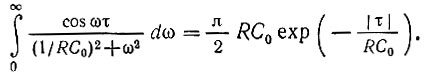
Таким образом,

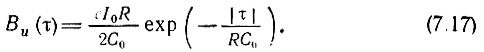
При τ = 0 это выражение определяет дисперсию напряжения шума σ²_u, и среднеквадратическое напряжение σ_u:

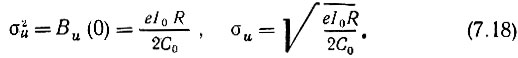
Нормированная корреляционная функция шума принимает вид

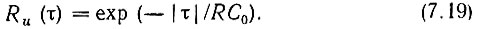
Графики энергетического спектра W_u(ω) и функции R_u(τ) изображены на рис. 7.4 и 7.5.

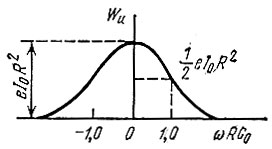
Рис. 7.4. Энергетический спектр шумового напряжения на выходе резистивного усилителя

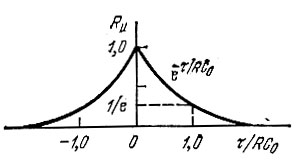
Рис. 7.5. Нормированная корреляционная функция шума, соответствующая спектру W_u(ω) (рис. 7.4)

Интервал корреляции напряжения шума в данном примере определяется величиной |τ|/RC₀ ≈ 1. Нетрудно пояснить смысл полученного результата. Напряжение шума на нагрузке образуется совокупностью беспорядочно следующих импульсов тока, создаваемых отдельными электронами. Каждый из этих импульсов создает импульс напряжения, длительность которого определяется постоянной времени нагрузки. При наложении большого числа импульсов относительная скорость изменения суммарного напряжения шума u(t) должна быть того же порядка, что и скорость изменения отдельных импульсов. Поэтому для независимости напряжений, отсчитываемых в моменты t и t + τ, величина τ должна быть не менее длительности импульсов, образующих шум.

Для количественной оценки уровня напряжения шума, создаваемого дробовым эффектом, приведем следующий пример, характерный для апериодического усилителя: постоянный ток I₀ = 10 мА, сопротивление нагрузки 5 кОм, емкость С₀ = 50 пФ.

Применяя формулу (7.18), находим среднеквадратическое напряжение шума на выходе усилителя

Определенное таким образом напряжение можно условно рассматривать как результат приложения некоторого напряжения шума ко входу усилителя. При коэффициенте усиления К_у эквивалентное напряжение шума на входе следует приравнять величине u_ск = σ_u/К_у. При коэффициенте усиления К_у ≈ 100 получаем σ_u ≈ 3 мкВ. Эта величина и определяет нижний порог сигнала, который еще имеет смысл усиливать данным усилителем.

Аналогичным образом можно рассмотреть формирование шума в колебательной цепи резонансного усилителя, схема которого изображена на рис. 5.17.

По аналогии с выражением (7.16) определим энергетический спектр

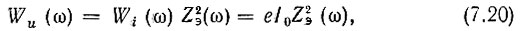
где

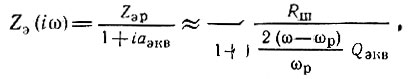
а Z_эр = R_ш - сопротивление контура (шунтированного резистором R_ш) при резонансе. Отсюда квадрат модуля сопротивления нагрузки

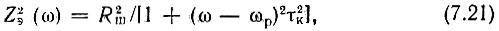
где τ_к = 2Q_экв/ω_p - постоянная времени контура.

Таким образом,

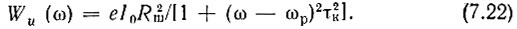
График энергетического спектра W_u(ω) изображен на рис.7.6.

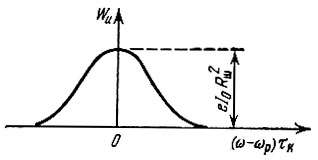
Рис. 7.6. Энергетический спектр шумового напряжения на выходе резонансного усилителя

Выражение (4.39) для функции корреляции в данном случае принимает следующий вид:

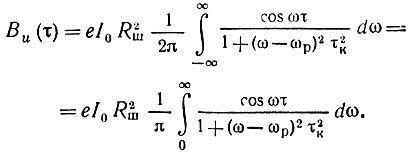
Переходя к новой переменной ω₁ = ω - ω_р, получаем

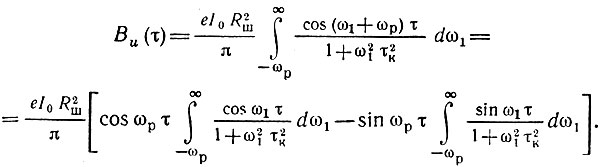
Заметим, что при достаточно большой добротности контура выполняется условие

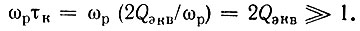
Поэтому нижний предел интегралов -ω_р можно заменить на -∞. Второй интеграл обращается при этом в нуль ввиду нечетности подынтегральной функции относительно переменной интегрирования ω₁. Первый же интеграл ввиду четности подынтегральной функции приводится к виду

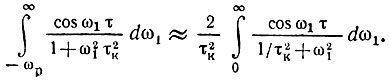
Аналогичный интеграл был вычислен при выводе формулы (7.17). Используя этот результат, получаем

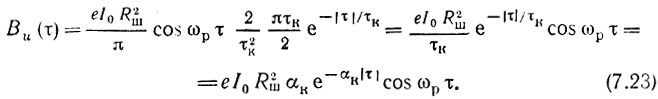
Здесь через α_к = 1/τ_к обозначено затухание контура. Учитывая, что при шунтировании контура сопротивлением R_ш коэффициент затухания равен α_к = 1/2R_шС, записываем формулу (7.23) в следующей форме:

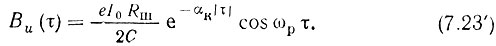
Из формул (7.23), (7.23') вытекает, во-первых, что средний квадрат напряжения шума на контуре равен

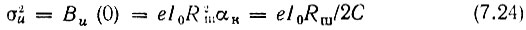
и, следовательно, среднеквадратическое напряжение шума 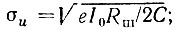во-вторых, нормированная корреляционная функция определяется выражением

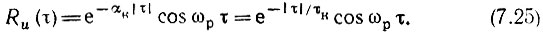
График функции R_u(τ) показан на рис. 7.7. Интервал корреляции в рассматриваемом случае определяется ходом огибающей функции R_u(τ), т. е. множителем е^-|τ|/τ_к в выражении (7.25).

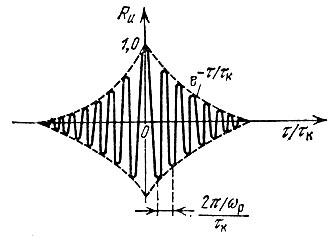
Рис. 7.7. Нормированная корреляционная функция, соответствующая спектру W_u(ω) (рис. 7.6)

Пересчет напряжения шумов ко входу усилителя, как и для апериодического усилителя, можно сделать по формуле u_ск = σ_u/К_у, в которой под К_у следует подразумевать коэффициент усиления на резонансной частоте.

Структура напряжения шума, выделяемого на высокодобротном колебательном контуре, имеет вид, показанный на рис. 4.17. Приведенные в § 4.6 характеристики узкополосного случайного процесса могут быть полностью отнесены к дробовому шуму в резонансном усилителе.

Нужно иметь в виду, что изложенный в данном параграфе материал дает представление лишь о методе анализа характеристик собственных шумов, формируемых избирательной цепью усилителя. Механизм образования шумов зависит от ряда физических и конструктивных особенностей усилительных (активных) элементов, которые здесь не рассматриваются.

В заключение укажем, что приведенные выше соотношения можно использовать также при анализе формирования в избирательных цепях теплового шума. Необходимо лишь энергетический спектр такого шума определять по формуле, известной из физики,

где R - сопротивление резистора, генерирующего шум; k = 1,38⋅10^-23 Вт⋅с/град - постоянная Больцмана; Т - абсолютная температура.

Как и в выражении (7.12), W_u(ω) здесь определено для положительных и отрицательных частот. При отнесении мощности шума только к положительным частотам коэффициент 2 следует заменить на 4.