7.3. Дифференцирование случайной функции

Пусть задан стационарный эргодический случайный процесс s(t) с энергетическим спектром W_s(ω) и корреляционной функцией B_s(τ) и требуется найти аналогичные характеристики для производной s(t). Не останавливаясь здесь на рассмотрении всех условий дифференцируемости случайной функции, ограничимся основным требованием: энергетический спектр W_s(ω) при ω → ∞ должен убывать быстрее, чем 1/ω², так что

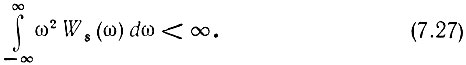
Это условие выполняется для большинства практических задач, так как энергетический спектр W_s(ω) формируется физической цепью, передаточная функция которой при ω → ∞ убывает быстрее, чем 1/ω (а ее квадрат модуля уменьшается быстрее, чем 1/ω²). Условию (7.27) не отвечает белый шум с бесконечно широким спектром, однако обычно рассматривается шум с ограниченным спектром.

Считая условие (7.27) выполненным, рассмотрим прохождение случайного сигнала s(t) через идеальную дифференцирующую цепь, передаточная функция которой К(iω) = iωτ₀ [см. (6.17)].

Применяя выражения (7.1), (7.2), можем написать

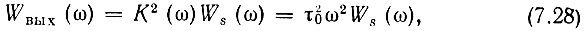
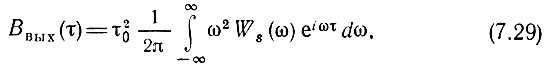
Дисперсия процесса на выходе устройства

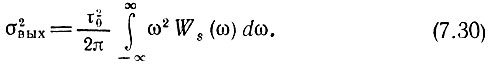
Рассмотрим следующий пример: пусть спектр процесса на входе дифференцирующего устройства равномерен в полосе частот -f₁ ≤ f ≤ f₁:

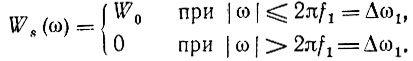
Корреляционная функция подобного процесса [см. (4.41)]

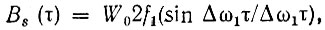
а дисперсия

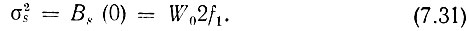
Нормированная корреляционная функция

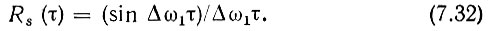
После дифференцирования соответственно получаем

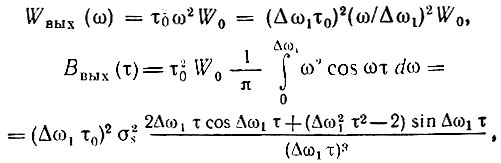
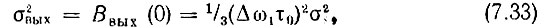
где у(τ) - дробь в выражении для В_вых(τ).

Графики функций W_s(ω) и W_вых(ω), а также функций R_s(τ) и R_вых(ω) изображены на рис. 7.8, а и б; параметр Δω₁τ₀ приравнен единице. Из этих графиков видно, что дифференцирование приводит к ослаблению нижних частот исходного процесса. Относительное возрастание высших частот приводит к более четко выраженной осцилляции корреляционной функции (рис. 7.8, б).

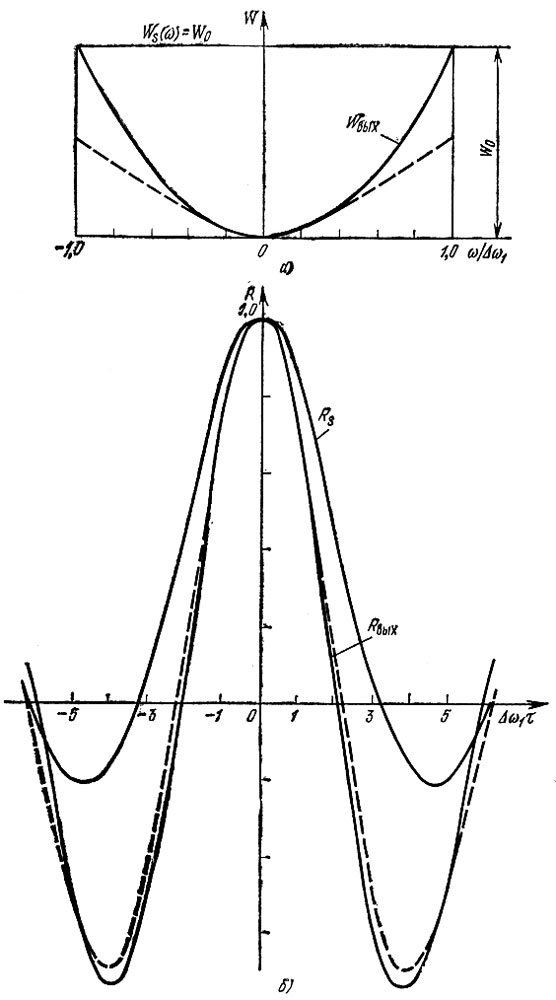
Рис. 7.8. Энергетические спектры (а) и корреляционные функции (б) на входе и выходе дифференцирующей цепи: ^____ на выходе идеальной цепи; --- на выходе RC-цепи

Рассмотрим теперь прохождение того же случайного сигнала через реальное дифференцирующее устройство в виде RС-цепи (рис. 6.5, б). Квадрат передаточной функции дифференцирующей цепи в соответствии с (6.19)

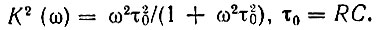
Таким образом, энергетический спектр на выходе цепи

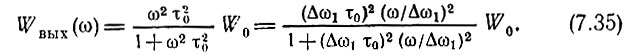
График W_вых(ω) для Δω₁τ₀ = 1 представлен на рис. 7.8, а штриховой линией.

Корреляционная функция

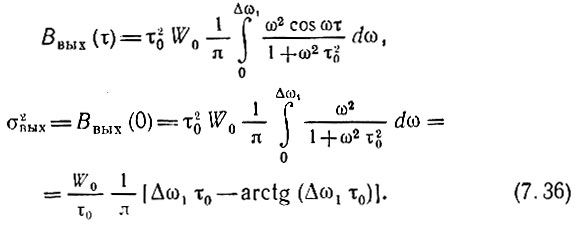
Результат вычисления нормированной корреляционной функции R_вых(τ) = B_вых(τ)/σ²_вых представлен на рис. 7.8, б штриховой линией (для Δω₁τ₀ = 1).

Можно считать, что при Δω₁τ₀ ≤ 1 физическая RC-цепь осуществляет дифференцирование рассматриваемого случайного процесса, близкое к точному дифференцированию.