7.4. Интегрирование случайной функции

Для выявления некоторых особенностей интегрирования случайной функции рассмотрим сначала прохождение стационарного случайного процесса через физическую интегрирующую RС-цепь (рис. 6.6, б).

Пусть на входе этой цепи начиная с момента t = -∞ действует случайная функция s(t) с энергетическим спектром W_s(ω) и корреляционной функцией В_s(ω). Считая процесс на выходе установившимся, мы можем определить W_вых(ω) и B_вых(τ) с помощью выражений (7.1) и (7.2), подставив в них [см. (6.20)]

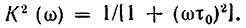
Таким образом,

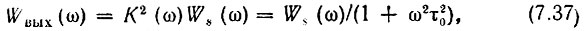
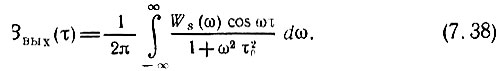
Рассмотрим два частных случая: 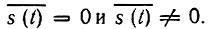В первом случае энергетический спектр W_s(ω) не содержит слагаемого с δ-функцией [см. (4.35)-(4.37)], полагая W_s(ω) = W₀ = const (белый шум), получаем корреляционную функцию

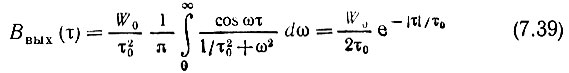
и дисперсию

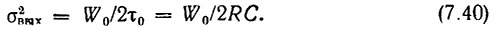
во втором случае (при 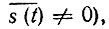когда в соответствии с (4.35) энергетический спектр

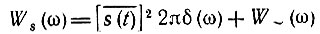
причем 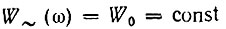(как и в предыдущем случае), корреляционная функция и дисперсия будут

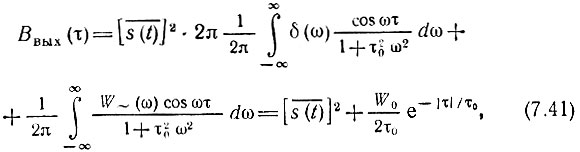
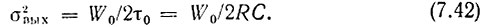
Из приведенных соотношений видно, что в установившемся режиме процесс на выходе физической интегрирующей цепи является стационарным, как и на входе.

Иначе обстоит дело при точном математическом интегрировании, которому соответствует нереализуемая передаточная функция

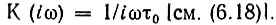
Условие интегрируемости случайного процесса при этом принимает следующий вид:

Если условие дифференцируемости случайной функции (7.27) накладывало требование достаточно быстрого убывания W_s(ω) при ω → ∞, то при интегрировании аналогичное требование относится к поведению W_s(ω) при ω → 0.

Интегрирование стационарного процесса s(t) с W_s(0) ≠ 0 приводит к нестационарному процессу с неограниченно возрастающей дисперсией.

Если 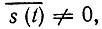то математическое ожидание процесса на выходе также неограниченно возрастает.

Следует иметь в виду, что идеальное интегрирующее устройство можно рассматривать как фильтр с бесконечно малой полосой пропускания. Процесс установления в таком фильтре длится бесконечно долго. Поэтому статистические характеристики интеграла случайного процесса существенно зависят от пределов интеграла, т. е. от длительности интегрирования.