7.5. Нормализация случайных процессов в узкополосных линейных цепях

Пусть на входе линейной цепи (с постоянными параметрами) действует стационарный случайный процесс с распределением, отличным от нормального. Если интервал корреляции этого процесса меньше постоянной времени цепи (т. е. ширина энергетического спектра больше полосы пропускания цепи), то распределение случайного процесса на выходе приближается к нормальному. Эффект нормализации проявляется тем сильнее, чем уже полоса пропускания цепи. Поясним это положение на двух примерах.

Сначала рассмотрим воздействие на высокодобротный колебательный контур последовательности коротких, неперекрывающихся, случайным образом расположенных на оси времени импульсов (рис. 7.9), причем постоянная времени контура τ_к велика по сравнению со средней величиной интервалов между импульсами. Напряжение на контуре в какой-либо момент времени t₁ является суммой свободных колебаний, вызванных предыдущими импульсами и не успевших полностью затухнуть к рассматриваемому моменту. Чем уже полоса пропускания цепи, тем длительнее свободные колебания и, следовательно, тем большее число соизмеримых по величине и некоррелированных слагаемых принимает участие в образовании результирующего напряжения в момент t₁. В соответствии с центральной предельной теоремой эти предпосылки достаточны для приближения распределения к нормальному закону.

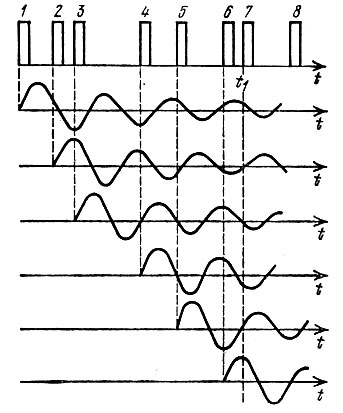
Рис. 7.9. Отклики колебательной цепи на отдельные импульсы хаотической последовательности

При спектральном подходе эффект нормализации можно объяснить следующим образом. Спектр колебания в контуре суммируется из спектров отдельных импульсов входной последовательности. Внутри каждого из этих парциальных спектров фазы спектральных составляющих полностью коррелированы, а между фазами составляющих из различных спектров никакой корреляции нет (из-за случайной расстановки импульсов на оси времени). Чем уже полоса прозрачности контура, тем меньшую роль играет корреляция фаз в парциальных спектрах.

Приведем теперь другой пример, поясняющий явление нормализации в узкополосной цепи. Пусть на контур воздействует непрерывное колебание с постоянной амплитудой и с частотой, модулированной по пилообразному закону со случайным периодом (рис. 7.10). При каждом пробеге частоты через полосу прозрачности контура 2Δω₀ в последнем возникает свободное колебание, амплитуда которого обратно пропорциональна наклону "пилы". Так как моменты пересечения полосы прозрачности расположены на оси времени случайным образом, то и свободные колебания образуют импульсную последовательность со случайными интервалами (t_k, t_{k + 1}).

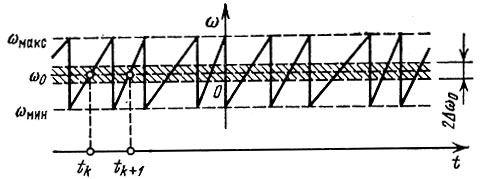
Рис. 7.10. Изменение частоты колебания по пилообразному закону со случайным периодом

При медленном качании частоты, когда интервалы велики по сравнению с постоянной времени контура τ_к, свободные колебания не перекрываются. Предположим, что τ_к велико по сравнению со средним значением интервалов Т_ср. Тогда в любой момент времени будет накладываться много колебаний со случайными и взаимно независимыми фазами и амплитудами. При этом входное колебание, закон распределения которого определяется формулой (4.25) (изменение мгновенной частоты не отражается на одномерном законе распределения высокочастотного колебания с постоянной амплитудой), преобразуется в случайную функцию с распределением, близким к нормальному. Нормализация будет тем полнее, чем больше τ_к по сравнению с T_ср.

Учитывая, что для одиночного контура имеет место соотношение Δω₀τ_к = 1, а средняя частота "пилы" F_cp = 1/Т_ср, условие нормализации можно записать в форме неравенства

В широкополосных линейных цепях при некоторых условиях может иметь место эффект, обратный описанному выше эффекту нормализации: распределение процесса на выходе цепи может отличаться от нормального распределения больше, чем на входе. Можно привести простой пример подобного эффекта.

Пусть на вход дифференцирующего устройства подается совокупность относительно длинных импульсов, имеющая распределение, близкое к нормальному. В результате дифференцирования каждый из импульсов превращается на выходе в пару очень коротких импульсов, соответствующих фронтам входного импульса. Число взаимно перекрывающихся импульсов на выходе сокращается, благодаря чему приближение к нормальному закону на выходе оказывается худшим, чем на входе. Подобный эффект иногда называют "денормализацией" процесса.

Следует подчеркнуть, что отмеченный эффект не противоречит тому, что в любой линейной цепи нормальный процесс сохраняет нормальный закон распределения. Если в приведенном выше примере среднее число импульсов в единицу времени довести до бесконечности (что необходимо для получения строго нормального распределения), то при любом сжатии импульсов, которое можно осуществить в физически реализуемой цепи, процесс будет нормальным также и на выходе цепи.