7.6. Распределение суммы гармонических колебаний со случайными фазами

Этот вопрос приобретает большое значение в связи с распространенностью спектрального представления сигналов и случайных процессов. Из центральной предельной теоремы (см. сноску ранее) вытекает, что суммирование достаточно большого числа гармонических колебаний со случайными и взаимно независимыми амплитудами и фазами образует случайную функцию с нормальным законом распределения

В практике часто встречаются задачи, в которых число слагаемых относительно мало, так что условия применимости центральной предельной теоремы на выполняются и полной нормализации не наблюдается.

Для выяснения зависимости степени нормализации от числа случайных слагаемых (с не нормальным распределением) можно воспользоваться методом характеристических функций.

В теории вероятностей под характеристической функцией θ(η) случайной величины х, или характеристической функцией данного распределения р(х), подразумевается среднее значение функции e^iηх, т. е.

Здесь η - вещественная переменная.

При заданной плотности вероятности р(х) среднее значение величины e^iηх можно определить с помощью выражения

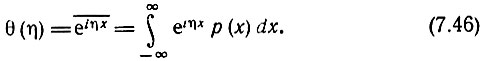
Правая часть этого выражения есть не что иное, как преобразование Фурье функции р(х). Следовательно, если известна характеристическая функция θ(η) какой-либо случайной величины х, то плотность вероятности р(x) можно найти с помощью обратного по отношению к (7.46) преобразования Фурье

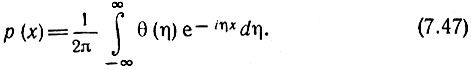
Характеристическая функция обладает рядом важных свойств, позволяющих весьма просто определять параметры распределения р(х). Для поставленной выше задачи особенно важно, что для N взаимно независимых слагаемых х₁, х₂, ..., x_N характеристическая функция суммы имеет следующий вид:

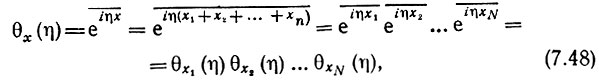
т. е. характеристическая функция суммы независимых случайных величин равна произведению характеристических функций слагаемых.

Для частного случая, когда все слагаемые обладают одинаковыми распределениями и, следовательно, одинаковыми характеристическими функциями, получаем

Для наиболее важного и распространенного в природе нормального закона распределения

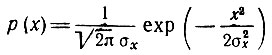
характеристическая функция в соответствии с (7.46) равна

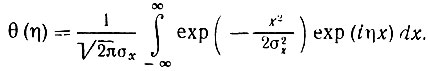
С помощью преобразований, аналогичных (2.75) и (2.77), получаем^*

^* (В общем случае, когда среднее значение случайной величины не равно нулю и

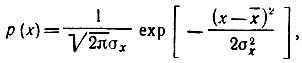
характеристическая функция

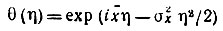
(см., например, [7]).)

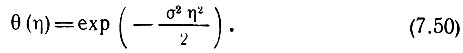
Таким образом, при нормальном распределении график характеристической функции относительно η имеет такую же форму, как и график плотности вероятности относительно х. Поэтому о степени приближения распределения какой-либо случайной величины к нормальному закону можно судить по тому, насколько характеристическая функция рассматриваемой величины приближается к функции, определяемой выражением (7.50).

Используем выражения (7.46)-(7.50) в задаче о распределении суммы нескольких синусоидальных колебаний со случайными фазами.

Для выборки х, взятой из гармонического колебания с амплитудой А₀ и со случайной фазой, плотность вероятности [см. (4.25)]

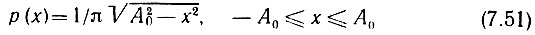
С помощью выражения (7.46) находим характеристическую функцию этого распределения

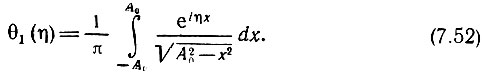
Подставляя 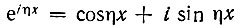и учитывая, что sin ηx/√(А₀²-x²) является нечетной функцией х, получаем (см. 3.753.2 в [7])

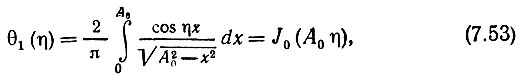
где J₀ - бесселева функция первого рода нулевого порядка.

Для выборки, взятой из суммы N гармонических колебаний с одинаковыми амплитудами A₀/N, но со случайными взаимно независимыми фазами, характеристическая функция в соответствии с (7.49) будет

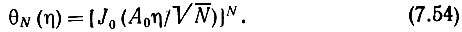
Амплитуда каждой из синусоид приравнена 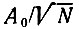для того, чтобы дисперсия суммы, равная 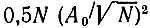оставалась при увеличении числа синусоид неизменной.

На рис. 7.11 изображены характеристические функции для различных значений N. При N ≥ 4...5 функция θ_η(η) быстро приближается к предельной кривой N → ∞, соответствующей нормальному распределению суммы.

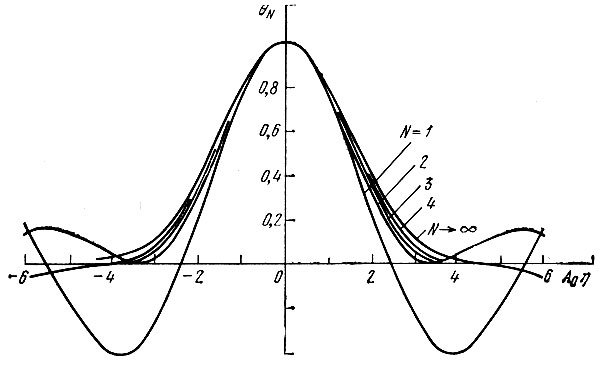
Рис. 7.11. Характеристические функции для суммы N гармонических колебаний со случайными фазами

Для отыскания плотности вероятности суммы N гармонических колебаний необходимо в соответствии с выражением (7.47) вычислить интеграл

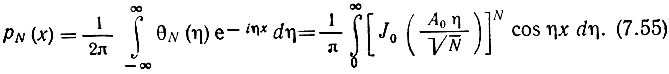
При N = 1 получается исходное выражение р(х) для одной синусоиды [формула (7.51)], а при N = 3...4 функции p_N(x) имеют вид, показанный на рис. 7.12, построенном для А₀ = 1 (интегралы были вычислены с помощью приближенного метода). Сплошной линией изображена функция p_N(x) при нормальном распределении (N → ∞).

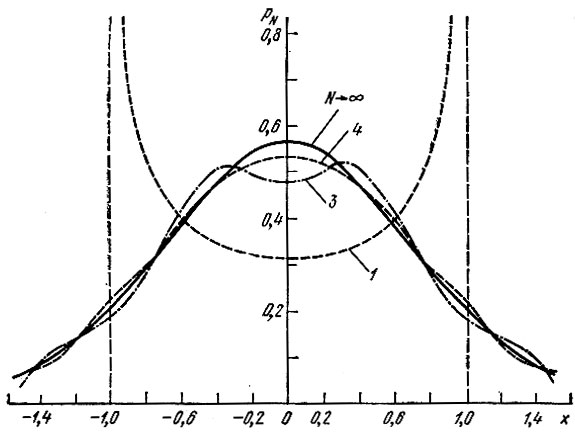
Рис. 7.12. Плотность вероятности суммы N гармонических колебаний со случайными фазами (рис. 7.11)

Полученные результаты показывают, что при суммировании хотя бы пяти-шести гармонических колебаний со случайными и взаимно независимыми фазами получается стационарный случайный процесс, близкий к нормальному.

Это справедливо для значений х, заключенных в области 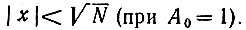При больших значениях |х| р_N(х) = 0, в то время как при нормальном распределении р(х) отлично от нуля. Таким образом, при конечном числе слагаемых N на "хвостах" кривой распределения неизбежно расхождение между р_N(х) и р_∞(х).

Отмеченная выше стационарность суммы вытекает из стационарности исходного процесса (совокупности гармонических колебаний со случайными фазами). Далее, поскольку плотность вероятности р(х), определяемая формулой (7.51), не зависит от частоты, то и р_N(х) не зависит от частоты.

Следует, однако, иметь в виду, что при суммировании гармонических колебаний с одинаковыми частотами получается процесс хотя и стационарный, но не эргодический. Каждая из реализаций суммарного процесса представляет собой в этом случае гармоническое колебание, отличающееся от других реализаций лишь амплитудой и фазой (в зависимости от того, с какими фазами сложились N исходных колебаний в данной реализации). При усреднении х² "вдоль процесса" для каждой k-й реализации получается свое значение 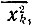не совпадающее с истинной дисперсией σ_x², определяемой при усреднении по множеству ("поперек процесса").

При суммировании гармонических колебаний не только со случайными начальными фазами, но и с различными частотами получается процесс не только стационарный, но и эргодический (при достаточно больших значениях N).

Итак, суммирование достаточно большого числа некоррелированных гармонических колебаний приводит к стационарному процессу, близкому к нормальному.