Глава 8. Нелинейные цепи и методы их анализа

8.1. Нелинейные элементы

Основные радиотехнические преобразования осуществляются с помощью либо нелинейных цепей, либо линейных цепей с переменными параметрами. Однако последние реализуются тоже с помощью нелинейных элементов (например, емкость р-n-перехода в полупроводниковом диоде), а некоторые параметрические цепи сами работают в существенно нелинейном режиме (например, параметрический генератор). Поэтому можно считать, что свойства нелинейных элементов и цепей являются фундаментом для теории большинства реальных радиотехнических устройств. Приведем некоторые примеры нелинейных элементов.

Следует различать резистивные (сопротивления) и реактивные (индуктивности, емкости) нелинейные элементы.

Для радиотехнических цепей и устройств наиболее характерными и распространенными резистивными нелинейными элементами являются полупроводниковые, ламповые и любые другие приборы, используемые для усиления или преобразования сигналов и имеющие нелинейную вольт-амперную характеристику. Важным параметром резистивного нелинейного элемента является определенная соответствующим образом крутизна его характеристики.

Различают два следующих определения крутизны характеристики: а) в рассматриваемой рабочей точке при слабом сигнале (дифференциальная крутизна) и б) крутизна при сильном гармоническом колебании (средняя крутизна).

С первым определением крутизны, соответствующим линейному режиму работы прибора (рис. 8.1, а), мы имели дело в гл. 5, 6, где эта крутизна определялась выражением [см. (5.37'), (5.40)] вида

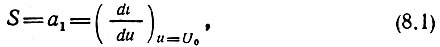
где U₀ приравнивалось U_{БЭ 0} (для транзистора).

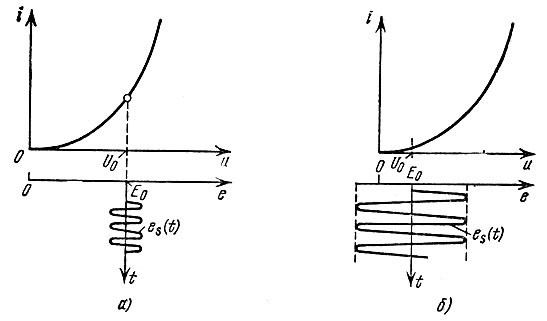
Рис. 8.1. Линейный (а) и нелинейный (б) режимы работы элемента с нелинейной вольт-амперной характеристикой

Второе определение крутизны соответствует существенно нелинейному режиму работы устройства (рис. 8.1, б) и может быть дано лишь при учете формы вольт-амперной характеристики нелинейного элемента в пределах изменения входного воздействия (это будет сделано в § 8.4).

Примером нелинейной емкости может служить любое устройство, обладающее нелинейной вольт-кулонной характеристикой q(u). На рис. 8.2 изображены вольт-кулонная характеристика q_л(u) и вольт-фарадная характеристика С_л = q_л(u)/u = const для обычной линейной емкости и аналогичные характеристики q_нл и С_нл = q_нл(u)/u для нелинейной.

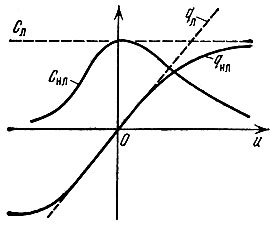
Рис. 8.2. Вольт-кулоная и вольт-фарадная характеристики линейного и нелинейного конденсатора

При любом характере зависимости C_нл для заряда q_нл, как и в случае линейной емкости, имеет место соотношение

В дальнейшем нелинейная емкость будет обозначаться С(u).

Если приложенное к емкости С(u) напряжение изменяется во времени, то ток через емкость можно определить с помощью одного из двух эквивалентных выражений:

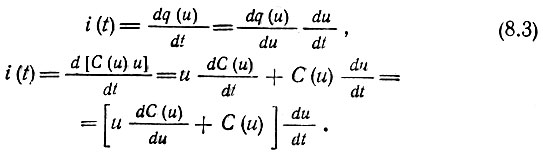
Если напряжение u изменяется в небольших пределах в окрестности точки u = U₀, то емкость можно представить в виде

Определенную таким образом емкость иногда называют дифференциальной.

На рис. 8.3 изображен примерный вид зависимости С(u) для емкости полупроводникового диода.

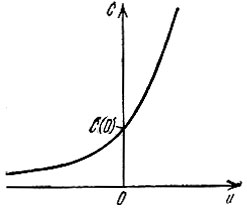
Рис. 8.3. Примерный вид вольт-фарадной характеристики полупроводникового диода

Наконец, катушка с ферромагнитным сердечником, обтекаемая сильным током, доводящим сердечник до магнитного насыщения, является примером нелинейной индуктивности L(i).

Соотношение между током i и напряжением u на индуктивности следует из исходного выражения для потокосцепления

Очевидно,

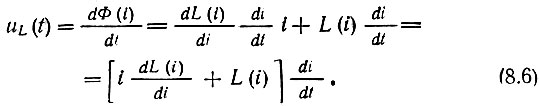
Если задано напряжение u_L(t) на индуктивности, то, очевидно,

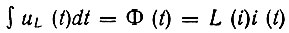
и, как и в случае линейной индуктивности,

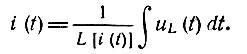
Под дифференциальной индуктивностью подразумевается величина

Понятиями дифференциальные сопротивление, емкость и индуктивность широко пользуются при рассмотрении воздействия относительно слабых сигналов на нелинейные элементы. При этом нелинейность элемента проявляется лишь в том, что величины R₀, С₀ и L₀ зависят от величины управляющего напряжения (или тока), определяющей положение рабочей точки на нелинейной характеристике. По отношению же к слабому сигналу подобный элемент является линейным устройством с переменным параметром (если управляющее напряжение изменяется во времени).

Свойства таких элементов рассматриваются в гл. 10.