8.2. Аппроксимация нелинейных характеристик

Для анализа и расчета нелинейных цепей необходимо задать вольт-амперные или иные аналогичные характеристики нелинейных элементов в аналитической форме.

Реальные характеристики обычно имеют сложный вид, затрудняющий точное их описание с помощью достаточно простого аналитического выражения.

В технике широкое распространение получили способы представления характеристик относительно простыми функциями, лишь приближенно отображающими истинные характеристики. Замена истинной характеристики приближенно представляющей ее функцией называется аппроксимацией характеристики.

Выбор оптимальной аппроксимации зависит от вида нелинейной характеристики, а также от режима работы нелинейного элемента Одним из наиболее распространенных способов аппроксимации является аппроксимация степенным полиномом.

Запишем аппроксимирующий степенной полином в форме

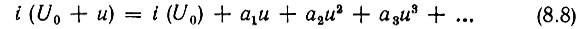
Если под нелинейным элементом подразумевается транзистор, то i - ток коллектора, а u - напряжение, например, между базой и эмиттером. Для вакуумного триода или пентода u - напряжение между управляющей сеткой и катодом, a i - анодный ток и т. д.

Коэффициенты a₁, а₂, а₃, ... определяются выражениями

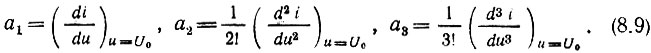
Нетрудно видеть, что а₁ представляет собой крутизну характеристики в точке u = U₀, а₂ - первую производную крутизны (с коэффициентом 1/2!), а₃ - вторую производную крутизны (с коэффициентом 1/3!) и т. д.

При заданной форме вольт-амперной характеристики величины коэффициентов а₁, а₂, а₃, ... существенно зависят от U₀, т. е. от положения рабочей точки на характеристике.

Рассмотрим некоторые типичные и важные для практики случаи.

1. Рабочая точка расположена на начальном участке характеристики, имеющем вид квадратичной параболы (рис. 8.4). Предполагается, что подводимое к нелинейному элементу напряжение сигнала е_s, накладываясь на постоянное напряжение Е₀ = U₀, не выходит за точку U₁, т. е. за начало характеристики.

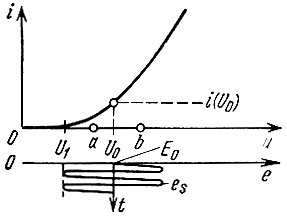
Рис. 8.4. Положение рабочей точки и пределы использования вольт-амперной характеристики (a, b), при которых применима аппроксимация полиномом второй степени

Выражение (8.8) в данном случае можно записать в виде полинома второй степени

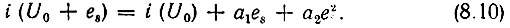
Коэффициент а₁, определяемый выражением (8.9), часто обозначается символом S (крутизна характеристики).

Коэффициент а₂ определяется из условия, что при 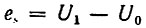ток i = 0, откуда вытекает уравнение

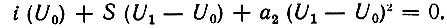
Таким образом,

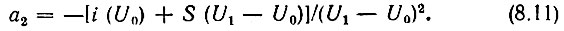
2. Рабочая точка является точкой перегиба характеристики, показанной на рис. 8.5.

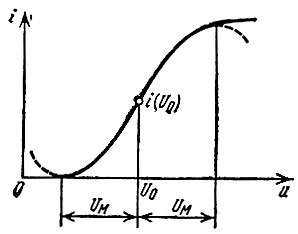
Рис. 8.5. Пример характеристики, для аппроксимации которой требуется полином третьей степени

В точке перегиба кривой i = f(u) все производные четного порядка равны нулю. Поэтому коэффициенты при четных степенях в выражении (8.8) обращаются в нуль и его можно записать в форме

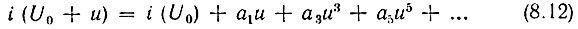
Для упрощения анализа часто ограничиваются полиномом всего лишь третьей степени без квадратичного члена (неполным полиномом третьей степени). Заменяя, как и в п. 1, u на напряжение сигнала е_s, получаем

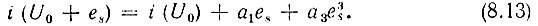
Соответствующая этой аппроксимации характеристика показана на рис. 8.5 штриховой линией. Напряжение U_M, соответствующее экстремумам аппроксимирующей функции и отсчитываемое от u = U₀, иногда называют напряжением насыщения. Заданием этого напряжения, а также а₁ (крутизны S в точке U₀) однозначно определяют коэффициент а₃ в выражении (8.13).

Действительно, в точке U₀ + U_M, т. е. при амплитуде входного сигнала равной U_M, выполняется тождество

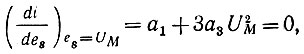
откуда

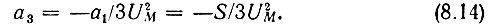
Отметим, что аппроксимацией (8.13) допустимо пользоваться, когда напряжение сигнала не выходит за пределы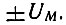

3. Рабочая точка находится на нижнем сгибе характеристики, изображенной на рис. 8.6.

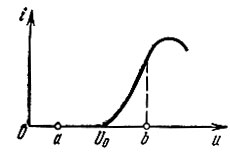
Рис. 8.6. Пример характеристики, для аппроксимации которой требуется полином высокой степени

Если изменение напряжения настолько велико, что используется участок, обозначенный на оси абсцисс буквами a, b, то для удовлетворительной аппроксимации требуется полином пятой или более высокой степени. При этом анализ сильно усложняется и применение степенного полинома для практических расчетов оказывается неэффективным.

При очень больших амплитудах сигнала часто оказывается удобным заменять реальную характеристику идеализированной, линейно-ломаной, составленной из отрезков прямых линий. Такое представление характеристики называется кусочно-линейной аппроксимацией. Некоторые примеры кусочно-линейной аппроксимации изображены на рис. 8.7. Рис. 8.7, а соответствует случаю, когда используется нижний сгиб и линейная часть характеристики (участок а-с); рис. 8.7, б - когда сигнал захватывает нижний и верхний сгибы (участок а-d), а рис. 8.7, в - когда сигнал достигает также и падающего участка характеристики (участок а-f). Следует особо подчеркнуть, что замена реальной нелинейной характеристики линейными отрезками не означает линеаризации цепи. Так, например, несмотря на то, что на участке b-с (рис. 8.7, а) характеристика линейна, по отношению к сигналу, захватывающему область изменения а-с, система в целом является существенно нелинейной.

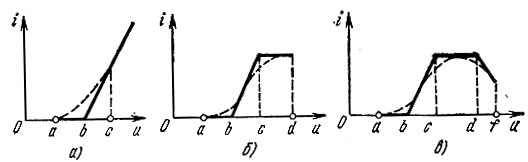
Рис. 8.7. Примеры кусочно-линейной аппроксимации характеристики при различных пределах ее использования

Кусочно-линейная аппроксимация особенно проста и удобна для исследований и расчетов, когда основное значение имеет нижний сгиб характеристики, т. е. когда можно ограничиваться двумя прямыми (рис. 8.7, а). При более сложной форме используемого участка характеристики число аппроксимирующих отрезков растет и кусочно-линейная аппроксимация теряет свои преимущества. В подобных случаях иногда для аппроксимации применяются различные трансцендентные функции, например гиперболический тангенс [4], экспоненциальные функции и некоторые другие.

Описанные выше приемы аппроксимации применимы и к соответствующим характеристикам реактивных нелинейных элементов.