
8.3. Воздействие гармонических колебаний на цепи с безынерционными нелинейными элементами
Основные свойства таких цепей можно выявить из анализа воздействия гармонических колебаний на резистивные элементы. В качестве такого элемента можно взять любой усилительный прибор с нелинейной вольт-амперной характеристикой.
Сначала рассмотрим режим работы, представленный на рис. 8.8, при котором напряжение сигнала es(t) не выходит за пределы точки U1 и вольт-амперная характеристика i(u) удовлетворительно аппроксимируется степенным полиномом (8.8). Подставив в (8.8) u = еs(t) = Е cos ω1t, получим
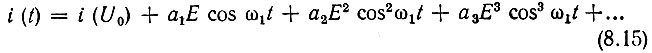
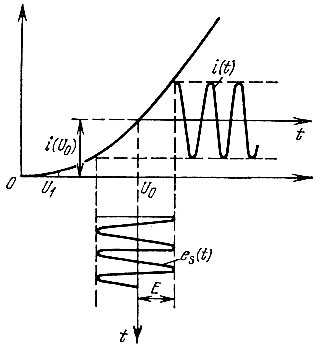
Рис. 8.8. Слабо-нелинейный режим работы усилительного прибора
Форма тока i(t) показана на рис. 8.8.
С помощью тригонометрических соотношений
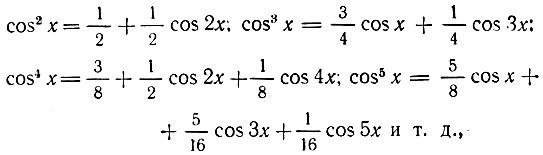
выражение (8.15) приводим к виду
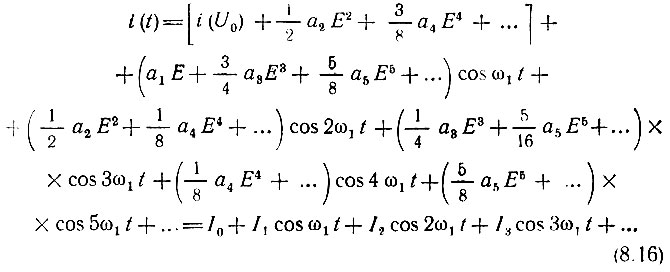
Из этого выражения видны следующие проявления нелинейности вольт-амперной характеристики при гармоническом воздействии:
- ток покоя i(U0) получает приращение, обусловленное, коэффициентами а2, а4, ... при четных степенях полинома (8.8):
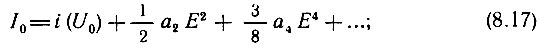
- амплитуда I1 гармоники основной частоты ω1 связана с амплитудой возбуждения Е нелинейным соотношением, обусловленным нечетными степенями полинома (8.8):
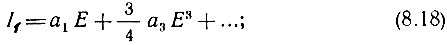
- ток i(t) содержит высшие гармоники с частотами nω1, кратными частоте воздействия ω1. Гармоники с частотами 2ω1, 4ω1, ... обусловлены четными степенями, а гармоники с частотами 3ω1, 5ω1, ... - нечетными степенями полинома (8.8).
Спектр тока при коэффициентах a1 = 2мА/В, а2 = 0,15 мА/В2, а3 = 0,03 мА/В3, i(U0) = 10 мА и амплитуде Е = 5 В показан на рис. 8.9. В данном примере всеми слагаемыми со степенью выше второй в выражении (8.15) можно пренебречь.
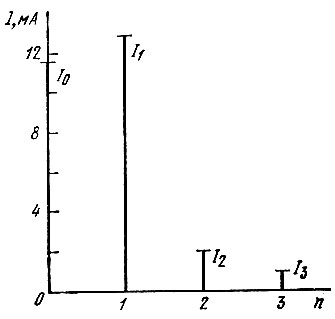
Рис. 8.9. Спектр тока в режиме, представленном на рис. 8.8
Рассмотрим теперь работу того же нелинейного элемента в режиме существенно более нелинейном (рис. 8.10, а), получаемом при сдвиге рабочей точки U0 влево и соответствующем увеличении амплитуды возбуждающего напряжения E. В данном случае целесообразно применить кусочно-линейную аппроксимацию волы амперной характеристики (см. § 8.2, комментарий к рис. 8.7, а).
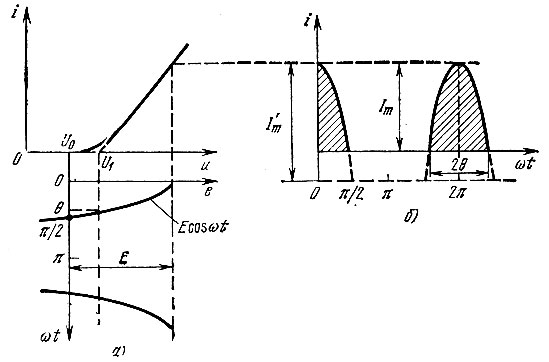
Рис. 8.10. Существенно нелинейный режим работы усилительного прибора
При гармоническом возбуждении ток i(t) приобретает импульсную форму (рис. 8.10, б). Угол θ, соответствующий изменению тока от максимального значения Im до нуля, получил название угла отсечки тока. Длительность импульсов тока равна 20 (рис. 8.10, б). Из рис. 8.10, а очевидно следующее выражение:

Амплитуда тока
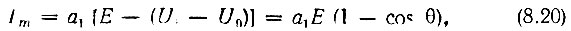
где а1 - крутизна линейной части вольт-амперной характеристики [см. выражение (8.9)].
При гармоническом возбуждении нелинейного элемента форма импульса тока в пределах -θ < ωt < θ близка к отсеченной косинусоиде и. если пренебречь кривизной вольт-амперной характеристики на нижнем сгибе (рис. 8.10, а), мгновенное значение тока можно выразить уравнением
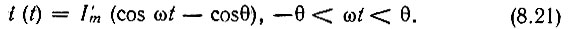
Символом 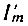 обозначено значение импульса, которое получилось бы при θ = π/2.
обозначено значение импульса, которое получилось бы при θ = π/2.
Так как амплитуда реального импульса Im соответствует моменту ωt = 0, имеет место соотношение
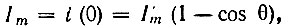
откуда
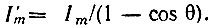
Подставив это выражение в (8.21), получим окончательно
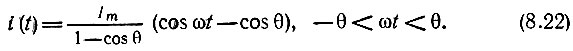
Основываясь на этом выражении нетрудно определить коэффициенты ряда Фурье для периодической последовательности импульсов, представленной на рис. 8.11. Ввиду четности функции i(t) относительно t [см. (8.22)] ряд содержит одни лишь косинусоидальные члены. Применяя формулы (2.24) и (2.32), находим
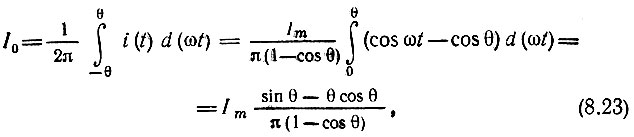
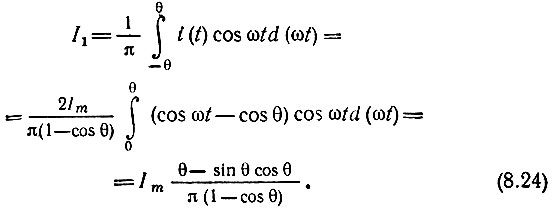
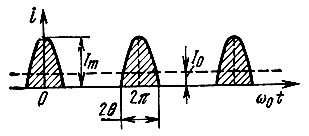
Рис. 8.11. Импульсный ток, соответствующий режиму, представленному на рис. 8.10
Аналогично можно получить общее выражение для амплитуды n-й гармоники
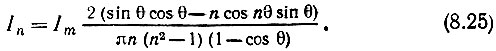
Отношения
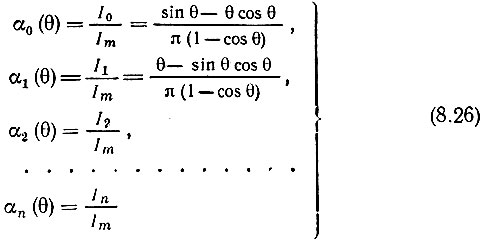
называются коэффициентами, соответственно, постоянной составляющей, первой гармоники и т. д. (функции Берга).
Графики коэффициентов α0, α1, α2, .... а также отношения γ = α1/α0 при изменении угла отсечки от θ = 0 до θ = 180° показаны на рис. 8.12. При θ = 0 ток вообще равен нулю (нелинейный элемент заперт на протяжении всего периода); при θ = 180° отсечка тока отсутствует и режим работы становится линейным. Спектр тока для нескольких значений угла отсечки представлен на рис. 8.13 (при Im = 1).
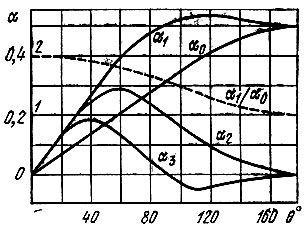
Рис. 8.12. Коэффициенты разложения импульсного тока в ряд Фурье в зависимости от угла отсечки θ
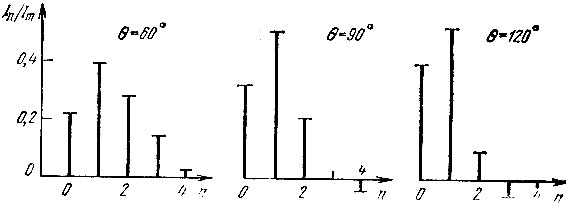
Рис. 8.13. Спектры импульсного тока при нескольких значениях угла отсечки θ
Из рассмотрения графиков функций αn(θ) и спектрограмм тока можно вывести важные заключения. Бросается в глаза, что при работе с углом отсечки меньше 180° отношение амплитуды первой гармоники I1 к постоянной составляющей I0 больше единицы, между тем как в линейном режиме это отношение много меньше единицы. Видно, что с уменьшением θ отношение

растет. Кроме того, с повышением номера гармоники максимумы функций αn(θ) перемещаются в область малых значений θ. Все эти обстоятельства оказывают существенное влияние на выбор режима работы нелинейного элемента при усилении колебаний, умножении частоты и на ряд других преобразований, которые изучаются в последующих параграфах данной главы.
Рассмотрим теперь воздействие на нелинейный резистивный элемент бигармонического колебания
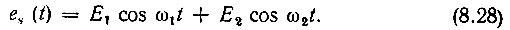
Для упрощения анализа ограничимся в данном параграфе рассмотрением слабо нелинейного режима (рис. 8.8), когда достаточно учитывать только линейный и квадратичный члены в полинома (8.8).
Подстановка (8.28) в ряд (8.8) приводит к следующим результатам:
- для линейного члена ряда
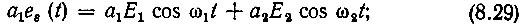
для квадратичного члена ряда
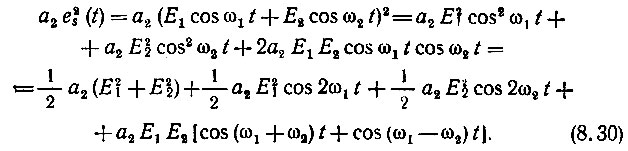
Первое слагаемое, не зависящее от времени, определяет приращение постоянного тока. Слагаемые с частотами 2ω1, и 2ω2 представляют собой вторые гармоники от соответствующих компонентов входного сигнала. Слагаемые же с частотами ω1 + ω2 и ω1 - ω2 представляют комбинационные колебания.
В более общем случае, проделав аналогичные преобразования над кубическим слагаемым a3e3s(t), убедимся, что это слагаемое вносит в спектр: ω1, ω2 - основные частоты; 3ω1, 3ω2 - третьи гармоники; 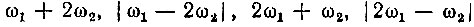 - комбинационные частоты.
- комбинационные частоты.
Продолжив подобный анализ для более высоких степеней ряда (8.8), можно показать, что при воздействии на нелинейное устройство бигармонического колебания в спектре на выходе нелинейности, описываемой полиномом k-й степени, могут присутствовать следующие частоты: ω = 0 - постоянная составляющая; ω = nω1, n = 1, 2, ..., k, - гармоники частоты ω2; ω = nω2, n = 1, 2, ..., k, - гармоники частоты ω2; 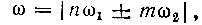 n = 1, 2, k и m = 1, 2, ..., k - комбинационные частоты (при условии, что n + m ≤ k).
n = 1, 2, k и m = 1, 2, ..., k - комбинационные частоты (при условии, что n + m ≤ k).
Спектрограмма колебания на входе и выходе нелинейного элемента, описываемого полиномом второй степени (k = 2), изображена на рис. 8.14. Из рисунка видно, что взаимодействие двух гармонических колебаний с неодинаковыми частотами в нелинейном устройстве второй степени приводит к возникновению разностной |ω1 - ω2| и суммарной ω1 + ω2 частот (помимо гармоник 2ω1 и 2ω2). Для практического использования этих новых частот достаточно применять на выходе нелинейного элемента линейную избирательную цепь, выделяющую полезную составляющую спектра (рис. 8.14, а).
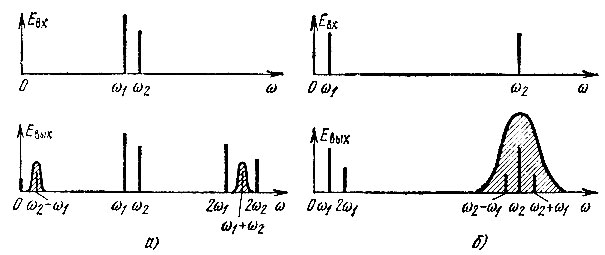
Рис. 8.14. Спектры колебания на входе и выходе квадратичного нелинейного элемента при бигармоническом воздействии с частотами ω1 и ω2: а - при близких частотах ω1 и ω2; б - при ω1 << ω2
Свойство квадратичного нелинейного элемента, позволяющее получить комбинационные частоты, широко применяется в радиотехнике для сдвига частоты сигнала.
В случае же 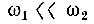 (рис. 8.14, б), когда комбинационные частоты
(рис. 8.14, б), когда комбинационные частоты 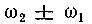 располагаются вблизи частоты ω2 и все три частоты: ω2, ω2 + ω1 и ω2 - ω1 могут быть выделены одним общим фильтром, можно получить спектр, соответствующий амплитудной модуляции колебания частоты ω2 относительно низкой частотой ω1. При нелинейности более высокого порядка (k > 2) можно осуществить выделение любой из частот вида
располагаются вблизи частоты ω2 и все три частоты: ω2, ω2 + ω1 и ω2 - ω1 могут быть выделены одним общим фильтром, можно получить спектр, соответствующий амплитудной модуляции колебания частоты ω2 относительно низкой частотой ω1. При нелинейности более высокого порядка (k > 2) можно осуществить выделение любой из частот вида 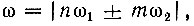 n + m ≤ k.
n + m ≤ k.
При более сложном составе входного спектра, содержащем частоты ω1, ω2, ω3 ..., на выходе нелинейного элемента возникают частоты nω1, nω2, nω3, ... и комбинационные частоты nωi ± mωk, где n и m - любые целые числа, а ωi и ωk - любая из пар частот входного спектра.
Нетрудно установить, что при любом сложном, но периодическом воздействии с основной частотой со на выходе нелинейного элемента имеет место также периодический процесс с основной частотой ω. Обогащение спектра в этом случае может произойти только за счет гармоник с частотами nω. Это объясняется тем, что в рассматриваемом частном случае все частоты выходного сигнала кратны частоте ω; следовательно, суммы и разности любых двух гармоник входного спектра также кратны ω.
Из приведенного ранее качественного рассмотрения видно, что простой резистивный нелинейный элемент в сочетании с избирательной линейной целью позволяет осуществить ряд преобразований, таких, как нелинейное резонансное усиление, умножение частоты колебания, выпрямление, детектирование модулированных колебаний, сдвиг частоты колебаний, амплитудная модуляция, и др. Этим вопросам посвящены § 8.4-8.12.
Воздействие гармонических колебаний на реактивные нелинейные элементы (емкость или индуктивность) рассматривается в гл. 10.

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
