12.2. Согласованная фильтрация заданного сигнала

Линейная фильтрация сигнала для выделения его из смеси сигнал + шум является одним из основных процессов, осуществляемых в любом радиоприемном устройстве. В основе фильтрации лежит использование частотной избирательности колебательных цепей. На протяжении первых 50-60 лет развития радиотехники к подобным частотным фильтрам предъявлялось требование возможно более равномерного пропускания спектра сигнала и возможно более полного подавления частот вне этого спектра. Идеальным считался фильтр с прямоугольной П-образной АЧХ.

С развитием теории информации и статистической теории обнаружения сигналов трактовка функций, которые должны выполняться линейным фильтром, а также подход к его построению существенно изменились.

Стало очевидным, что указанная выше трактовка обладает следующими двумя недостатками: 1) не учитывается форма сигнала (которая может быть различной при одной и той же ширине спектра сигнала); 2) не учитываются статистические свойства помехи. Поэтому даже идеальный фильтр с П-образной АЧХ фактически не согласован с сигналом и помехой и не дает на выходе максимально возможного отношения сигнал-помеха.

Коренной перелом в теории и практике линейной фильтрации связан с появлением работ Н. Винера, А. Н. Колмогорова, В. А. Котельникова и других ученых, которые поставили и решили задачу синтеза фильтра, оптимального по отношению к заданному сигналу, действующему на фоне помехи с заданными статистическими характеристиками.

В зависимости от того, какая из перечисленных в предыдущем параграфе задач решается, критерии оптимальности могут быть разными. Для задачи обнаружения сигнала в шумах наибольшее распространение получил критерий максимума отношения сигнал-помеха на выходе фильтра. Фильтры, отвечающие этому критерию, называются согласованными. В настоящей главе рассматриваются только такие фильтры.

Требования к фильтру, максимизирующему отношение сигнал- помеха, можно сформулировать следующим образом. На вход линейного четырехполюсника с постоянными параметрами и передаточной функцией К(iω) подается аддитивная смесь сигнала s(t) и шума n(t) (рис. 12.1). Сигнал полностью известен; это означает, что заданы его форма и положение на оси времени. Шум представляет собой вероятностный процесс с заданными статистическими характеристиками. Требуется синтезировать фильтр, обеспечивающий получение на выходе наибольшего возможного отношения пикового значения сигнала к среднеквадратическому значению шума. При этом не ставится условие сохранения формы сигнала, так как для обнаружения его в шумах форма значения не имеет.

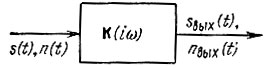
Рис. 12.1. Воздействие сигнала и помехи на линейный четырехполюсник

Для уяснения сути согласованной фильтрации сигнала сначала рассмотрим наиболее простой случай, когда на входе фильтра с равномерной АЧХ имеется один лишь полезный сигнал s(t) с известным спектром 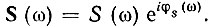Требуется найти фазочастотную характеристику фильтра, при которой обеспечивается максимизация пика сигнала на выходе фильтра. Напомним, что спектральная плотность S(ω) сигнала полностью определяет его энергию Э. Любое изменение фазовых соотношений в спектре не оказывает влияния на энергию сигнала (см. § 2.8). Поэтому поставленная выше задача равносильна задаче максимизации пика сигнала при заданной энергии входного сигнала.

Представим выходной сигнал в виде

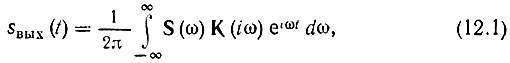
где

- передаточная функция неминимально-фазового четырехполюсника с искомой фазочастотной характеристикой φ_К(ω) и с равномерной амплитудно-частотной характеристикой К₀ = const.

Таким образом,

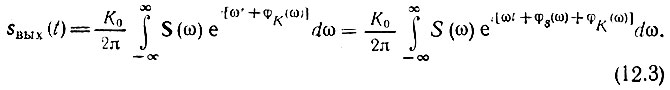
Основываясь на очевидном неравенстве

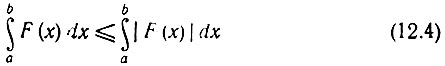
и учитывая, что 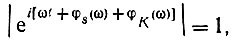можно составить следующее неравенство:

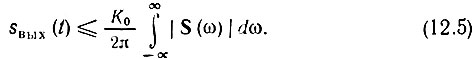
Это неравенство определяет верхний предел мгновенного значения колебания s_вых(t) при заданном спектре входного сигнала. Максимизация пика выходного колебания получается при обращении неравенства (12.5) в равенство, а для этого необходимо, как это вытекает из сопоставления выражений (12.3) и (12.5), обеспечить определенное соотношение между фазовой характеристикой фильтра φ_К(ω) и фазовой характеристикой спектра φ_s(ω) входного сигнала.

Допустим, что выходной сигнал достигает максимума в момент t₀ (пока еще неопределенный). Тогда выражение (12.3) дает

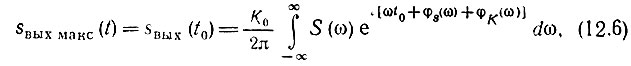
а условие обращения неравенства (12.5) в равенство сводится к следующему:

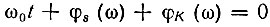
или

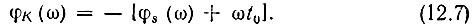
Это соотношение можно назвать условием компенсации начальных фаз в спектре сигнала. Действительно, первое слагаемое в правой части (12.7), равное - φ_s(ω), компенсирует фазовую характеристику φ_s(ω) входного спектра S(ω). В результате прохождения сигнала через фильтр с фазовой характеристикой φ_К(ω) сложение всех компонентов спектра, скорректированных по фазе, образует пик выходного сигнала в момент времени t = t₀.

Связь между фазовой характеристикой φ_s(ω) входного спектра, компенсирующей ее характеристикой - φ_s(ω) и полной фазовой характеристикой фильтра φ_К(ω) = - [φ_s(ω) + ω₀t₀] поясняется рис. 12.2.

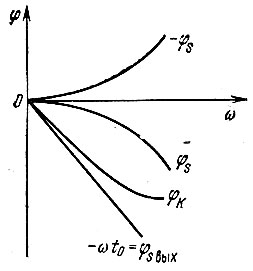
Рис. 12.2. Соотношение между фазовыми характеристиками спектра сигнала на входе и выходе согласованного фильтра

После прохождения через фильтр спектр выходного сигнала будет иметь фазовую характеристику

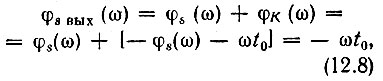
показанную на том же рисунке.

Смысл и минимально возможное значение t₀ подробнее рассматриваются в следующем параграфе, однако из простых физических представлений очевидно, что для образования пика требуется использование всей энергии сигнала, а это возможно не ранее окончания действия входного сигнала. Иными словами, задержка t₀ не может быть меньше, чем полная длительность сигнала.

Введем теперь в рассмотрение помеху на входе фильтра. При равномерном энергетическом спектре помехи (белый шум) W(ω) = W₀ = const - фильтр с равномерной АЧХ совершенно неприемлем, так как мощность помехи на выходе достигает очень большой величины (теоретически бесконечно большой).

Для отыскания оптимальной передаточной функции, максимизирующей отношение сигнал - помеха на выходе фильтра, составим выражения для сигнала и шума сначала отдельно, а затем в виде их отношения.

Пиковое значение сигнала определим выражением

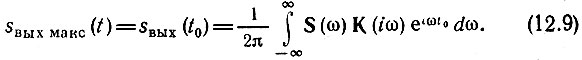
Среднеквадратическое значение помехи на выходе фильтра

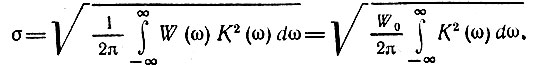
Следовательно, отношение пикового значения сигнала к среднеквадратическому значению помехи на выходе фильтра

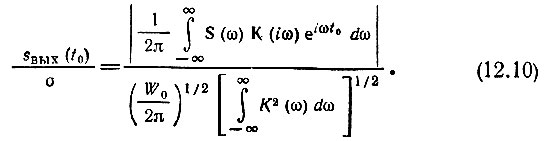
Воспользуемся известным неравенством Шварца

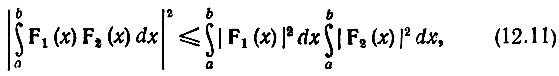
где F₁(х) и F₂(х) - в общем случае комплексные функции.

Это неравенство обращается в равенство только при выполнении условия

т. е. когда F₂(х) пропорциональна функции, комплексно-сопряженной F₁(х) (А - произвольный постоянный коэффициент).

Используя обозначения выражения (12.9), приравнивая S(ω) = F₁(iω) и К(iω) е^iωt₀ = F₂(iω), можем переписать выражение (12.11) в форме

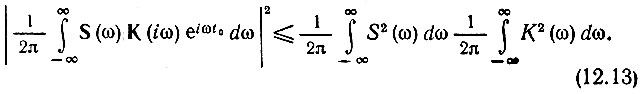
Следовательно, определяемая выражением (12.10) величина s_вых(t₀)/σ отвечает условию

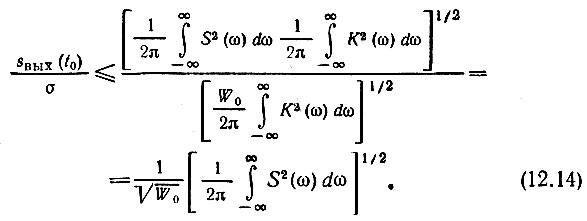
Учитывая, что выражение в квадратных скобках есть не что иное, как полная энергия входного сигнала Э [см. (2.66)], запишем последнее выражение в форме

Наконец, из выражения (12.12) следует, что это неравенство обращается в равенство при выполнении условия

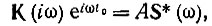
откуда

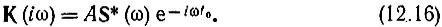
Полученное соотношение полностью определяет передаточную функцию, максимизирующую отношение сигнал - помеха на выходе фильтра.

Учитывая, что 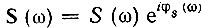, а комплексно-сопряженная функция 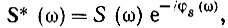перепишем выражение (12.16) еще и в такой форме:

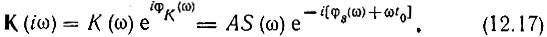
Из этого соотношения вытекают два условия для фазовой и амплитудной характеристик согласованного фильтра:

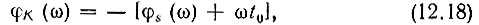
В тех случаях, когда под комплексной передаточной функцией подразумевается безразмерная величина (например, отношение комплексных амплитуд напряжения на выходе и входе), коэффициент А должен иметь размерность, обратную размерности спектральной плотности сигнала.

Соотношения (12.18), (12.19) имеют глубокий физический смысл. Первое из них, совпадающее с (12.7) и определяющее компенсацию начальных фаз в спектре сигнала, было истолковано выше. Соотношение (12.19), устанавливающее, что модуль передаточной функции К(ω) должен по своей форме совпадать с модулем спектральной плотности сигнала S(ω), также легко поддается физическому истолкованию. При АЧХ К(ω), отвечающей условию (12.19), фильтр пропускает спектральные составляющие шума неравномерно, с тем большим ослаблением, чем меньше модуль S(ω). Это приводит к существенному уменьшению мощности шума на выходе фильтра. На рис. 19.3, б эта мощность определяется площадью (заштрихованной) под кривой W_вых(ω) = К²(ω) W₀. (Для наглядности характеристики на рис. 12.3 построены в предположении, что AS(0) = 1.)

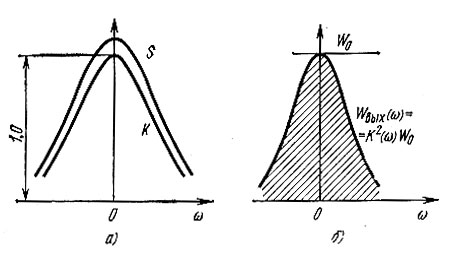
Рис. 12.3. Спектральная плотность сигнала и АЧХ согласованного фильтра (а) и энергетические спектры на входе и выходе (б)

Ослабление сигнала из-за неравномерности характеристики К(ω) выражено в меньшей степени, чем ослабление шума, поскольку уменьшение К(ω) имеет место для спектральных составляющих, вклад которых в величину пика сигнала сравнительно мал. В результате получается ослабление шума относительно сигнала. В сочетании с фазовой компенсацией спектра сигнала (на дисперсию выходного шума эта компенсация не оказывает влияния) это и приводит к максимизации отношения сигнал-помеха на выходе фильтра.