12.3. Импульсная характеристика согласованного фильтра. Физическая осуществимость

Тот факт, что коэффициент передачи согласованного фильтра К(iω) является функцией, сопряженной по отношению к спектру сигнала S(ω), указывает на существование тесной связи также и между временными характеристиками фильтра и сигнала. Для выявления этой связи найдем импульсную характеристику согласованного фильтра.

Применяя выражение (5.28) и учитывая формулу (12.16), получаем

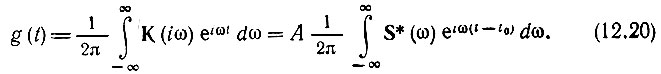
Учитывая, что

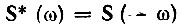
и переходя к новой переменной ω₁ = -ω, переписываем выражение (12.20) следующим образом:

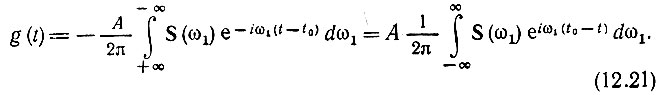
Правая часть этого выражения есть не что иное, как функция As(t₀ - t). Следовательно, если задан сигнал s(t), то импульсная характеристика согласованного (оптимального) фильтра g(t) определяется как функция

Построение графика функции s(t₀ - t) показано на рис. 12.4. Кривая s(-t) является зеркальным отражением заданного сигнала s(t) с осью ординат в качестве оси симметрии. Функция же s(t₀ - t), сдвинутая относительно s(-t) на величину t₀ вправо, также зеркальна по отношению к исходному сигналу s(t), но с осью симметрии, проходящей через точку t₀/2 на оси абсцисс. На рис. 12.5 показано аналогичное построение для случая, когда отсчет времени ведется от начала сигнала.

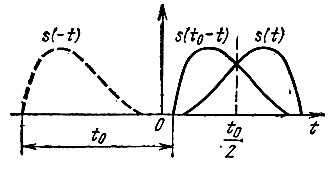
Рис. 12.4. Построение функции, зеркальной по отношению к сигналу

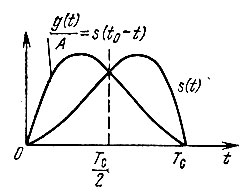
Рис. 12.5. Построение импульсной характеристики согласованного фильтра

Поскольку импульсная характеристика физической цепи не может начинаться при t < 0 [отклик фильтра не может опережать воздействие δ(t)], то очевидно, что задержка t₀, фигурирующая в выражении (12.16), не может быть меньше, чем Т_с. Только при t₀ ≥ Т_с может быть использована вся энергия сигнала для создания наибольшего возможного пика в точке t - t₀. Ясно, что увеличение t₀ сверх Т_с не влияет на величину пика выходного сигнала, а просто сдвигает его вправо (в сторону запаздывания).

С другой стороны, условие t₀ ≥ Т_с накладывает на сигнал s(t) требование, чтобы длительность его Т_с была конечна; только в этом случае при конечной величине задержки t₀; можно реализовать пик сигнала. Иными словами, применение согласованной фильтрации для максимизации отношения сигнал - помеха в описанном выше смысле возможно при импульсном сигнале (а также ограниченной по продолжительности пачке импульсов).

Обратимся к вопросу о физической осуществимости согласованного фильтра. Пусть задан произвольный сигнал s(t), которому соответствуют импульсная характеристика согласованного фильтра g(t) и фурье-преобразование от этой функции К(iω), определяемые соответственно выражениями (12.22) и (12.16). Возникает вопрос, при каких условиях К(iω) может являться передаточной функцией физически осуществимого четырехполюсника.

Ответ на этот вопрос дает критерий осуществимости Пэли - Винера, согласно которому неравенство

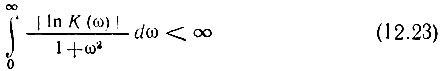
является необходимым условием, чтобы положительная функция К(ω) могла быть модулем передаточной функции пассивной электрической цепи. Так как в рассматриваемой задаче К(ω) = AS(ω) [см. (12.19)], то условие (12.23) можно записать в виде^*

^* (Здесь под ω подразумевается безразмерная величина.)

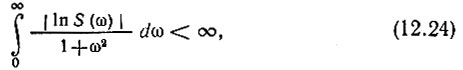
т. е. необходимо, чтобы интеграл (12.24) сходился.

Нужно подчеркнуть, что условие (12.24) является необходимым, но недостаточным. По существу, условие (12.24) сводится к требованию, чтобы длительность сигнала s(t) была ограничена. Так, например, при спектре сигнала, определяемом выражением (2.82) [см. рис. 2.20, б), функция времени s(t) неограничена во времени и такова же требуемая импульсная характеристика согласованного фильтра g(t) = As(t₀ - t), которую невозможно реализовать. Интеграл (12.24) в этом случае расходится, так как вне интервала (-ω_m, ω_m) функция S(ω) равна нулю, а |lnS(ω)| обращается в бесконечность.

Хотя критерий Пэли - Винера оставляет открытым вопрос о структуре цепи, из него вытекают некоторые полезные следствия о свойствах осуществимых цепей.

В частности, из него следует, что АЧХ К(ω) должна быть интегрируемой в квадрате, т. е. 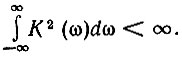Далее, АЧХ К(ω) может быть равной нулю только на некоторых дискретных частотах, но не в конечной полосе частот. Действительно, если в полосе ω₁ < ω < ω₂ функция К(ω) = 0, то |lnK(ω)| обращается в бесконечность и, как об этом уже упоминалось выше, интеграл расходится, т. е. условие (12.23) не выполняется. Из этого следует, что фильтры с П-образной АЧХ нереализуемы, хотя практически можно получить характеристики, очень близкие к идеальным.

Очевидно также, что передаточная функция К(ω) = Ке^-αω, ω > 0, реализуема, так как |lnK(ω)| = |lnK - αω| растет медленнее, чем знаменатель в (12.23), т. е. условие (12.23) выполняется. Гауссов же фильтре передаточной функцией К(ω) = Ке^-αω2 не реализуется, так как |ln K(ω)| = |ln K - αω²| растет с увеличением ω с такой же скоростью, что и знаменатель в (12.23).