12.4. Сигнал и помеха на выходе согласованного фильтра

Для определения формы сигнала на выходе используем общее выражение

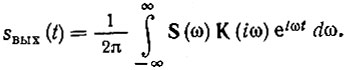
Подставив в него соотношение (12.16), получим

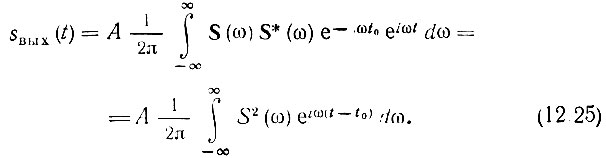
При t = t₀ это выражение переходит в

где Э - энергия входного сигнала.

С другой стороны, из первой части соотношения (12.25), в которой фигурирует произведение спектральных плотностей S(ω) и S*(ω)e^-iωt₀ вытекает, что s_вых(t) можно представить как свертку следующих двух функций времени: s(t) и s(t₀ - t).

Таким образом,

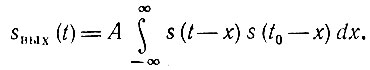
Сделаем подстановку 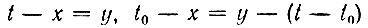Тогда

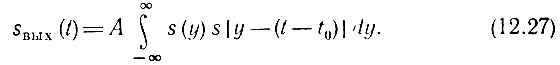
Нетрудно видеть, что интеграл в правой части этого выражения есть не что иное, как корреляционная функция входного сигнала В_s(t - t₀). Таким образом, приходим к важному выводу, что

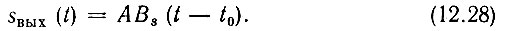
Итак, сигнал на выходе согласованного фильтра с точностью до постоянного коэффициента А совпадает с корреляционной функцией входного сигнала.

Для построения графика функции s_вых(t) по заданной функции B_s(τ) достаточно в последней τ заменить t - t₀ (и учесть коэффициент А). При t = t₀, т. е. при τ = 0, величина В_s(0) равна энергии сигнала. Следовательно, как и при спектральном рассмотрении, пиковое значение сигнала [см. (12.26)]

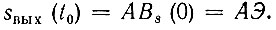
Рассмотрим теперь параметры и статистические характеристики шума на выходе согласованного фильтра. При действии белого шума с нормальным законом распределения (именно такой шум и представляет основной интерес для практики) распределение шума на выходе линейного фильтра остается нормальным. Энергетический спектр шума на выходе, как это ясно из (7.1) и рис. 12.3, равен W_вых(ω) = К²(ω)W₀. Следовательно, корреляционная функция шума на выходе согласованного фильтра

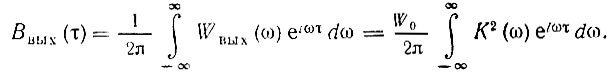
Подставляя К(ω) = AS(ω) и учитывая выражения (12,25) и (12,28), в которых обозначим t - t₀ = τ, получаем

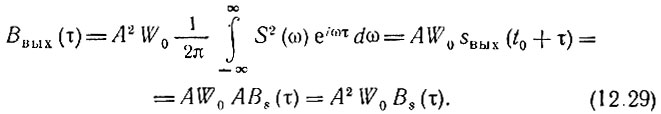
Отсюда следует, что корреляционная функция шума на выходе согласованного фильтра по форме совпадает с корреляционной функцией входного сигнала (и, следовательно, с выходным сигналом).

Приравнивая τ = 0, находим дисперсию (среднюю мощность) шума на выходе

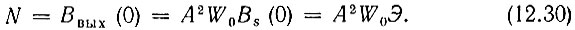
Составим отношение пикового значения сигнала s_вых(t) к среднеквадратическому значению шума В соответствии с формулами (12.26) и (12.30)

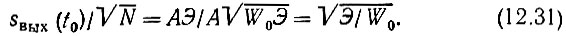
Итак, при белом шуме отношение сигнал-шум на выходе фильтра, согласованного с сигналом, зависит только от энергии сигнала и энергетического спектра шума W₀.

Из этого заключения следует, что при заданных энергии и ширине спектра сигналу можно придавать различную форму, выгодную для решения конкретной задачи.

Так, для повышения скрытности передачи целесообразно удлинять сигнал при соответствующем уменьшении амплитуды (А²₀Т_с = const). Это приводит к уменьшению отношения сигнал-помеха на входах любых радиоприемных устройств, что затрудняет извлечение информации из смеси сигнал + шум. Лишь в приемнике с фильтром, согласованным с данным сигналом, восстанавливается наибольшее возможное при заданной энергии отношение сигнал-помеха. Следует, конечно, обеспечить неизменную ширину спектра при удлинении сигнала. Это можно осуществить, введя внутриимпульсную модуляцию, например частотную [2]. Пример подобного сигнала - импульса с линейной частотной модуляцией (ЛЧМ импульс) был рассмотрен в § 3.7, п.3.

Удлинение радиоимпульса, дополняемое внутриимпульсной модуляцией, позволяет также снизить пиковую мощность генератора в передатчике при заданной энергии сигнала и при сохранении разрешающей способности сигнала (после сжатия в согласованном фильтре). Это преимущество более подробно рассматривается в § 12.5, п.2.