12.5. Примеры построения согласованных фильтров

1. Сигнал в виде прямоугольного видеоимпульса

Зададим сигнал следующей функцией времени:

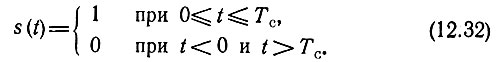
Спектральная плотность такого сигнала, как известно,

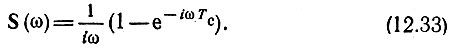
По формуле (12.16), в которой t₀ приравниваем длительности импульса Т_с, находим передаточную функцию согласованного фильтра

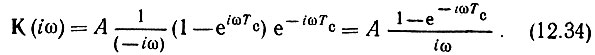
Рассматриваемый пример характерен тем, что К(iω) отличается от спектра сигнала S(ω) лишь постоянным коэффициентом. Ясно, что и импульсная характеристика фильтра g(t) совпадает по форме с самим сигналом s(t); действительно, из соотношения (12.22) следует, что

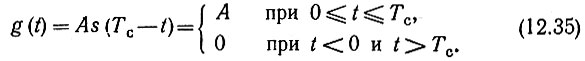
График g(t)/A (рис. 12.6) по форме полностью совпадает с входным импульсом s(t).

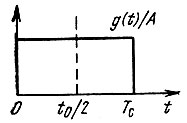
Рис. 12.6. Импульсная характеристика фильтра, согласованного с прямоугольным импульсом

Дальнейшая задача сводится к отысканию структуры физической цепи, обладающей импульсной характеристикой, изображенной на рис. 12.6, и передаточной функцией, определяемой формулой (12.34).

Простейший сигнал (12.32) удобен для иллюстрации основных положений синтеза четырехполюсника по заданной импульсной характеристике g(t) = As(t₀ - t), или, что то же, по комплексной передаточной функции К(iω), являющейся фурье-преобразованием от g(t).

Прежде всего отметим, что интеграл

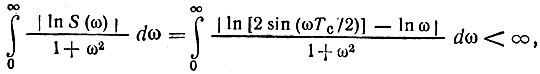
т. е. интеграл сходится, так что функция К(ω) = AS(ω) не противоречит критерию Пэли-Винера (12.23).

Для выяснения возможности реализации требуемой передаточной функции (12.34) с помощью четырехполюсника с сосредоточенными параметрами рассмотрим свойства этой функции на р-плоскости:

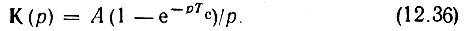
Эта функция не имеет полюсов, так как в точке р = 0 числитель также обращается в нуль; число же нулей функции К(р), являющихся корнями уравнения 1 - е^-рT_с = 0 и равных p_k = k(2π/Т_с), бесконечно велико. Из этого следует, что для реализации функции (12.34) требуется система с распределенными параметрами - отрезок линии с временем пробега вдоль линии, равным Т_с. К этому выводу нетрудно придти, рассмотрев непосредственно функцию (12.34). Очевидно, что структурная схема должна иметь вид, представленный на рис. 12.7. Первый множитель 1/iω реализуется интегрирующим звеном, а второй 1 - е^-iωТ_с устройством вычитания, к которому сигнал попадает без задержки и с задержкой Т_с. Передаточная функция идеальной линии задержки (без потерь) равна е^-iωT_с.

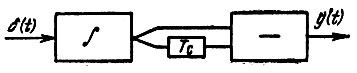
Рис. 12.7. Структурная схема фильтра, согласованного с прямоугольным импульсом

Объяснить работу этой схемы можно также и с помощью рассуждений, основанных на временных представлениях: при подаче на вход единичного импульса э. д. с. [дельта-функции δ(t)] на выходе идеального интегратора развивается постоянное напряжение, начинающееся с момента t = 0. На выходе устройства получается напряжение в виде разности двух единичных скачков, сдвинутых относительно друг друга на время Т_с (рис. 12.8, а).

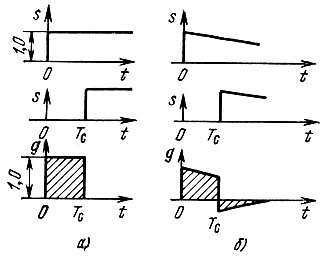
Рис. 12.8. Формирование импульсной характеристики в идеальном (а) и физическом фильтре (б)

Реализация изображенного на рис. 12.7 устройства, которое обеспечивало бы точное интегрирование, а также задержку входного сигнала без искажения его формы (в пределах бесконечно широкого спектра единичного импульса), практически неосуществима. Можно, однако, получить достаточно хорошее приближение при использовании реальной интегрирующей RC-цепи, если обеспечить постоянную времени этой цепи, достаточно большую по сравнению с длительностью Т_с. Получающийся при этом на выходе вычитающего устройства импульс напряжения, являющийся разностью двух экспонент (рис. 12.8, б), может быть сделан достаточно близким к прямоугольному.

Найдем напряжение на выходе фильтра. Применяя формулу (12.28) и учитывая, что корреляционная функция прямоугольного импульса имеет вид равнобедренного треугольника с основанием 2Т_с и высотой, равной величине энергии импульса, получаем

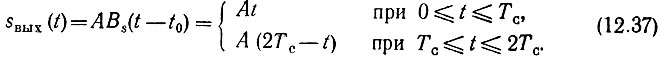
(В данном случае, при единичной амплитуде, энергия Э = T_с).

Максимальное значение выходного сигнала, равное АТ_с, достигается в момент t = Т_с, т. е. к концу действия входного сигнала (рис. 12.9).

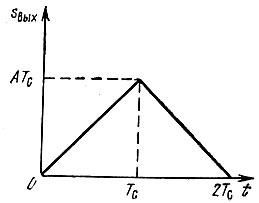
Рис. 12.9. Сигнал на выходе фильтра, согласованного с прямоугольным импульсом

Отношение сигнал-помеха в соответствии с формулой (12.31)

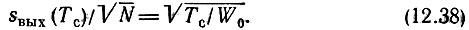
Для сравнения составим аналогичное отношение сигнал-помеха для несогласованного фильтра, выполненного в виде одного RС-звена с передаточной функцией

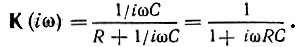
Максимальное значение выходного сигнала, достигаемое к моменту t = Т_с, равно 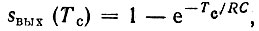а среднеквадратическое значение шума

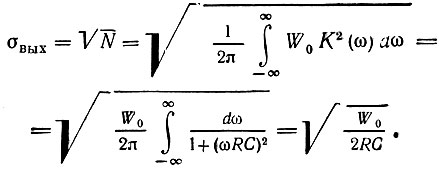
Таким образом

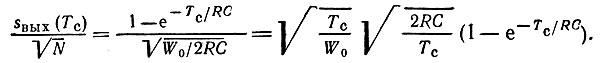
При Т_с/RC = 1,28 произведение 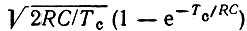достигает максимального значения, равного ∼0,77. Таким образом, переход от однозвенного фильтра к согласованному с сигналом фильтру дает в данном примере увеличение отношения сигнал - помеха в 1/0,77 = 1,3 раза (2,2 дБ).

Как будет видно из дальнейших примеров, технические преимущества согласованной фильтрации существенно проявляются при более сложных сигналах.

2. Радиоимпульс с частотно-модулированным заполнением

Рассмотрим сигнал, изображенный на рис. 12.10, а. Огибающая этого сигнала имеет прямоугольную форму, а частота заполнения изменяется по линейному закону (рис. 12.10, б) со скоростью

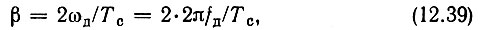
где Т_с - длительность импульса; 2ω_д - полное изменение частоты внутри импульса; ω₀ = 2πf₀ - центральная частота заполнения. В дальнейшем исходим из условия, что 2ω_д << ω₀. Таким образом,

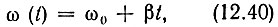
а мгновенное значение сигнала в интервале от -Т_с/2 до Т_с/2 определяется выражением

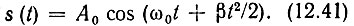
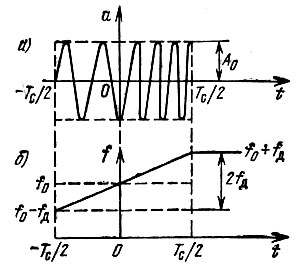
Рис. 12.10. ЛЧМ импульс (а) и закон изменения мгновенной частоты (б)

Спектральная плотность подобного импульса была определена в гл. 3. Было установлено, что модуль и фаза спектральной плотности определяются следующими выражениями [см. (3.50) и (3.51)]:

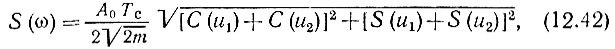
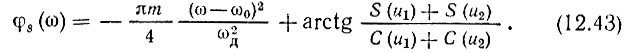
В этих выражениях S(x) и C(x) - интегралы Френнеля [см. выражение (3.49)], а u₁, u₂ и m определяются формулами

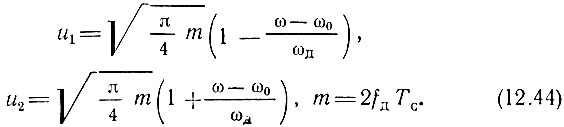
Выражения (12.42), (12.43) могут быть в принципе положены в основу синтезирования фильтра, но создание четырехполюсника, точно реализующего столь сложные амплитудную и фазовую характеристики, представляет собой задачу трудную или даже вообще невыполнимую. Поэтому приходится прибегать к различным приемам аппроксимации амплитудно-частотной и фазовой характеристик. Первым этапом на этом пути является допущение о том, что огибающая спектра сигнала имеет прямоугольную форму, а фазовая характеристика - форму квадратичной параболы. Таким образом, точные выражения (12.42) и (12.43) заменяются приближенными [см. пояснения к формулам (3.50) и (3.51)]:

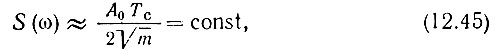
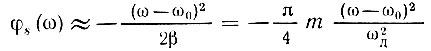
при ω₀ - ω_д < ω < ω₀ + ω_д.

В § 3.7 было показано, что такое приближение тем лучше, чем больше величина m = 2f_дT_с (постоянный фазовый сдвиг π/4 опущен).

При отсчете времени t от начала импульса фазовую характеристику спектра сигнала запишем в виде

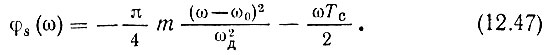
Для сигнала с подобными амплитудными и фазовыми спектрами согласованный фильтр должен обладать прямоугольной амплитудно-частотной характеристикой и фазочастотной характеристикой, определяемой выражением

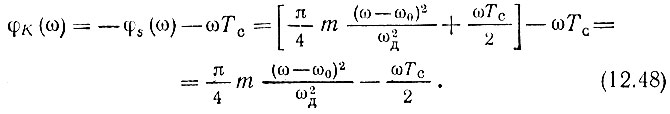
Строго прямоугольная АЧХ также неосуществима. Поэтому дальнейшее упрощение заключается в замене прямоугольной амплитудной характеристики фильтра обычной характеристикой резонансного фильтра. После этого фильтр может быть осуществлен в виде сочетания двух линейных четырехполюсников: полосового резонансного фильтра (обычный усилитель промежуточной частоты приемника) и специального четырехполюсника с равномерной амплитудной и квадратичной фазовой характеристиками.

Заметим, что фазовой характеристике (12.48) соответствует временная задержка

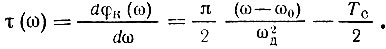
В качестве устройства с требуемой фазовой характеристикой может быть использована любая цепь, у которой задержка в некотором частотном диапазоне (вблизи частоты ω₀) линейно зависит от частоты. Такими свойствами обладают дисперсионные линии задержки с поверхностной волной.

Определим сигнал на выходе фильтра. При этом будем иметь в виду не аппроксимированный, а точный согласованный фильтр, передаточная функция которого отвечает условию (12.16).

Основываясь на соотношении (12.28), воспользуемся выражением (3.106') для корреляционной функции входного сигнала, выведенным в § 3.11:

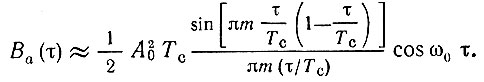
Заменяя в этом выражении τ на t - Т_с и ограничиваясь рассмотрением участка вблизи точки t - Т_с, т. е. в окрестности точки, где выходной сигнал достигает пикового значения, можем считать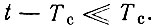

Тогда

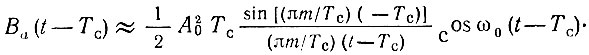
Учитывая, что m = (1/π)ω_дТ_с [см. формулу (3.38)], последнее выражение перепишем в несколько иной форме

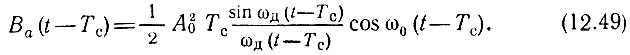
Подставляя полученное выражение в (12.28), находим напряжение на выходе согласованного фильтра

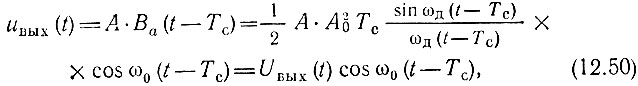
где огибающая

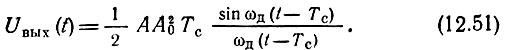
Заметим, что частота заполнения смодулирована и равна ω₀, т. е. средней частоте входного сигнала.

Если фильтр свободен от потерь, то энергия сигнала на выходе будет равна энергии сигнала на входе. При этом условии должно выполняться равенство

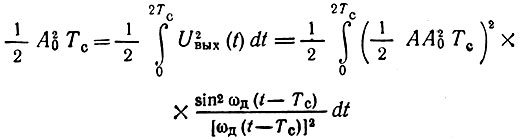
или

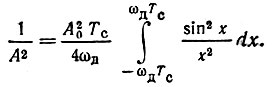
При больших значениях параметра m = 2f_дТ_с пределы интегрирования 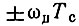можно заменить на 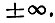Тогда интеграл равен π и окончательно

Подставляя (12.52) в выражение (12.51), получаем

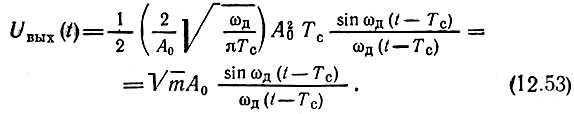
Сигналы на входе и выходе фильтра изображены на рис. 12.11 (при А₀ = 1). Наибольшая амплитуда выходного сигнала (в момент 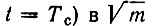раз больше, чем на входе, а длительность основного лепестка, отсчитываемого между двумя нулями, равна 1/f_д. При определении длительности выходного импульса на уровне 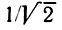от максимального значения получается приблизительно вдвое меньшая величина, а именно Т_{с вых} ≈ 1/2f_д.

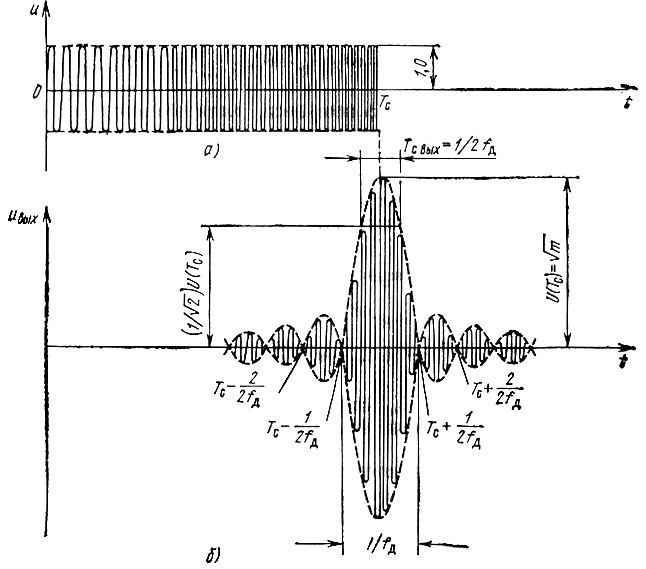
Рис. 12.11. ЛЧМ импульс на входе согласованного фильтра (а) и сжатый сигнал на выходе (б)

Таким образом, отношение

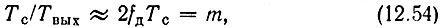
совпадающее по величине с параметром модуляции m = 2f_дT_с, можно назвать коэффициентом сжатия частотно-модулированного импульса в оптимальном фильтре.

Из выражения (12.53) видно, что компенсация фаз спектра сигнала, составляющая сущность согласованной фильтрации, приводит в рассматриваемом примере к сокращению длительности импульса в m раз при одновременном увеличении амплитуды сигнала в 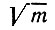раз. Это обстоятельство является весьма ценным для практики, так как позволяет удлинять импульс, генерируемый передатчиком, для увеличения энергии сигнала без потери разрешающей способности, которая определяется длительностью импульса на выходе согласованного фильтра [2]. Техническое преимущество этого метода проявляется особенно в тех случаях, когда увеличение амплитуды импульсов в передатчике ограничивается импульсной мощностью электронных приборов, используемых для генерации колебаний. Значительно проще повышать энергию сигнала удлинением импульсов при одновременном наложении частотной модуляции. При этом величина параметра модуляции m должна расти пропорционально длительности Т_с излучаемого сигнала (при заданной длительности T_{с вых} импульса на выходе согласованного фильтра). Иными словами, девиация частоты должна оставаться неизменной, а скорость изменения частоты β должна быть обратно пропорциональна величине Т_с (см. § 12.4).

3. Пачка одинаковых импульсов

Рассмотрим сигнал в виде группы из n одинаковых видеоимпульсов (рис. 12.12). Интервалы между импульсами могут быть неодинаковыми. Спектр такого сигнала

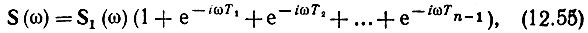
где S₁(ω) - спектр первого импульса, начинающегося в момент t = 0; S₁(ω) е^-iωТ₁ - спектр второго импульса, начинающегося в момент t = Т₁, и т. д.

Рис. 12.12. Сигнал в виде пачки импульсов

Так как полная длительность изображенного на рис. 12.12 сигнала равна τ_и + Т_n-1 то в соответствии с выражением (12.16) согласованный со спектром S(ω) фильтр должен обладать коэффициентом передачи

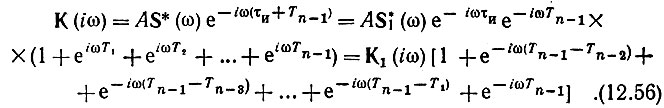
В этом выражении 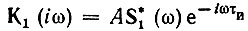представляет собой коэффициент передачи фильтра, согласованного с одиночным импульсом.

Основываясь на выражении (12.56), нетрудно наметить схему фильтра, согласованного с сигналом, изображенным на рис. 12.12. Подобный фильтр должен содержать звено с передаточной функцией К₁(iω), обеспечивающее оптимальную внутриимпульсную обработку сигнала, и набор линий задержек. Величины этих задержек должны нарастать в порядке, обратном расстановке импульсов в пачке на входе фильтра. Один из возможных вариантов такого устройства показан на рис. 12.13, а.

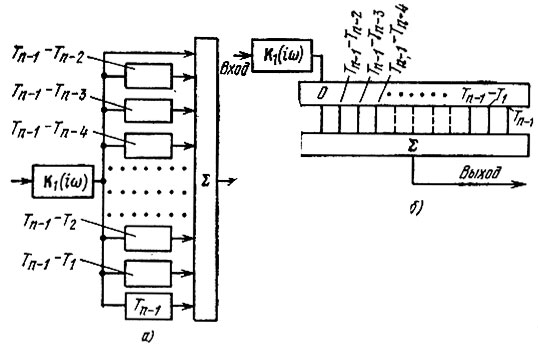
Рис. 12.13. Согласованная фильтрация пачки импульсов (к рис. 12.12)

Максимальный импульс на выходе сумматора получается, когда первый импульс входной последовательности, прошедший через задержку Т_n-1, суммируется со вторым импульсом, прошедшим через задержку Т_n-1 - Т₁, с третьим импульсом, задержанным на Т_n-1 - Т₂, и т. д., вплоть до последнего импульса, проходящего через рассматриваемое устройство без дополнительной задержки. Вместо набора из n линий задержки конструктивно проще и выгоднее применять одну линию задержки с n отводами (рис, 12.13, б). Отводы располагаются таким образом, чтобы соответствующие им задержки нарастали в том же порядке, что и на рис. 12.13, а.

Построение согласованного фильтра значительно упрощается, когда входной сигнал представляет собой последовательность равноотстоящих одинаковых импульсов, т. е. когда

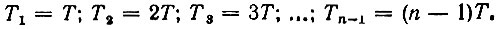
Для этого случая выражение (13.56) можно записать так:

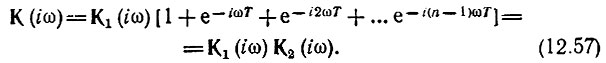
При достаточно большом числе n выражение в квадратных скобках можно свернуть по формуле геометрической прогрессии

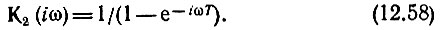
Структура выражения (12.57) указывает на возможность осуществления согласованного фильтра в виде каскадного соединения двух четырехполюсников: одного с передаточной функцией К₁(iω), как и в схеме на рис. 12.13, а согласованного с одиночным импульсом, и другого в виде цепи с обратной связью, содержащей всего лишь одну линию задержки Т (рис. 12.14). Передаточная функция подобной цепи (на рис. 12.14 обведенной штриховой линией) определяется выражением

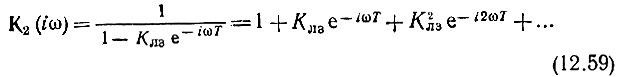
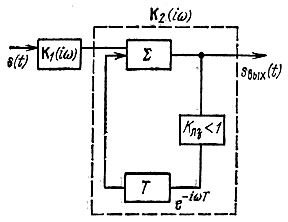
Рис. 12.14. Гребенчатый фильтр

Символом К_лз обозначен безынерционный четырехполюсник, учитывающий затухание в линии задержки (достигающее десятков децибел) и включающий в себя усилитель, компенсирующий это затухание. Для устойчивости цепи коэффициент К_лз должен быть меньше единицы. Сама линия задержки при этом может рассматриваться как идеальная, с передаточной функцией е^-iωT.

При частотах, отвечающих условию ωТ = (2k + 1) π, k = 0, 1, 2, ..., обратная связь отрицательна и К₂(iω) = 1/(1 + К_лз). При частотах ωТ = 2kπ, k = 0, 1, 2, ..., обратная связь положительна и К₂(iω) = 1/(1 - К_лз).

Амплитудно-частотная характеристика цепи приобретает вид, показанный на рис. 12.15. Фильтры с подобной характеристикой называются гребенчатыми. Они эффективны для выделения сигналов в виде периодической последовательности импульсов на фоне белого шума. Чем больше число импульсов в пачке n и чем ближе К_лз к единице, тем лучше приближение цепи к согласованному фильтру.

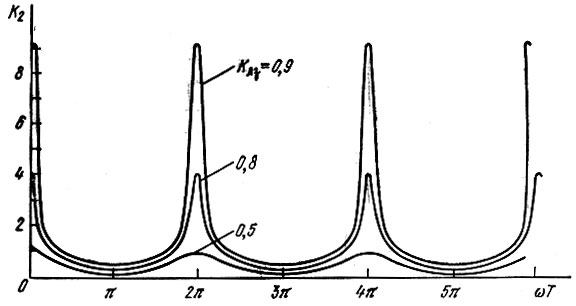
Рис. 12.15. Амплитудно-частотная характеристика гребенчатого фильтра

Импульсная характеристика фильтра К₂(iω) определяется очевидным выражением

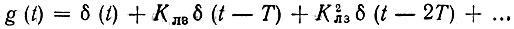
Коэффициенты при единичных импульсах, возникающих на выходе четырехполюсника через интервалы Т, убывают по закону, близкому к экспоненте (при К_лз, близком к единице). Таким образом, импульсная характеристика фильтра К₂ имеет вид, показанный на рис. 12.16 (дельта-функции на рис. 12.16 не обозначены).

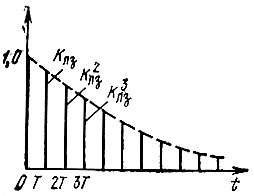
Рис. 12.16. Импульсная характеристика гребенчатого фильтра

Все приведенные выше рассуждения можно распространите и на фильтрацию последовательности радиоимпульсов. Необходимо лишь под К₁(iω) подразумевать коэффициент передачи фильтра, согласованного с одиночным радиоимпульсом из входной последовательности.