12.7. Согласованная фильтрация заданного сигнала при небелом шуме

Пусть на полностью известный сигнал s(t) линейно (аддитивно) накладывается шум с неравномерным энергетическим спектром W(ω) (небелый шум). Требуется синтезировать фильтр, максимизирующий отношение сигнал - помеха. В отличие от ранее рассмотренных задач в данном случае передаточная функция должна быть согласована не только со спектром сигнала S(ω), но также и с энергетическим спектром шума W(ω).

Наиболее простым способом отыскания требуемой передаточной функции К(iω) является приведение заданного шума к белому [1]. Для выяснения сути этого способа рассмотрим вспомогательную структурную схему, показанную на рис. 12.22. На этой схеме К(iω) обозначает искомую передаточную функцию синтезируемого фильтра, а К₁(iω) и 1/К₁(iω) являются передаточными функциями их результирующая передаточная функция равна единице.

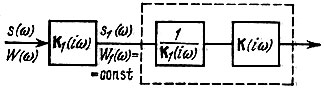
Рис. 12.22. Согласованная фильтрация заданного сигнала при небелом шуме

Так как функцию К₁(iω) можно выбирать произвольно, то модуль этой функции зададим в виде

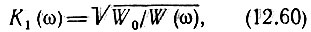
где W₀ - постоянная величина.

Тогда на выходе первого четырехполюсника будет действовать шум с равномерным энергетическим спектром

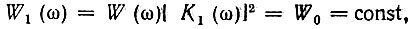
т. е. белый шум.

Само собой разумеется, сигнал на выходе этого четырехполюсника отличается от входного сигнала, так как спектральная плотность

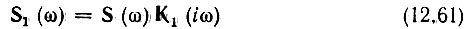
отличается от S(ω). Однако это обстоятельство несущественно; основной задачей является максимизация отношения сигнал-помеха на выходе всего устройства. Поэтому важно отношение энергии сигнала к энергетическому спектру шума, а форма сигнала при этом роли не играет.

Так как в рассматриваемом сечении схемы шум является белым, то для получения на выходе максимума отношения сигнал-помеха вся последующая часть устройства должна иметь передаточную функцию, отвечающую условию (12.16). Таким образом, получаем

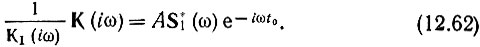
Левая часть этого выражения является результирующей передаточной функцией четырехполюсника, обведенного на рис. 12.22 штриховой линией, а правая часть - функцией комплексно-сопряженной по отношению к спектру S₁(ω) и дополненной множителем e^-iωt₀

Из выражения (12.62) получаем

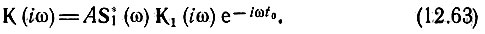
Но из (12.61) следует, что

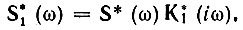
Таким образом,

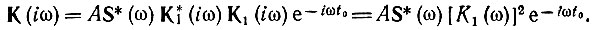
Подставляя сюда соотношение (12.60), окончательно получаем

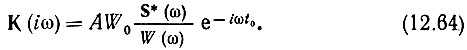
Нетрудно истолковать физический смысл этого соотношения.

Как и в случае белого шума, для максимизации отношения сигнал-помеха в фильтре должна осуществляться компенсация начальных фаз спектра входного сигнала S(ω). Поэтому в правую часть (12.64) входит комплексно-сопряженная функция S*(ω). Однако модуль передаточной функции должен быть, во-первых, пропорционален модулю S(ω) (как и в случае белого шума) и, во-вторых, обратно пропорционален энергетическому спектру шума на входе фильтра. Тем самым обеспечивается подчеркивание тех компонентов спектра сигнала, при которых интенсивность шума меньше.