12.8. Фильтрация сигнала с неизвестной начальной фазой

При обработке сложных сигналов с внутриимпульсной модуляцией начальная фаза θ₀ высокочастотного заполнения в выражении

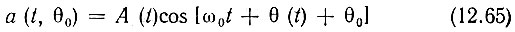
обычно является неизвестной величиной.

Если фильтр согласован с сигналом а(t, 0) = A(t) cos [ω₀t + θ(t)], без учета θ₀, то при наличии фазового сдвига θ₀ фильтр оказывается рассогласованным. Выясним влияние этого рассогласования на выходное колебание.

Основываясь на общем выражении (12.28), представим сигнал на выходе фильтра (сначала при θ₀ = 0) в форме (3.98), (3.99):

Постоянная задержка t₀, входящая в выражение (12.28), для упрощения анализа опущена. Поэтому сдвиг τ заменен t. Кроме того, знак минус в показателе степени заменен плюсом в соответствии со знаком сдвига функции А*(х - t). Как отмечалось в § 3.10, интеграл в последнем выражении имеет смысл корреляционной функции B_А(x) комплексной огибающей A(t).

Введем в рассмотрение начальную фазу θ₀ входного сигнала. Для этого достаточно функцию А(х) домножить на е^iθ₀. Новый интеграл

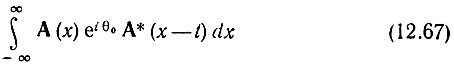
определяет взаимную корреляцию между функциями А(х)е^iθ₀ и А*(х - t), однако после вынесения множителя е^iθ₀ за знак интеграла получается произведение е^iθ₀В_А(t).

Таким образом, приходим к следующему выражению для сигнала на выходе рассогласованного фильтра:

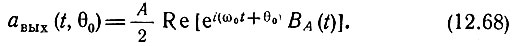
Из сравнения этого выражения с (12.66) вытекает, что для учета начальной фазы достаточно прибавить θ₀ к слагаемому ω₀t, сохранив огибающую выходного сигнала.

Проиллюстрируем этот результат на примере ЛЧМ импульса, рассмотренного в примерах § 3.11 и 12.5.

Из соотношений (3.103) и (3.106'), после замены в них τ на t (задержка сигнала не учитывается), вытекает следующее выражение для корреляционной функции огибающей:

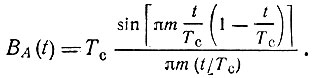
Таким образом,

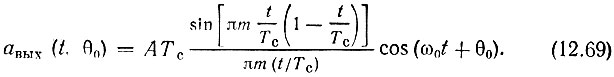
На рис. 12.23 изображено выходное колебание на отрезке времени вблизи пика при θ₀ = 90° для фильтра, согласованного с ЛЧМ сигналом. Параметры входного сигнала соответствуют п.2, § 12.5 (рис. 12.10). В зависимости от величины θ₀ положение пика сжатого сигнала на оси времени может изменяться в пределах ±π/ω₀, т. е. половины периода высокочастотного заполнения. Из этого примера видно, что при достаточно большом числе периодов, приходящемся на длительность сжатого сигнала, влияние θ₀ на величину пика незначительно. Если дальнейшая обработка сигнала ведется по огибающей, то при выполнении указанного выше условия относительно высокочастотного заполнения влияние θ₀ исключается.

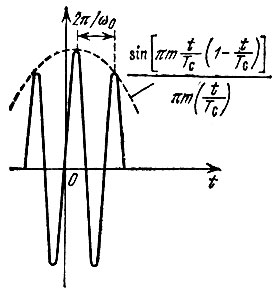
Рис. 12.23. Высокочастотное заполнение сжатого ЛЧМ импульса при начальной фазе сигнала θ₀ = 90°