12.9. Согласованная фильтрация комплексного сигнала

В гл. 3, 6 и др. отмечалось, что комплексная огибающая А(t) узкополосного сигнала a(t) = A(t) cos [ω₀t + θ₀(t) содержит в себе всю информацию, обусловленную как амплитудной, так и угловой модуляцией. Во многих практических задачах радиотехники обработку сигнала целесообразно производить непосредственно по огибающей А(t) с исключением несущей частоты ω₀.

Структурная схема устройства, осуществляющего выделение комплексной огибающей узкополосного сигнала а(t), представлена на рис. 12.24. Устройство состоит из двух одинаковых преобразователей частоты с общим гетеродином, частота которого ω₀ совпадает с несущей частотой сигнала.

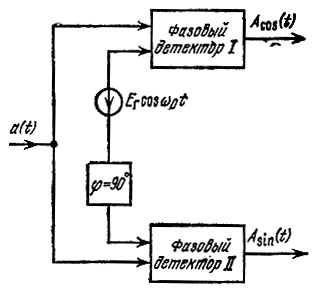
Рис. 12.24. Выделение квадратурных составляющих комплексной огибающей узкополосного колебания

Избирательная цепь на выходе каждого из преобразователей представляет собой фильтр нижних частот (RС-цепь). Полоса прозрачности фильтра предполагается достаточной для неискаженного воспроизведения спектра передаваемого сообщения. При выполнении условия Е_г >> A_макс осуществляется линейное преобразование частоты, в результате которого колебание на выходе первого преобразователя принимает вид [см. формулы (8.74) и (8.77)]

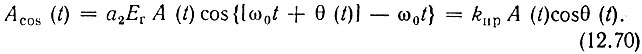
На выходе второго преобразователя, благодаря сдвигу фазы гетеродинного колебания на угол φ = 90°, получается колебание

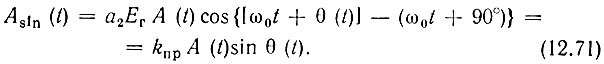
Символом k_пр = а₂Е_г обозначен постоянный коэффициент, имеющий смысл крутизны характеристики преобразования; а₂ - коэффициент при квадратичном члене в выражении (8.10).

Преобразователи, выделяющие на выходе колебание, содержащее информацию о фазе θ(t) (слагаемое ω₀t исключено), обычно называют фазовыми детекторами.

Косинусное A_cos(t) и синусное A_sin(t) колебания совпадают соответственно с действительной и мнимой частями комплексной огибающей А(t) [см. выражение (3.88)]. В этом смысле рассматриваемая обработка является квадратурной.

Совокупность физических колебаний A_cos(t) и A_sin(t), записанная в виде суммы A_cos(t) + iA_sin(t), позволяет трактовать комплексное колебание как физический процесс. Следует при этом иметь в виду, что рассматриваемое комплексное колебание не является аналитическим сигналом. Это объясняется тем, что спектральная плотность комплексной огибающей А(t) не обращается в нуль в области частот ω < 0 (см. п. 3, § 3.10).

Дальнейшую обработку комплексного колебания следует производить по обычным правилам оперирования с комплексными величинами.

Если в результате прохождения узкополосного сигнала

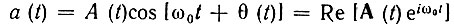
через фильтр с импульсной характеристикой

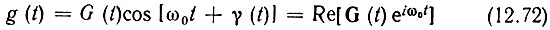
на выходе получается сигнал (см. § 6.6)

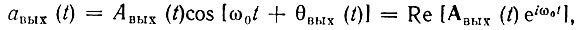
то при эквивалентной квадратурной обработке на выходе фильтра нижних частот сигнал должен иметь вид

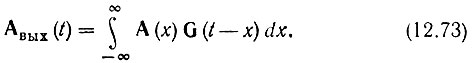
Из этого требования вытекает, что импульсная характеристика искомого фильтра должна совпадать с комплексной функцией G(t). Комплексную импульсную характеристику можно реализовать с помощью двух физических фильтров с вещественными импульсными характеристиками соответственно G_cos(t) = G(t) cos γ(t) и G_sin(t) = G(t) sin γ(t) [см. формулу (12.72)]:

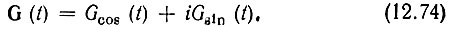
Подставив в (12.73) A(t) по формулам (12.70), (12.71) и G(t) по формуле (12.74), получим

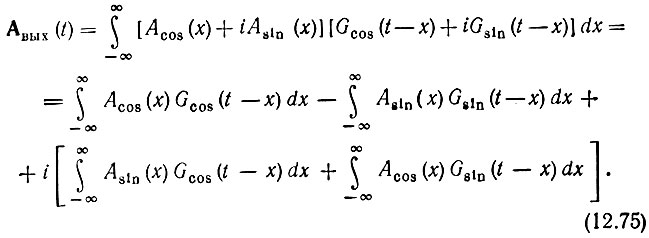
Первый интеграл определяет отклик физического фильтра с импульсной характеристикой (вещественной) G_cos(t) на воздействие A_cos(t), второй интеграл - отклик фильтра с импульсной характеристикой G_sin(t) на воздействие A_sin(t) и т. д.

Алгоритм (12.75) реализуется схемой, представленной на рис. 12.25. Это общий алгоритм, применимый к произвольной функции G(t). В случае же согласованной фильтрации на импульсную характеристику G(t) накладывается условие, вытекающее из требования максимизации пика сигнала. Это условие по аналогии с выражением (12.22) и с учетом (12.66) можно записать в форме

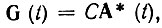
где С - постоянный коэффициент.

Таким образом,

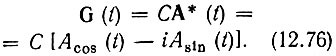
Подстановка этого выражения в (12.75) приводит к следующему результату:

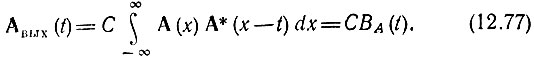
Из этого выражения следует, что при строго согласованной фильтрации сигнал на выходе рассматриваемого устройства является вещественной функцией, совпадающей по форме с корреляционной функцией комплексной огибающей входного колебания.

Введем в рассмотрение неизвестную начальную фазу θ₀. Для этого входящие в выражение (12.75) функции A_cos(х) и A_sin(х) должны быть домножены на е^iθ₀, в результате чего получится

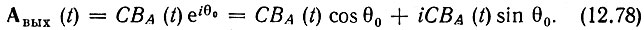
При θ₀ ≠ 0 суммарное колебание на выходе сумматоров I и II является комплексным. На рис. 12.26 воспроизведена схема, показанная на рис. 12.25 (слева от штриховой линии) с измененными знаками выходов косинусного и синусного фильтров. Импульсные характеристики указанных фильтров сохранены прежними. Справа от штриховой линии показаны дополнительные устройства, необходимые для исключения неизвестной начальной фазы: квадрирующие устройства (КУ), сумматор и устройство для извлечения квадратного корня из суммы квадратов. В результате этой дополнительной обработки получается колебание СВ_А(t), совпадающее с (12.77), Продолжая пример с согласованной фильтрацией ЛЧМ импульса, приведенный в предыдущем параграфе, получаем

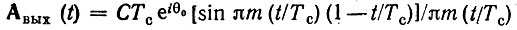
а при полной обработке по схеме, изображенной рис. 12.26:

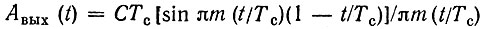
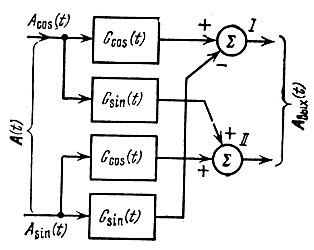
Рис. 12.25. Комплексный фильтр

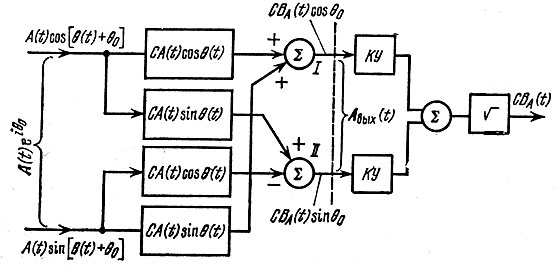
Рис. 12.26. Комплексный фильтр, согласованный с комплексной огибающей узкополосного колебания и дополнительный элементами квадратурной обработки

Возведение в квадрат и извлечение корня являются нелинейными преобразованиями сигнала. Однако эта часть обработки производится после максимизации отношения сигнал - помеха в линейном согласованном фильтре, поэтому эффект взаимодействия сигнала и помехи менее вреден, чем при непосредственном воздействии сигнала и помехи на нелинейное устройство.