13.2. Алгоритм дискретной свертки (во временной области)

Схема устройства дискретной обработки континуального сигнала (без цифрового кодирования) представлена на рис. 13.2.

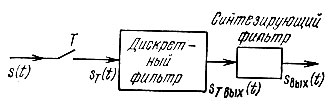
Рис. 13.2. Схема дискретной обработки сигнала

Процедуру дискретизации входного сигнала (взятие выборок) удобно рассматривать как умножение функции s(t) на периодическую последовательность y_T(t) тактовых импульсов. В качестве таких импульсов обычно рассматривают дельта-функции, так что функцию y_T(t) можно определить выражением

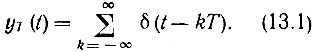
График этой функции показан на рис. 13.3, б (цифра единица обозначает площадь тактового импульса).

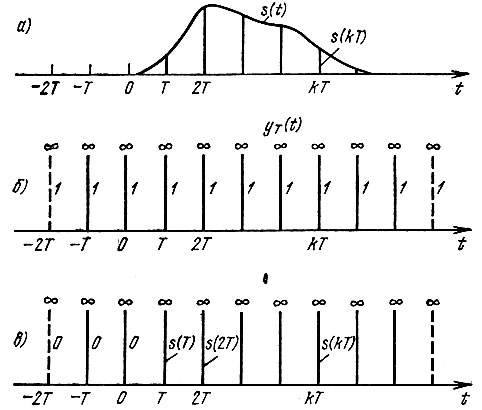
Рис. 13.3. Дискретизация сигнала: а - исходный континуальный сигнал; б - последовательность тактовых импульсов; в - дискретные отсчеты сигнала

Тогда дискретизированный сигнал

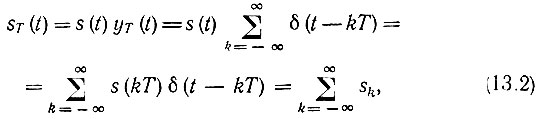
где

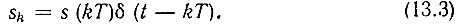
При таком обозначении s_k имеет смысл бесконечно короткого импульса, расположенного на оси времени в точке t = kT и обладающего площадью, численно равной выборке s(kT). Таким образом, выборки s(kT) из сигнала s(t) (рис. 13.3, а), являются весовыми коэффициентами дельта-функции (рис. 13.3, в)^*.

^* (Следует иметь в виду, что по своей размерности s_T(t) отличается от s(t), поскольку функция δ(t) имеет размерность 1/t. Для сохранения размерности выражение (13.3) следовало бы записать в форме s_k = T_s(kT)×δ(t - kT), что равносильно приравнению площади импульса s_k площади прямоугольного импульса с основанием Т и амплитудой s(kТ) [4]. )

Дискретизированный сигнал S_T(t) подается на дискретный фильтр, влияние которого на S_T(t) должно быть эквивалентно влиянию некоторого аналогового фильтра на s(t). Пусть импульсная характеристика последнего g(t) задана. Тогда сигнал на выходе аналогового фильтра определяется сверткой (см. выражение (6.12)]:

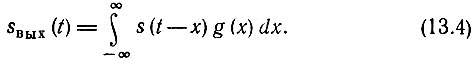
Дискретный эквивалент свертки при надлежащем выборе шага Т можно записать в форме

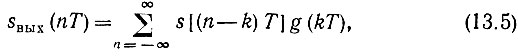
где s_вых(nТ) - n-я выборка из s_вых(t), а соответствующий этой выборке импульс согласно (13.3)

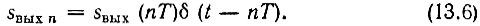
В выражении (13.5) g(kT) имеет смысл k-й выборки из импульсной характеристики аналогового фильтра, показанной на рис. 13.4 штриховой линией.

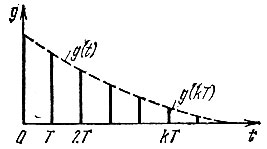
Рис. 13.4. Дискретизация импульсной характеристики аналогового фильтра

Выражение (13.5) можно рассматривать как алгоритм дискретной обработки, эквивалентной пропусканию сигнала через аналоговый фильтр с заданной импульсной характеристикой g(t).

При отсчете времени от начала входного сигнала выражение (13.5) принимает вид

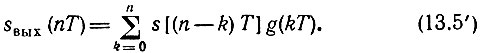
Верхний предел суммирования следует из условия, что при k > n s[(n - k)T] = 0, а нижний - из условия, что при t < 0 g(t) = 0.

Схема устройства, обладающего требуемой дискретной импульсной характеристикой g_T(t), представлена на рис. 13.5, На этой схеме буквами а₀, а₁, а₂, ..., а_Н обозначены не зависящие от частоты коэффициенты усиления, а T - идеальная линия задержки; задержка совпадает с темпом поступления выборок сигнала s(t). Подбором коэффициентов а₀ = g(0), а₁ = g(T), а₂ = g(2T), ... можно, в принципе, осуществить весьма сложные импульсные характеристики g_T(t).

Очевидно, что импульсная характеристика рассматриваемого устройства должна записываться в форме

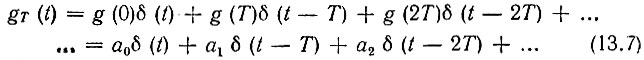
Таким образом, a_k = g(kT) является лишь весовым коэффициентом при дельта-функции δ(t - kT). При подаче на вход схемы, обведенной на рис. 13.5 штриховой линией, дискретного сигнала s_T(t) на выходе сумматора ∑ получается дискретная последовательность импульсов s_{T вых}(t), а на выходе синтезирующего фильтра - профильтрованный непрерывный сигнал s_вых(t).

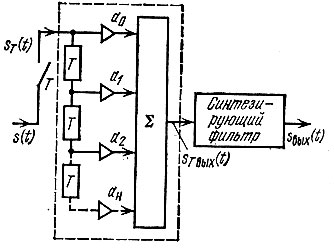
Рис. 13.5. Дискретный фильтр

Осуществить дискретный фильтр непосредственно по схеме на рис. 13.5 можно лишь для относительно простых сигналов, обладающих небольшой базой N = 2f_mT_c. (Т_с = NT - длительность обрабатываемой реализации сигнала.) Однако алгоритм (13.5) широко используется при моделировании фильтров с помощью ЭВМ.

Основная трудность реализации дискретного фильтра заключается также в осуществлении элемента памяти Т. Эта трудность отпадает при переходе к цифровой фильтрации, когда запоминание сигнала на любое необходимое время осуществляется с помощью двоичных элементов (триггеров). Важным параметром дискретного фильтра является память Т. Этот параметр оказывает решающее влияние на основные характеристики фильтра - передаточную функцию и импульсную характеристику.