13.3. Дискретные преобразования Фурье

Для уяснения особенностей дискретной фильтрации важное значение имеет выявление структуры спектра дискретизированного сигнала s_T(t).

Пусть заданы спектральная плотность S(ω) исходного сигнала s(t) (континуального) и шаг взятия выборок Т. Рассматривая s_T(t) как произведение s(t) y_T(t), где y_T(t) определяется выражением (13.1), находим спектральную плотность функции s_T(t) по формуле

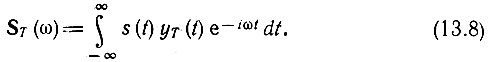
Периодическую последовательность дельта-импульсов можно представить в виде ряда Фурье

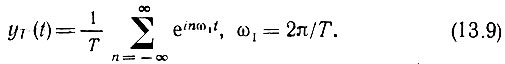
Коэффициенты этого ряда равны 1/T поскольку спектральная плотность одиночного дельта-импульса равна единице, а период повторения импульсов равен Т [см. формулу (2.55)].

Подставив (13.9) в (13.8), получим

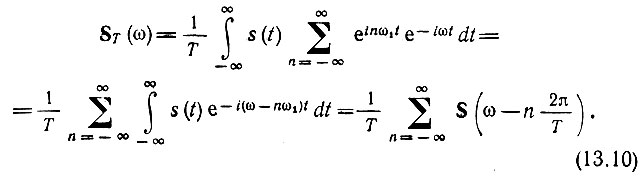
Итак, спектр S_T(ω) дискретизированного сигнала представляет собой последовательность спектров^*S(ω) исходного сигнала s(t), сдвинутых один относительно другого на величину 2π/Т.

^* (По своей размерности величина S_Т(ω) отличается от S(ω) так же, как и сами оригиналы s_T(t) и s(t) (см. сноску ранее).)

Если шаг взятия выборок отвечает условию Т < 1/2f_m (по теореме отсчетов) и, следовательно, ω_m ≤ π/Т, го отдельные спектры не перекрываются, как это показано на рис. 13.6, и могут быть разделены с помощью фильтров на выходе устройства.

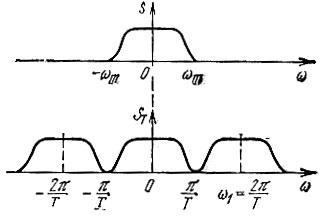
Рис. 13.6. Спектр дискретизированного сигнала

Спектр дискретизированного сигнала приобретает периодическую форму. Выражение (13.10) полезно для установления связи между S(ω) и S_T(ω), однако в общем случае, при произвольном соотношении между Т и S(ω), когда возможно перекрытие спектров, применение формулы (13.10) становится затруднительным. Кроме того, желательно иметь формулу, позволяющую находить S_T(ω) непосредственно по заданным временным выборкам s(kT), без обращения к спектру S(ω) исходного континуального сигнала. Такую формулу легко получить, если преобразование Фурье применить к выражению (13.2). При отсчете времени от первой выборки s(0) получим

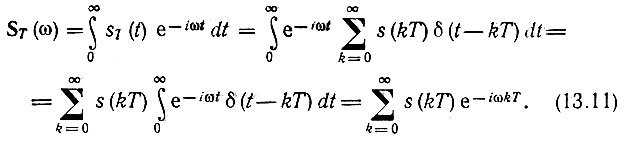
Реальный сигнал аппроксимируется с помощью конечного числа отсчетов. При числе отсчетов N выражение (13.11) принимает вид

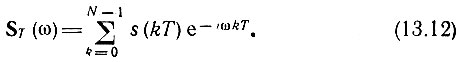
При использовании ЭВМ требуется дискретизация сигнала как во временной, так и в частотной области. В последнем случае частотный спектр S_T(ω) определяется совокупностью своих значений S_T(nω₁) на дискретных частотах ω = nω₁.

В § 2.15 было установлено, что число степеней свободы сигнала одинаково как по времени, так и по частоте. Частотный интервал сох между соседними отсчетами должен быть приравнен ω₁ = 2ω_m/N.

Так как ω_m = π/Т, то ω₁ = 2π/NT. Это соотношение согласуется с определением Δω = 2π/Т_с в § 2.15, поскольку произведение NT имеет смысл длительности Т_с исходного (континуального) сигнала.

Подставив в выражение (13.12) ω = nω₁, получим формулу для определения частотных выборок

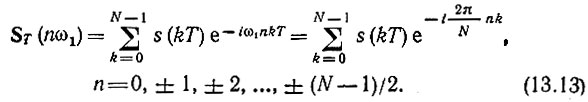
Соотношение (13.13) называется дискретным преобразованием Фурье (ДПФ).

При увеличении |n| свыше (N - 1)/2 функция S_T(nω₁) повторяется периодически. Поэтому S_T(-ω₁) можно приравнять S_T[(N - 1)ω₁], соответственно S_T(-2ω₁) = S_T[(N - 2)ω₁] и т. д. Это позволяет записать выражение (13.13) в несколько измененной форме, удобной для вычисления на ЭВМ:

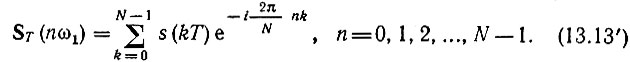
Нумерация отсчетов при нечетном и четном значениях N поясняется рис. 13.7, 13.8 при N = 7 и 8. Функция s(t) в этих примерах предполагается вещественной, поэтому частотные выборки, расположенные симметрично относительно точки n = 0 (ω = 0), должны образовывать комплексно-сопряженные пары. Для выполнения этого условия выборки S_T(nω₁) должны располагаться в середине соответствующих частотных интервалов (на рис. 13.7, 13.8 заштрихованных). В нижних частях этих рисунков в скобках обозначены номера отсчетов, соответствующих отрицательным значениям n, после сдвига отсчетов вправо на N частотных интервалов. Как при четном, так и нечетном N полная ширина спектра 2ω_m = Nω₁.

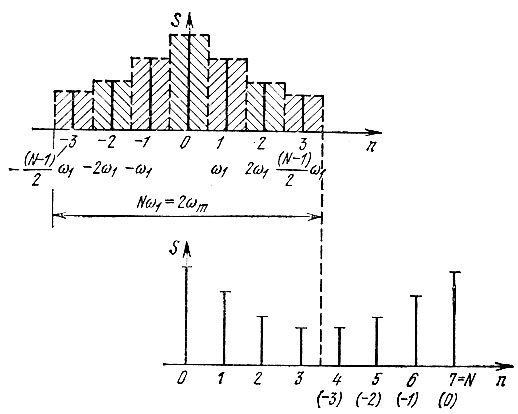
Рис. 13.7. Дискретное преобразование Фурье. Нумерация отсчетов при нечетном N

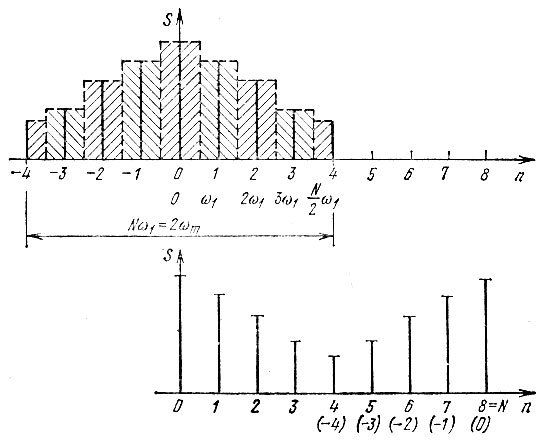
Рис. 13.8. Нумерация отсчетов при четном N

Можно ввести и понятие обратного дискретного преобразования Фурье. По аналогии с парой преобразований Фурье (2.48), (2.49) дискретное обратное преобразование можно определить как

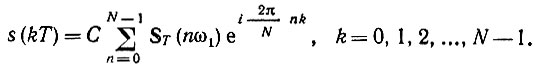
Для определения постоянного коэффициента С подставим в это выражение S_T(nω₁) из (13.13'):

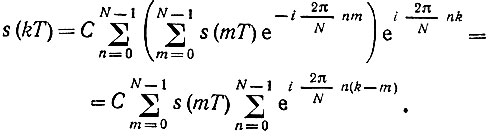
При m = k внутренняя сумма обращается в N, а при любом другом значении m - в нуль (как сумма векторов, концы которых делят окружность единичного радиуса на равные дуги). Следовательно, в правой части остается одно слагаемое С s(kT)N, из чего вытекает равенство С = 1/N. Таким образом, обратное дискретное преобразование Фурье, принимает следующую форму:

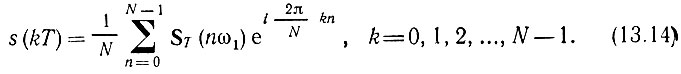
Как и при прямом ДПФ, вне интервала 0 ≤ k ≤ N - 1 функция s(kT) продолжается периодически.

Некоторые из свойств непрерывных преобразований Фурье, рассмотренных в § 2.7, нетрудно сформулировать также и для ДПФ.

1. Линейность преобразования: спектр суммы (разности), дискретных сигналов равен сумме (разности) их спектров.

2. Сдвиг дискретного сигнала во времени. Повторяя рассуждения, приведшие к выражению (2.57), нетрудно показать, что если сигналу s(t), представленному совокупностью отсчетов s(kT), k = 0, 1, 2, ..., N - 1, соответствует ДПФ S_T(nω₁), то сигналу s(t + mТ), где m - целое число, соответствует ДПФ 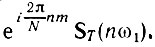Иными словами, сдвиг последовательности отсчетов на m интервалов приводит лишь к изменению фазочастотной характеристики ДПФ на величину ^2π/_N nm (теорема запаздывания).

3. Теорема свертки. Если ДПФ S_T(nω₁) соответствует дискретному сигналу 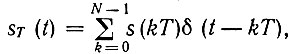а ДПФ G_T(nω₁) - сигналу 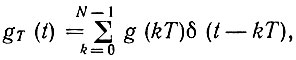то произведению S_T(nω₁) G_T(nω₁) соответствует сигнал

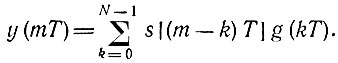
Вывод этого выражения аналогичен выводу (2.64) [см. также (13.7)].

В предыдущих главах отмечалось, что ограничение сигнала одновременно по длительности и по ширине спектра неосуществимо. Представление сигнала конечным числом импульсов N и конечным числом частотных выборок N неизбежно сопровождается некоторыми искажениями формы сигнала. Однако эти искажения проявляются не при переходе от s(kT) к S_T(nω₁) или при обратном переходе от S_T(nω₁) к s(kT) с помощью преобразований (13.13), (13.14), а при переходе от дискретного представления к континуальному. Этот вопрос рассматривается в следующем параграфе.