13.4. Погрешность дискретизации сигналов конечной длительности

В § 2.14 отмечалась противоречивость требования ограничить сигнал одновременно по длительности и по спектру. Это противоречие проявляется особенно существенно при дискретизации относительно коротких импульсных сигналов.

Пусть задан сигнал s(t) длительностью Т_с и, строго говоря, с бесконечно широким спектром S(ω). При выборе шага дискретизации Т на основании теоремы Котельникова (см. § 2.14) возникает неопределенность в оценке величины ω_m - граничной частоты спектра сигнала. Выбор этой частоты определяет шаг Т = π/ω_m, а при заданной длительности сигнала T_c число дискретных отсчетов N = Т_c/Т = Т_сω_m/π.

Для восстановления сигнала в континуальной форме требуется фильтр с полосой прозрачности |ω| = ω_m (см. § 13.3). Для упрощения анализа исходим из идеального фильтра с АЧХ

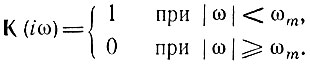
Фазочастотная характеристика подобного фильтра в полосе прозрачности линейна и вносит лишь задержку сигнала, которую дальше учитывать не будем.

Фильтр с указанной выше полосой пропускания подавляет составляющие спектра S(ω) с частотами ω, превышающими ω_m. Поэтому под ошибкой, погрешностью дискретизации можно подразумевать функцию времени, соответствующую отсекаемой части спектра. Обозначим эту функцию Δs(t). Тогда

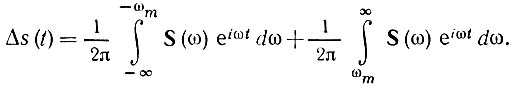
Проиллюстрируем это выражение на примере простого сигнала в виде импульса прямоугольной формы (рис. 13.9, а).

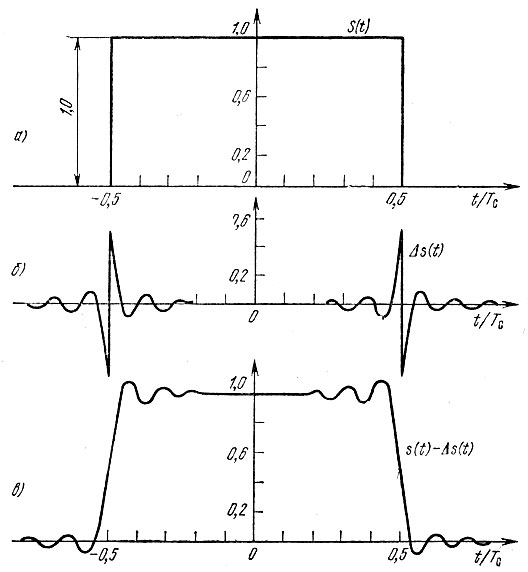
Рис. 13.9. Искажение формы импульса при усечении его спектра граничной частотой 2f_mT_c = 16: а - исходный импульс; б - напряжение ошибки; в - искаженный импульс

Спектральная плотность этого сигнала s(t), равная [см. (2.68)]

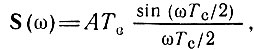
является четной функцией ω. Поэтому выражение для Δs(t) легко привести к виду

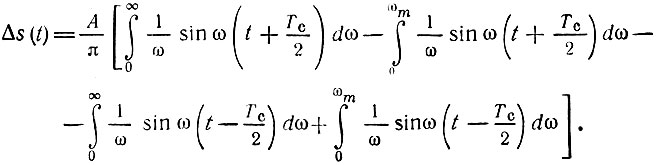
Учитывая известные соотношения

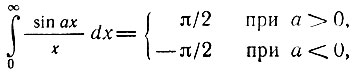
приходим к следующему результату:

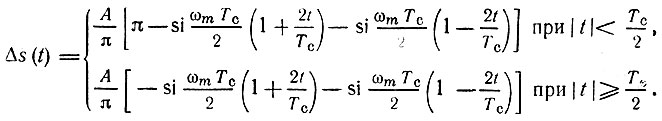
В этих выражениях 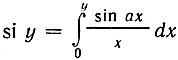- интегральный синус. Пусть для дискретизации импульса отводится N отсчетов. Тогда 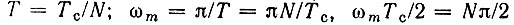и предыдущее выражение записывается в форме

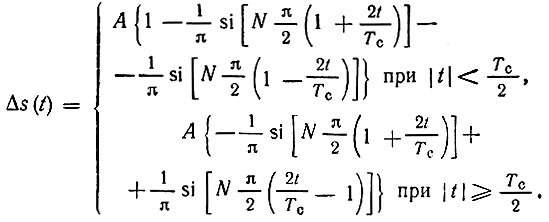
Графики функции Δs(t) и сигнала на выходе фильтра при А = 1 представлены на рис. 13.9, б и в. Любопытно, что для прямоугольного импульса характер функции Δs(t) определяется лишь параметром N = 2f_mT_c.

К определению функции Δs(t) можно также подойти, рассматривая воздействие на синтезирующий фильтр последовательности физических импульсов, соответствующих выборкам из сигнала s(t). Отклик фильтра на выборку s(nТ) равен s(nT) g(t - nТ), где g(t) - импульсная характеристика, определяемая выражением [при К(iω) = 1, |ω| ≤ ω_m]

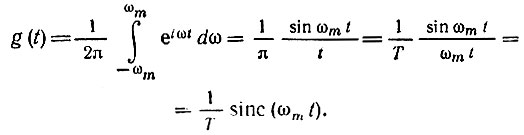
Функция sinc(ω_mt) является базисной функцией ряда Котельникова (см. § 2.15). Следовательно, функцию Δs(t), существующую после окончания сигнала s(t), можно найти суммированием функций s(nT) g(t - nТ) от всех выборок, предшествующих моменту t = Т_с/2. В дискретных точках t = kT функция Δs(t) равна нулю, поскольку все слагаемые в указанных точках равны нулю. Из этого следует, что увеличение интервалов Т приводит к искажению сигнала лишь между отсчетными точками. Нетрудно показать, что протяженность функции Δs(t) практически составляет 3-4 такта. Следовательно, с увеличением числа отсчетов N доля указанного отрезка времени от общей длительности импульса уменьшается.