13.5. Дискретные преобразования Лапласа

Переходя в выражении (13.11) к новой переменной р = σ + iω, можно, как и в § 2.13, ввести понятие дискретного преобразования Лапласа:

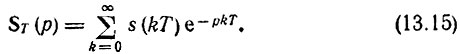
Определение оригинала, т. е. функции s_T(t), по заданному изображению S_T(р) можно осуществить с помощью обратного дискретного преобразования Лапласа, которое записывается в обычной форме

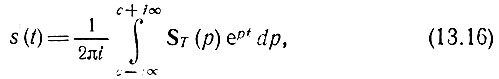
совпадающей с (2.107).

Покажем, что подстановка в (13.16) S_T(р) по формуле (13.15) приводит к требуемому результату:

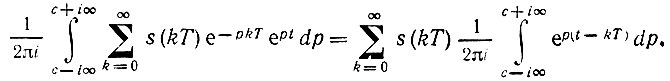
Учитывая (см. также табл. 2.1), что при с → 0

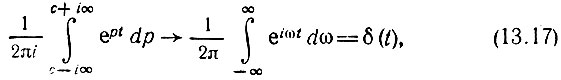
правую часть предыдущего выражения нетрудно привести к виду

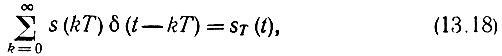
совпадающему с (13.2). Таким образом, убеждаемся, что выражение (13.16) определяет всю последовательность выборок сигнала s(t).

Для определения одной n-й выборки s(nТ), без множителя δ(t - nТ), можно применять более простое выражение

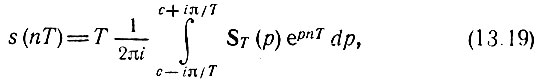
в котором интегрирование ведется в пределах одного частотного интервала от -π/Т до π/T.

Действительно, подставив в (13.19), как и ранее, S_T(р) по формуле (13.15), получим

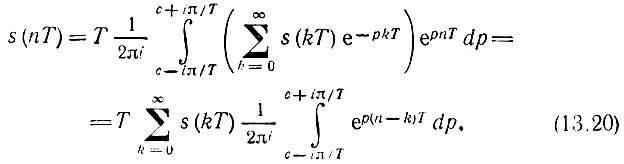
Вычислим интеграл

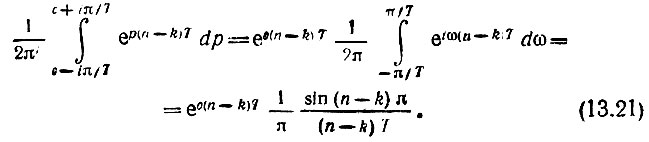
При n = k это выражение равно 1/T, а при n ≠ k - нулю. Следовательно, в правой части (13.20) остается одно слагаемое s(nТ) = s(кТ).

В тех случаях, когда дискретная последовательность s_T(t) не равна нулю при отрицательных индексах k, приходится применять двустороннее дискретное преобразование Лапласа.

По аналогии с выражениями (2.108), (2.112) и (2.114) представим его в форме

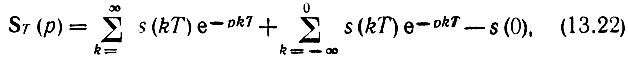
где s(0) компенсирует учет индекса k = 0 в обеих суммах.

Положив во второй сумме k = -m, получим

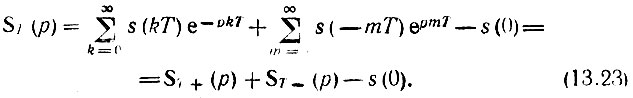
В частном случае, при четной функции s(t), когда s(-mT) = s(mТ), имеет место соотношение, аналогичное (2.116):

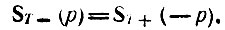
Тогда

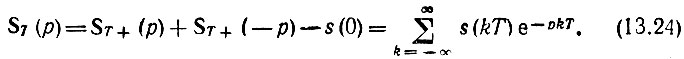
В выражениях (13.23), (13.24) S_T+ - одностороннее преобразование, определяемое выражением (13.15).

Нетрудно определить область сходимости ряда (13.23). Эта область представляет собой полосу ограниченную значениям σ₁ и σ₂ (см. §2.13, рис. 2.33). Последние определяются свойствами непрерывного сигнала, из которого получены дискретные последовательности при t > 0 и t < 0.