13.6. Передаточная функция дискретного фильтра

Вернемся к схеме на рис. 13.2 и составим выражение для передаточной функции дискретного фильтра в виде отношения

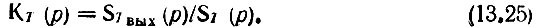
Здесь S_T(р) и S_{T вых}(р) - рассмотренные в предыдущем параграфе изображения по Лапласу соответственно для дискретных входного и выходного колебаний.

Первая из этих функций определяется односторонним преобразованием Лапласа (13.15). Для составления аналогичного выражения S_{T вых}(р) необходимо задать алгоритм работы счетного устройства. Рассмотрим сначала более простой фильтр, в котором не используется обратная связь. В соответствии с выражениями (13.5'), (13.6), а также со схемой на рис. 13.5 импульс S_{вых n} на выходе в момент t = nТ

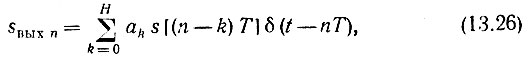
где Н - число запоминаемых и фактически суммируемых предшествующих импульсов входной последовательности (т. е. число элементов памяти Т на рис. 13.5).

Полная последовательность выходных импульсов

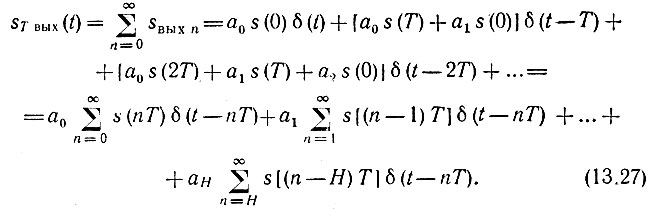
Первая сумма в правой части этого выражения (с коэффициентом а₀) есть входная импульсная последовательность (13.2), вторая - та же последовательность, задержанная на время T, третья - на 2Т и т. д. Следовательно, преобразование Лапласа от выражения (13.27) будет

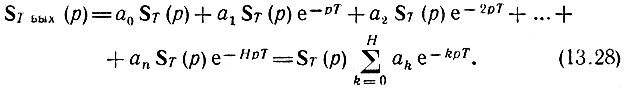
Разделив выражение (13.28) на S_T(р) и учитывая (13.25), получим

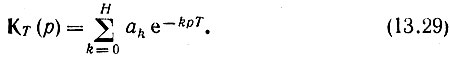
Приравнивая р = iω, находим передаточную функцию как функцию частоты ω:

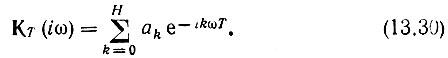
Выражения (13.29), (13.30) вытекают и непосредственно из эквивалентной схемы, представленной на рис. 13.5. При этом предполагается, что коэффициент передачи сумматора ∑ равен единице.

Подбором постоянных а₀, а₁, ..., а_Н можно синтезировать фильтры с различными амплитудно-частотными и фазочастотными характеристиками.

Нетрудно убедиться в периодичности функции К_T(iω). Действительно, добавив к аргументу ω величину n2π/T, где n - любое целое число, и учтя, что e^-ikn2π = 1, получим

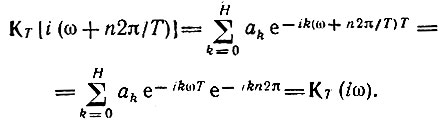
Передаточную функцию дискретного фильтра можно записать в форме^*

^* (Выражение (13.31) можно получить, применив преобразование Фурье к импульсной характеристике дискретного фильтра. Последнюю нужно представить в виде выражения

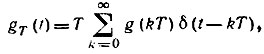
которое отличается от (13.7) множителем T, необходимым для вocстaнoвлeния требуемой размерности и нормирования (см. сноску выше).)

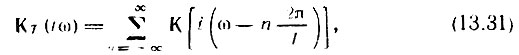
где К(iω) - передаточная функция того же фильтра в отсутствие дискретизации входного сигнала. Выражение (13.31) аналогично выражению (13.10).

Таким образом, передаточная функция дискретного фильтра имеет периодическую структуру, так же как и спектры входного S_T(iω) и выходного S_{T вых}(iω) сигналов. Это положение иллюстрируется рис. 13.10 для фильтра нижних частот, на вход которого подается гармоническое колебание s(t) = А₀ cos ω₀t со спектральной плотностью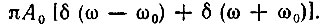

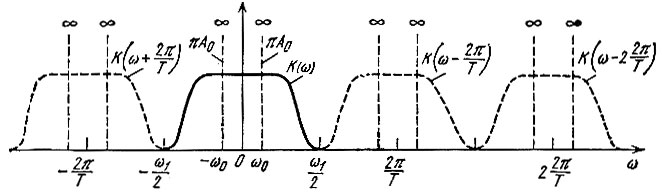
Рис. 13.10. Амплитудно-частотная характеристика дискретного фильтра

Сплошной линией показана амплитудно-частотная характеристика фильтра в центральном интервале (-ω₁/2, ω₁/2). После преобразования дискретного сигнала в непрерывный (с помощью синтезирующего фильтра, изображенного на рис. 13.1) только этот частотный интервал и определяет спектральный состав выходного сигнала.

По передаточной функции К_T(р) можно найти изображение по Лапласу S_{T вых}(р) = S_T(р) К_T(р), а затем с помощью обратного преобразования Лапласа и выходной (дискретный) сигнал

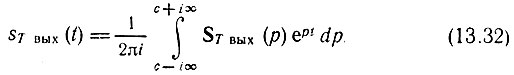
Поясним применение приведенных выше соотношений для простейшего фильтра первого порядка, изображенного на рис. 13.11, а. Импульсная характеристика подобного фильтра представляет собой пару импульсов [см. выражение (13.7)]

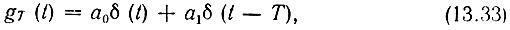
а алгоритм вычислительного устройства в соответствии с выражением (13.26)

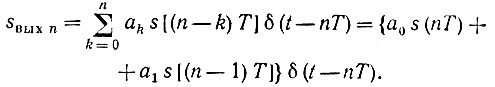
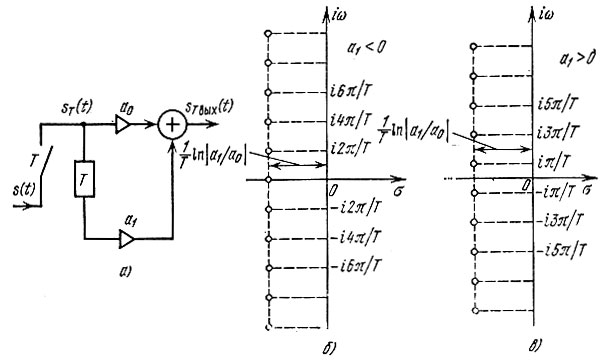
Рис. 13.11. Дискретный фильтр первого порядка (а) и положение нулей передаточной функции на p-плоскости при а₁ < 0 и а₁ > 0 (в)

Указанному алгоритму соответствует передаточная функция

[Этот результат можно получить и непосредственно из выражения (13.29).]

Нули передаточной функции на p-плоскости определяются как корни уравнения 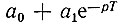или

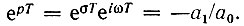
Обозначив корни выражением p_0m = σ_0m + iω_0m, получим 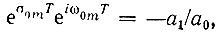откуда вытекают равенства

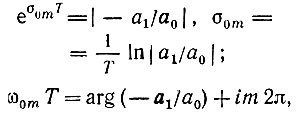
где m - любое целое число.

Коэффициенты а₀ и а₁ - вещественные числа, причем условимся считать а₀ > 0. Тогда при а₁ < 0 arg (-а₁/а₀) = 0 и ω_0m = m2π/T. При а₁ > 0 arg (-а₁/а₀) = π и ω_0m = (2m + 1) π/Т.

Указанные значения ω_0m совместно с σ_0m и определяют положение нулей передаточной функции при а₁ < 0 и при а₁ > 0 (рис 13.1).

Из выражения

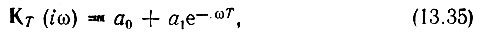
получаемого заменой в (13.34) р на iω, нетрудно вывести формулу для амплитудно-частотной характеристики

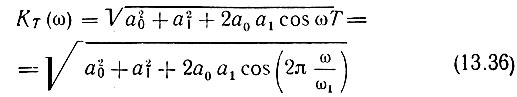
и для фазочастотной характеристики

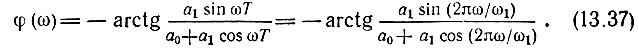
В этих выражениях ω = 2π/Т = 2πf₁ - угловая частота повторения импульсов при дискретизации сигнала.

Амплитудно-частотные характеристики при нескольких значениях ах представлены на рис. 13.12. Вне частотного интервала 0, ω₁ характеристики должны быть продолжены периодически. Из рис. 13.12 видно, что при а₁ = -1 и а₀ = 1 фильтр можно использовать для подавления колебаний с частотами ω = 0, ω = ω₁, ω = 2ω₁, ..., а при а₁ = 1 для подавления частот 0,5ω₁; 1,5ω₁, 2,5ω₁, ...

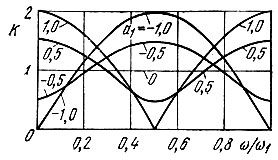
Рис. 13.12. Амплитудно-частотная характеристика цифрового фильтра первого порядка (см. рис. 13.11, а)

Подобные фильтры часто называют гребенчатыми режекторными фильтрами.