13.7. Передаточная функция рекурсивного фильтра

Возможности фильтра значительно расширяются при введении в схему, представленную на рис. 13.5, цепей обратной связи (см. рис. 13.13). (Далее будет показано, как такую схему можно упростить, используя элементы памяти Т одновременно для прямых и обратных связей.) Значение сигнала на выходе сумматора в любой момент времени nТ зависит не только от Н выборок входного сигнала, но и от некоторого количества выборок выходного сигнала в предшествующие моменты. Подобные фильтры называются рекурсивными. Для рекурсивного фильтра выражение (13.26) следует заменить более общим выражением

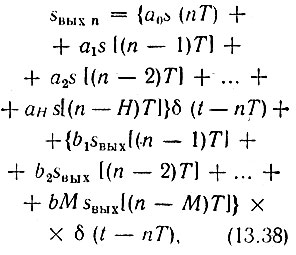
где М - число суммируемых предшествующих выходных импульсов.

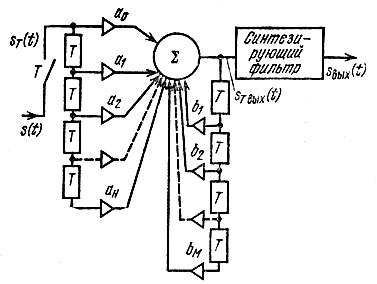
Рис. 13.13. Цифровой фильтр с обратными связями

По аналогии с (13.27), (13.28) легко получить изображение по Лапласу для всей последовательности выходных импульсов

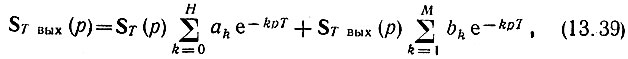
откуда

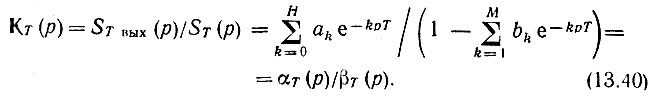
Полученную функцию можно трактовать как передаточную функцию каскадного соединения двух фильтров: одного с передаточной функцией 1/β_T(р), второго - с передаточной функцией α_T(р). Такому представлению отвечает каноническая схема, показанная на рис. 13.14. Число элементов памяти Т в этой схеме вдвое меньше, чем в схеме на рис. 13.13.

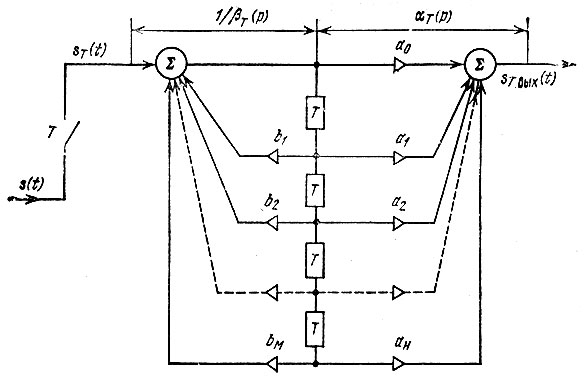
Рис. 13.14. Каноническая схема цифрового рекурсивного фильтра

Рекурсивные фильтры позволяют получить частотные характеристики, присущие фильтрам, передаточные функции которых на плоскости р = σ + iω имеют не только нули (как схема рис. 13.2), но и полюса.

Поясним выражение (13.39) на примере простейшего фильтра, в котором запоминается всего лишь один предшествующий импульс. Алгоритм подобного фильтра [см. (13.38)] принимает вид

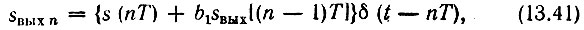
а схема его изображена на рис. 13.15.

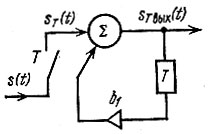
Рис. 13.15. Рекурсивный фильтр первого порядка

Передаточная функция рассматриваемого фильтра по формуле (13.40)

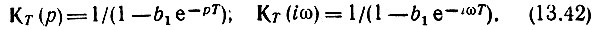
Полюса передаточной функции расположены в точках

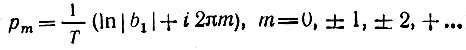
(рис. 13.16, а, б).

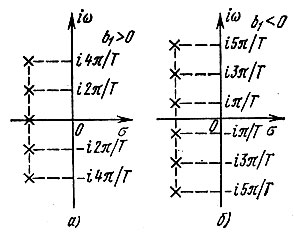
Рис. 13.16. Расположение полюсов передаточной функции рекурсивного фильтра

При любом знаке b₁ для устойчивости цепи должно выполняться условие |b₁| < 1. Изложенные в гл. 5 критерии устойчивости непрерывных линейных цепей с обратной связью с непринципиальными изменениями применимы и к дискретным системам.

Амплитудно-частотная (рис. 13.17) и фазочастотная характеристики рассматриваемой цепи

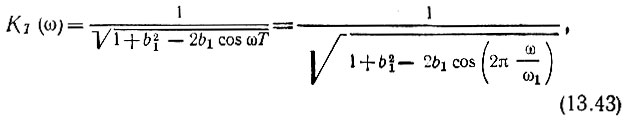
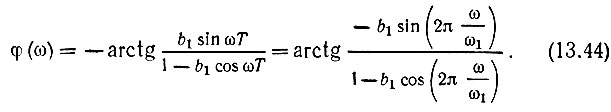
Амплитудно-частотная характеристика при нескольких значениях b₁ представлена на рис. 13.17.

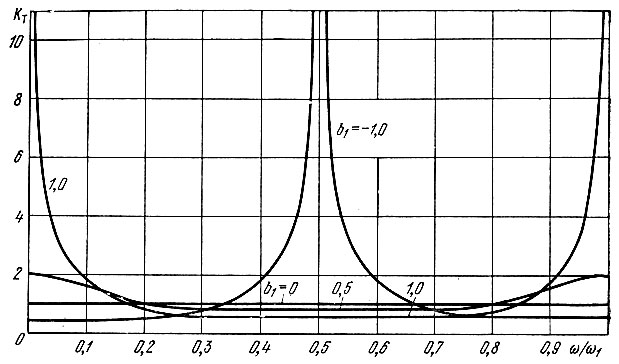
Рис. 13.17. Амплитудно-частотные характеристики рекурсивного фильтра (см. рис. 13.15)

Схема на рис. 13.15 соответствует гребенчатому фильтру, выделяющему колебания с частотами ω = 0, ω₁, 2ω₁, ... при коэффициенте b₁, близком к единице, и с частотами ω = 0,5ω₁, 1,5ω₁, 2,5ω₁, при b₁, близком к -1 (в обоих случаях |b₁| < 1).

Использование передаточной функции в форме (13.40) для анализа дискретных цепей более высокого порядка оказывается затруднительным. Существенное упрощение анализа можно достичь, применяя метод z-преобразования.