13.9. Z-преобразование временных функций

Основываясь на приведенных в § 13.5 дискретных преобразованиях Лапласа, составим аналогичные выражения для z-преобразований, подставляя е^рТ = z.

Выражение (13.15) принимает вид

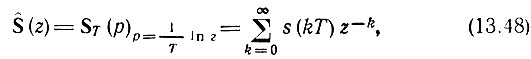
называемое прямым z-преобразованием.

Найдем функцию Sˆ(z) для некоторых простых временных функций s_T(t).

1. Последовательность выборок из сигнала s(t) = 1, t ≥ 0. В этом случае s(kТ) = 1, k = 0, 1, 2, ..., ∞, и в соответствии с (13.48)

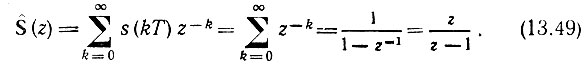
Нуль z₀ = 0, полюс z_п = 1.

2. Последовательность выборок из сигнала 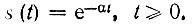В этом случае 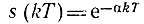и

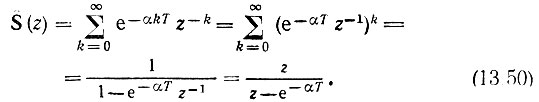
Нуль z₀ = 0, полюс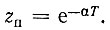

3. Последовательность выборок из сигнала s(t) = a^αt, t ≥ 0, a < 1. В этом случае s(kT) = e^-αkT и

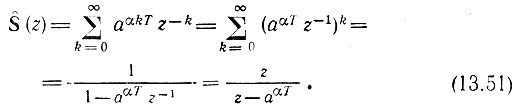
Нуль z₀ = 0, полюс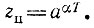

4. Последовательность выборок из сигнала s(t) = cos ω₀ T, t ≥ 0. В этом случае 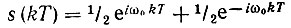и

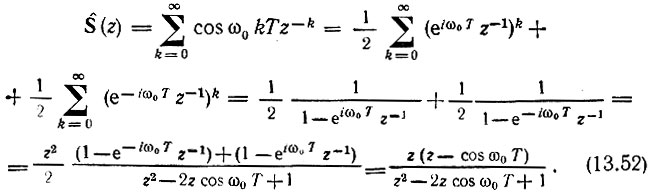
Нули: z₀₁ = 0, z₀₂ = cos ω₀T, полюса: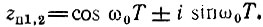

5. Последовательность выборок из сигнала s(t) = sin ω₀t, t ≥ 0. В этом случае 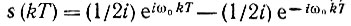и

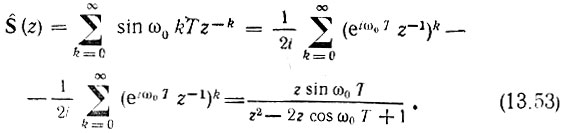
Нуль z₀ = 0, полюса: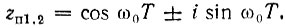

Положение нулей и полюсов для приведенных выше пяти сигналов показано на рис. 13.20.

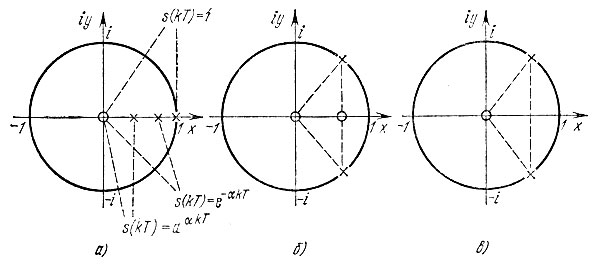
Рис. 13.20. Положение нулей и полюсов на z-плоскости для:

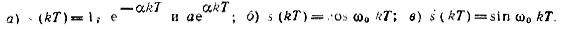
Отыскание оригинала, т. е. функции s_T(t), по заданному изображению Sˆ(z) производится с помощью обратного z-преобразования, которое получается подстановкой е^рТ = z в выражение (13.16).

С учетом соотношения 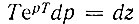это выражение приводится к виду

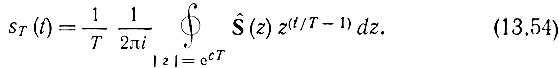
Интегрирование ведется по окружности радиуса r = е^сТ, в которую преобразуется прямая σ = с из плоскости р = σ + iω. Постоянная с определяется из условия, что все полюса подынтегральной функции находятся внутри круга радиуса r = е^сТ. Обход контура - в положительном направлении (против часовой стрелки). Изменению частоты от -∞ до ∞ соответствует бесконечное число обходов контура интегрирования.

По аналогии с выражением (13.19) значение импульса s(nТ) в точке t = nТ [без множителя δ(t - nТ)] можно определить с помощью более простого выражения

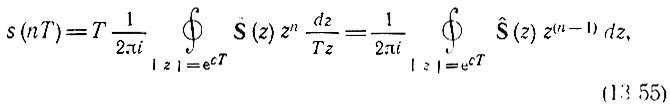
в котором подразумевается один обход контура интегрирования.

В рассмотренных выше примерах функций S(z), обладающих полюсами на окружности единичного радиуса [при s(kT) = 1, cos ω₀kT, sin ω₀kT], постоянная с > 0 может быть сколь угодно малой величиной. Поэтому контур интегрирования можно свести к окружности радиуса r = 1 с обходом полюсов вне круга, подобно тому, как на плоскости р = σ + iω интегрирование ведется по оси iω с обходом полюсов, лежащих на этой оси, справа.

С учетом этого условия, выражения (13.54), (13.55) в дальнейшем будем записывать в одной из двух форм:

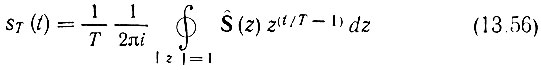
- с бесконечным числом обходов окружности единичного радиуса;

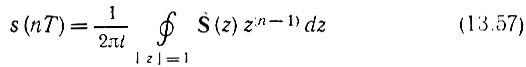
- с одним обходом окружности единичного радиуса.

Интегрирование по окружности r > 1 из дальнейшего рассмотрения исключается, поскольку положение полюсов функции S(z) вне круга r > 1 соответствует неограниченно возрастающим временным последовательностям, не имеющим физического смысла.

При применении выражения (13.56) следует учитывать полезное соотношение

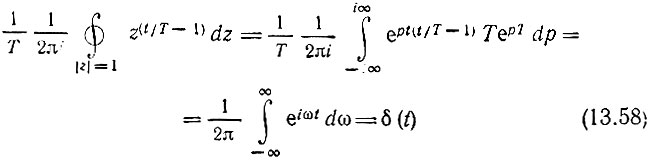
[см. выражение (3.17)].

Приведем в заключение двустороннее z-преобразование, получающееся подстановкой е^рT в (13.23):

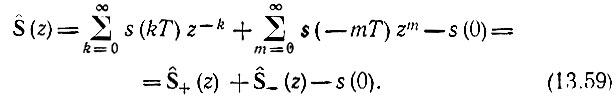
При четной функции s(t) второе слагаемое в правой части (13.59) можно привести к виду

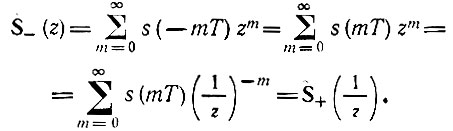
Таким образом, при четной функции s(t) выражение (13.59) переходит в

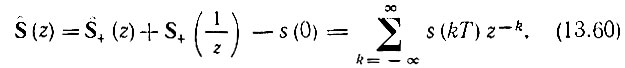
В этом выражении Sˆ+ обозначает одностороннее преобразование. Обратное z-преобразование производится с помощью выражений (13.56), (13.57).