13.10. Z-преобразование передаточных функций дискретных цепей

Применим z-преобразование к передаточной функции дискретной цепи. Подстановка е^рТ = z в выражение (13.40) дает

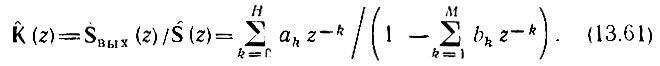
Из этого выражения видно, что передаточная функция дискретного фильтра является дробно-рациональной. По заданному выражению (13.61) легко составить уравнение вида (13.38), определяющее алгоритм преобразования входной импульсной последовательности в выходную. Для этого каждому из слагаемых вида s[(n - k)T] в уравнении (13.38) достаточно приписать коэффициент a_k при степени z^-k в числителе, а слагаемым вида s_вых[(n - k)T] коэффициент b_k при степени z^-k в знаменателе выражения (13.61).

Следует, однако, отметить, что не всякая дробно-рациональная функция может быть реализована в виде передаточной функции фильтра. Пусть, например, передаточная функция задана в виде отношения полиномов по положительным степеням

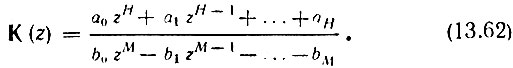
Разделив числитель и знаменатель на b₀z^M, приведем это выражение к виду

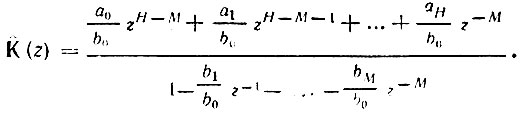
Если Н > М, то первое слагаемое в числителе (с положительной степенью z) образует в уравнении (13.38) слагаемое вида (a₀/b₀)s[(n + k)T], где k = -Н - М > 0, соответствует импульсу s(n + k), опережающему во времени входной импульс s(n), что, конечно, невозможно. Отсюда следует, что фильтр осуществим при условии, что степень знаменателя в (13.62) больше или равна степени числителя.

С учетом этих замечаний запишем передаточную функцию в следующих эквивалентных формах:

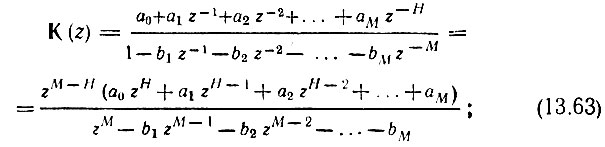
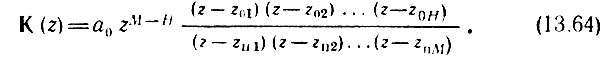
В выражении (13.63) коэффициенты a_k и b_k следует подставлять с теми же знаками, с которыми они входят в (13.38).

В выражении (13.64) z_0n - нули, а z_{п n} - полюса передаточной функции; z_0n и z_{п n} могут быть либо действительными, либо комплексными числами. В первом случае они расположены на действительной оси, а во втором образуют комплексно-сопряженные пары.

Нули могут быть расположены в любой точке плоскости z, полюса же - только внутри круга единичного радиуса. Это условие вытекает из требования устойчивости цепи; при рассмотрении поведения передаточной функции на плоскости р условие устойчивости требует расположения полюсов в левой полуплоскости. Как отмечалось выше, левая полуплоскость р отображается внутрь единичного круга на плоскости z.

Для перехода от функции 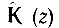к функции К_Т(iω) следует, как это вытекает из (13.46), приравнять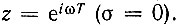

Таким образом,

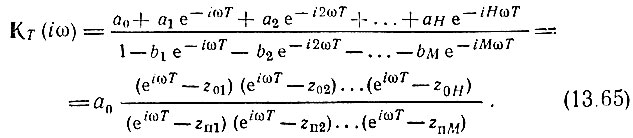
Для определения амплитудно-частотной характеристики цепи в диапазоне (0, 2π/Т) следует вычислить модуль выражения (13.65) при изменении ωТ от 0 до 2π, т. е. при одном обходе окружности единичного радиуса на z-плоскости. При последующих обходах окружности АЧХ периодически повторяется.

Модули разностей 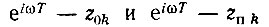являются расстояниями от точки на окружности, соответствующей углу ωТ, до нуля z_0k или полюса z_{п k}. Обозначив эти расстояния через R_0k и R_{п k}, получаем для АЧХ формулу

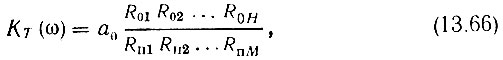
удобную для графических вычислений.

Вычисления особенно упрощаются при построении АЧХ в логарифмическом масштабе:

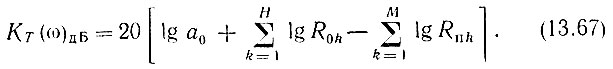
Если заданы нули и полюса передаточной функции, то коэффициенты a_k и b_k легко определяются с помощью известных из алгебры соотношений. Значительно более сложной (при М > 2) задачей является определение нулей и полюсов по заданным коэффициентам a_k и b_k.

Передаточная функция 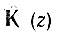и импульсная характеристика g_T(t) связаны между собой парой z-преобразований, вытекающих непосредственно из выражений (13.48) и (13.56), (13.57) при замене в первом из них s(kТ) на g(kT), а в (13.56), (13,57)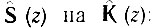

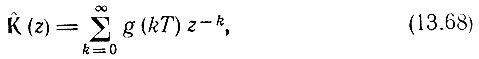
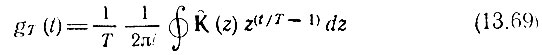
- бесконечное число обходов контура интегрирования,

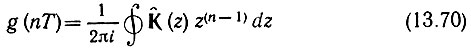
- один обход контура интегрирования.