13.11. Примеры анализа дискретных фильтров на основе метода z-преобразования

1. Нерекурсивный фильтр второго порядка

В соответствии с выражением (13.30) при Н = 2 передаточная функция фильтра, представленного на рис. 13.21, а, преобразуется в функцию

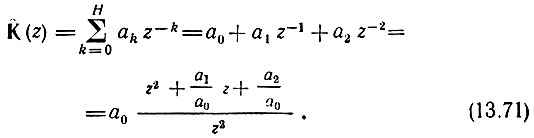
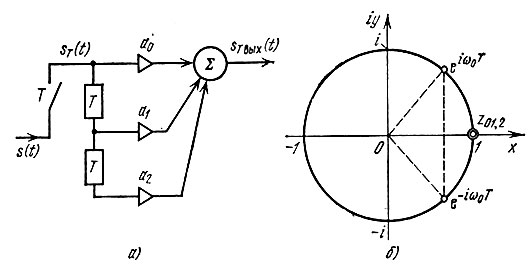
Рис. 3.21. Цифровой фильтр второго порядка (а) и положение нулей на z-плоскости (б)

Эта функция имеет нули в точках

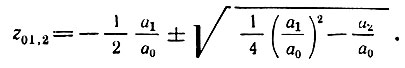
Двукратный полюс, расположенный в точке z_п = 0, не оказывает влияния на поведение передаточной функции.

Особый интерес представляют случаи 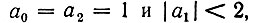когда

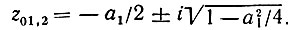
Модуль этого выражения равен единице, так что комплексно-сопряженные нули z₀₁ и z₀₂ лежат на окружности единичного радиуса. В частности, при а₁ = -2 двукратный нуль расположен в точке z = 1 (рис. 13.21, б). Этот случай соответствует широко распространенному в практике режекторному фильтру второго порядка с бесконечно большим затуханием на частоте ω = 0 (е^iωT = 1).

Амплитудно-частотную характеристику такого фильтра легко определить из выражения (13.71) при подстановке а₀ = а₂ = 1, 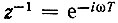и домножении правой части на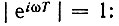

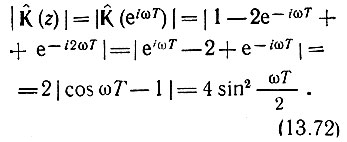
График этой функции представлен на рис. 13.22 (сплошная линия). Сопоставление (13.72) с выражением (13.35) показывает, что рассматриваемый фильтр второго порядка эквивалентен каскадному соединению двух фильтров первого порядка с коэффициентами а₀ = 1 и а₁ = -1.

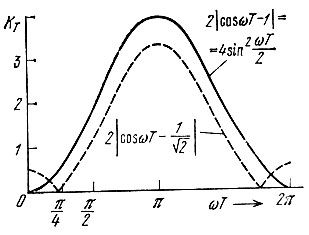
Рис. 13.22. Амплитудно-частотная характеристика фильтра (рис. 13.21, а) при а₀ = 1 и a₁ = -1

Изменением коэффициента ах можно перемещать нули z_01,2 по окружности единичного радиуса, что равносильно перемещению нуля АЧХ по оси частот. В частности, при 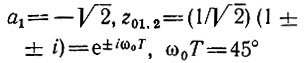(рис. 13.21, б). Соответствующая АЧХ изображена на рис. 13.22 (штриховая линия).

2. Рекурсивный фильтр первого порядка (рис. 13.15)

Передаточная функция (13.42) преобразуется к виду

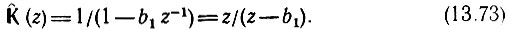
Эта функция имеет нуль в точке z₀ = 0 и полюс в точке z_п = b₁.

Определим импульсную характеристику фильтра с помощью формулы (13.69). Представив 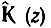в форме геометрической прогрессии

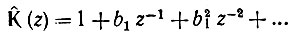
и применив к каждому слагаемому выражение (13.69), получим

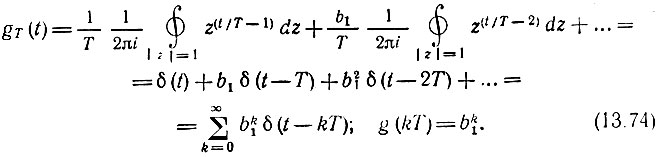
Из данного примера видно преимущество рекурсивного фильтра перед нерекурсивным. Для получения приведенной выше импульсной характеристики требуется всего лишь один элемент памяти Т, а в случае нерекурсивного - большое число (теоретически бесконечное). В рекурсивном фильтре это преимущество достигается благодаря циркуляции импульса по кольцу обратной связи с задержкой Т.

Представив b₁ в форме b₁ = е^-αT, запишем выражение (13.74) в виде

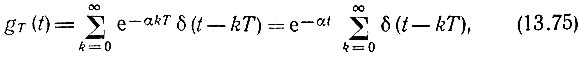
из которого следует, что дискретная импульсная характеристика рассматриваемой цепи совпадает с последовательностью выборок импульсной характеристики непрерывной RС-цепи, постоянная времени которой отвечает условию

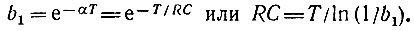
При этом, однако, амплитудно-частотные характеристики двух цепей существенно различны. Для дискретной цепи АЧХ определяется формулой (13.43), а для аналоговой цепи выражением

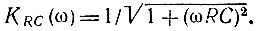
На рис. 13.23 сравниваются АЧХ К_дискр дискретной цепи (нормированной по максимальному значению) при b₁ = 0,2 с АЧХ K_RC [при RC = Т/ln(1/b₁)].

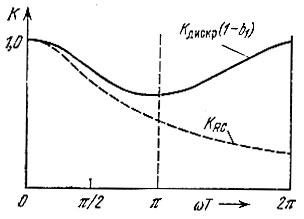
Рис. 13.23. Амплитудно-частотная характеристика цифрового фильтра (сплошная линия) и аналоговой RC-цепи (штриховая) при эквивалентности их импульсных характеристик

Деформация АЧХ дискретной цепи обусловлена гребенчатой структурой передаточной функции (см. § 13.5) и наложением хвостов АЧХ соседних частотных интервалов.

3. Рекурсивный фильтр второго порядка (рис. 13.24)

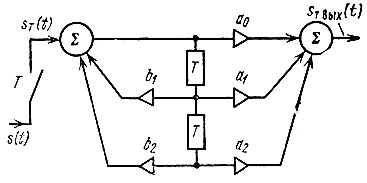
Рис. 13.24. Рекурсивный цифровой фильтр второго порядка

Передаточную функцию запишем сначала в форме

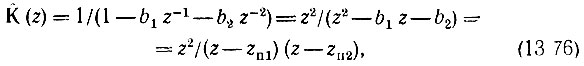
соответствующей случаю а₀ = 1, а₁ = 0, а₂ = 0, когда нули передаточной функции (в данном случае двукратный нуль) имеются только в точке z = 0, т. е. в центре окружности единичного радиуса.

Корни уравнения z₂ - b₁z - b₂ = 0 (полюса)

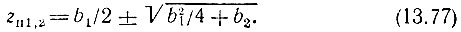
При b₂ < 0 и, кроме того, полюса z_п1 и z_п2 - комплексно-сопряженные числа:

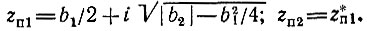
В этом случае

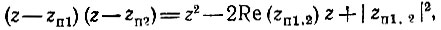
откуда вытекают следующие соотношения между коэффициентами полинома в (13.76) и полюсами z_{п 1,2}:

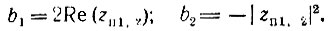
Представив z_{п 1,2} в форме

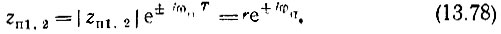
где r = |z_{п 1,2}| - расстояние полюса от начала координат, а φ_п = ω_пТ - азимут полюса (рис. 13.25), получим

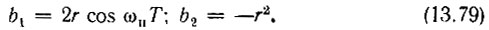
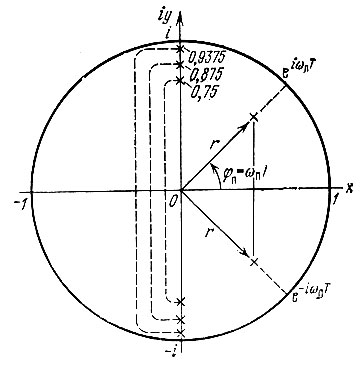
Рис. 13.25. Положение полюсов цифрового фильтра второго порядка на z-плоскости

Для определения АЧХ рассматриваемой цепи подставим в (13.76) z = e^iωT возьмем модуль

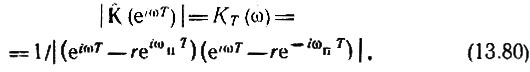
При заданном положении полюсов (т. е. при заданных r и ω_пТ) построение АЧХ удобно производить по формуле (13.66), измеряя R_п1 и R_п2 по чертежу. В данном случае с целью упрощения вычислений используем формулу (13.80) для частного случая ω_пТ = 90°. При этом выражение (13.80) легко приводится к виду

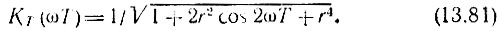
Графики функции К_Т(ωТ) для r = 0,75, 0,875 и 0,9375 представлены на рис. 13.26. С приближением r к единице рассматриваемая цепь приближается к резонатору с весьма высокой добротностью. При этом, однако, возникает опасность потери устойчивости.

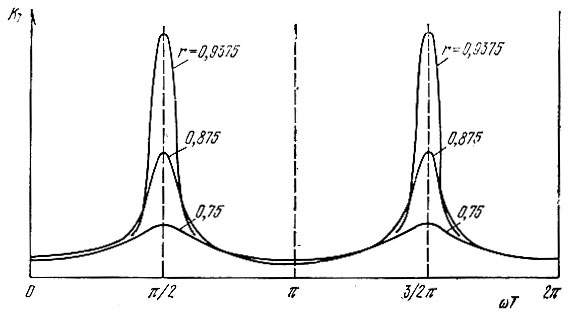
Рис. 13.26. Амплитудно-частотные характеристики рекурсивного фильтра второго порядка (см. рис. 13.24 и 13.25)

Рассмотрим теперь передаточную функцию второго порядка более общего вида, соответствующую схеме на рис. 13.24:

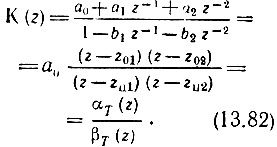
Как указывалось в § 13.6 [см. формулу (13.40) и пояснение к ней] фильтр с передаточной функцией (13.82) можно трактовать как каскадное соединение нерекурсивного фильтра [с передаточной функцией α_T(z)] и рекурсивного [с передаточной функцией 1/β_T(z)]. Такое сочетание можно использовать, в частности, в режекторном фильтре, рассмотренном в примере 1 и дополненном обратными связями для выравнивания АЧХ в полосе прозрачности фильтра.

На рис. 13.27 показан график функции |α_T(ω)|, перенесенный с рис. 13.22 (при а₀ = а₂ = 1, a₁ = -2), и график функции |1/β_T(ω)| при коэффициентах b₁ = 0,21875 и b₂ = 0,4375, а также результирующая АЧХ.

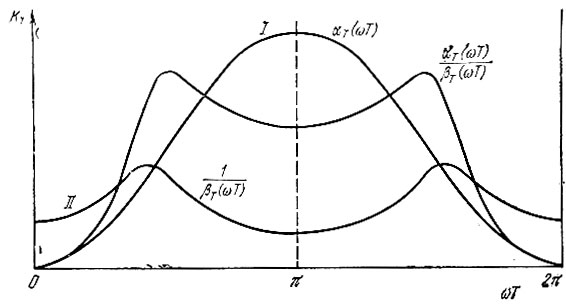
Рис. 13.27. Амплитудно-частотные характеристики рекурсивного звена с прямыми связями (I), звена с обратными связями (II) и цифрового фильтра в целом