13.12. Преобразование аналог - цифра. Шумы квантования

В предыдущих параграфах при изучении дискретных фильтров вопрос о неизбежной погрешности преобразования входного сигнала из аналоговой формы в цифровую не рассматривался. Погрешность возникает при квантовании сигнала на конечное, ограниченное число уровней. Чтобы выявить характер этой погрешности вернемся к структурной схеме цифровой обработки сигнала, представленной на рис. 13.1, и выделим из нее два устройства: преобразователь аналог - цифра (АЦП) и обратный преобразователь цифра - аналог (ЦАП).

Рассмотрим сначала совместную работу этих устройств без учета цифрового фильтра (рис. 13.1) при подаче на вход АЦП постоянного напряжения различного уровня u₁ (рис. 13.28, а). Основным параметром АЦП является число разрядов, используемых для кодирования входного напряжения. При двоичном коде число разрядов определяется числом двоичных элементов (например, триггеров), каждый из которых может находиться в одном из двух состояний: с нулевым или ненулевым напряжением на выходе. Одному из этих состояний условно приписывается нуль, а другому - единица. При числе двоичных элементов r на выходе АЦП получается комбинация (кодовое слово) из r символов, каждый из которых может принимать одно из двух значений (нуль или единица).

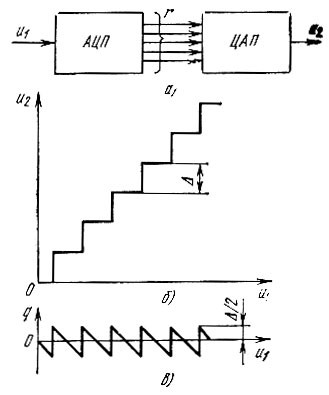
Рис. 13.28. Преобразование А/Ц и Ц/А (а), характеристика квантования (б) и ошибка квантования (в)

Как указывалось в § 13.1 число возможных различных комбинаций L = 2^r и определяет число дискретных уровней, на которое может быть разбит диапазон изменения входного напряжения u₁.

В ЦАП осуществляется обратное преобразование. Каждой комбинации нулей и единиц, поступающих на вход ЦАП, соответствует определенный дискретный уровень выходного напряжения. В результате при равномерном шаге квантования Δ зависимость u₂ от u₁ приобретает вид ломаной линии, показанной на рис. 13.28, б.

Устройство, представленное на рис. 13.28, а и обладающее подобной характеристикой, должно рассматриваться как нелинейное, а разность u₂ - u₁ = q - как ошибка, погрешность квантования. Видно, что наибольшая ошибка, по абсолютной величине не превышающая Δ/2, с возрастанием их остается неизменной (рис. 13.28, в).

Продолжим это рассмотрение для гармонического входного колебания s(t). Колебание s_вых(t) приобретает ступенчатую форму, отличающуюся от входного колебания s(t) (на рис. 13.29, б показанного тонкой линией), а ошибка квантования принимает вид функции

представленной на рис. 13.29, в.

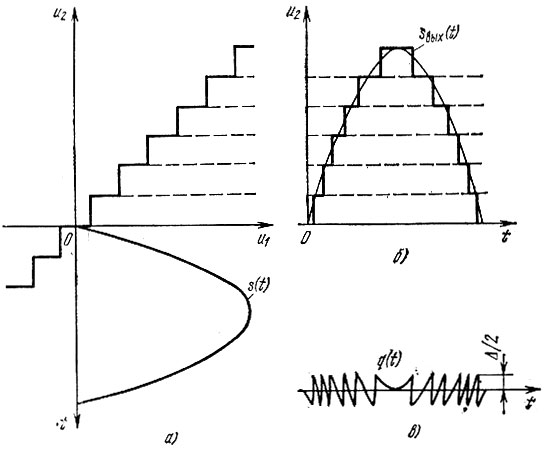
Рис. 13.29. Сигнал на входе (а) и выходе (б) квантующего устройства; помеха квантования (в)

При изменении в широких пределах амплитуды и частоты гармонического колебания s(t) изменяется только частота следования зубцов; форма их остается близкой к треугольной при неизменной амплитуде Δ/2. Функцию q(t) можно назвать помехой или шумом квантования. Нетрудно вычислить среднюю мощность шума квантования. При допущении треугольной формы зубцов (рис. 13.29, в) с амплитудой Δ/2 средняя за длительность одного зубца мощность равна ¹/₃ (Δ/2)² = Δ²/12. Так как эта величина не зависит от длительности зубца, можно считать, что средняя мощность шума квантования

Этот результат, выведенный для гармонического сигнала, можно распространить и на любой другой сигнал, в том числе и случайный. Отличие лишь в том, что функция q(t) будет случайным процессом из-за случайного характера длительности зубцов.

Нетрудно вычислить и отношение сигнал-помеха при квантовании. При высоте ступени Δ и общем числе ступеней, укладывающихся в пределах характеристики АЦП, равном L, амплитуда гармонического сигнала не должна превышать величины LΔ/2, а средняя мощность сигнала величины ¹/₂(LΔ/2)² (во избежание ограничения сигнала). Следовательно, отношение сигнал-помеха при квантовании гармонического колебания

Так как число уровней L связано с числом двоичных разрядов r соотношением L = 2^r, то выражение (13.85) можно представить в форме

Это соотношение можно рассматривать как частный случай общего выражения

где K_пф - пик-фактор сигнала, т. е. отношение максимального значения к среднеквадратическому.

При гармоническом колебании 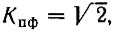что и приводит к выражению (13.86); при случайном сигнале с нормальным законом распределения K_пф может быть принят 2,5-3 (см. § 4.2, п. 4); в этом случае P_sP_q ≈ 2^2r/3, а среднеквадратическое напряжение сигнала не должно превышать ~LΔ/6. Физический смысл выражения (13.87) очевиден: с увеличением числа разрядов r очень быстро возрастает число дискретных уровней, приходящихся на заданный диапазон изменения s(t), и, следовательно, снижается перепад Δ двух соседних уровней.

При грубой оценке превышения сигнала над шумом квантования исходят из соотношения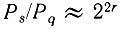

или в децибелах

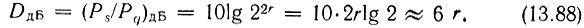
В современных АЦП число разрядов достигает десяти и более. При этом величина D_дБ, характеризующая динамический диапазон АЦП, составляет ~60 дБ (6 децибел на один разряд)^*.

^* (При пик-факторе K_пф ≈ 3 [см. формулу (13.87)] величина D_дБ уменьшается до 5,5 дБ на один разряд.)

Другой важной характеристикой шума квантования является его спектральная характеристика. При гармоническом колебании помеха является периодической функцией времени. Спектр ее, как и при любом другом нелинейном преобразовании, является линейчатым, содержащим только частоты, кратные частоте входного колебания. Из-за зубчатой формы функции q(t) (рис. 13.29, в) спектр шума богат высшими гармониками.

При входном воздействии типа случайного процесса с дисперсией σ²_s и со среднеквадратической шириной энергетического спектра f_{s ск} статистические характеристики шума квантования зависят не только от характеристик исходного процесса s(t), но в сильной степени и от соотношения между σ_s и Δ. В частности, при 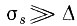ширина f_{q ск} энергетического спектра шума квантования W_q(ω) во много раз больше ширины f_{s ск} спектра процесса s(t).

Введем в рассмотрение дискретизацию входного сигнала по времени. На рис. 13.30 представлены одна из реализаций случайного сигнала s(t) и совокупность выборок, взятых с шагом Т.

В АЦП каждая из выборок преобразуется в цифровой код, как это было описано в § 13.1 и в начале данного параграфа для постоянного напряжения.

Как это очевидно из предыдущих рассуждений, преобразование осуществляется с ошибкой, заключенной в пределах 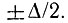Если выборки берутся из случайного сигнала, а изменение функции s(t) за время Т превышает Δ или тем более несколько Δ, то ошибки в различные отсчетные моменты времени nТ и (n + 1)Т можно считать взаимно независимыми и равновероятными. Дисперсия случайной величины q, равновероятной в интервале (-Δ/2, Δ/2), равна (1/3)(Δ/2)² (см. § 4.2, п.1). Этот результат совпадает с выражением (13.84), полученным усреднением мощности шума квантования по времени. Сделанные выше допущения равносильны утверждению, что дискретная последовательность ошибок q(nТ) соответствует выборкам из некоррелированного шума, т. е. шума с равномерным энергетическим спектром. Этот спектр, как отмечалось выше, во много раз шире спектра исходного случайного процесса s(t). В связи с этим шум квантования обычно рассматривают как белый шум, аддитивный по отношению к s(t). Так как процесс квантования осуществляется на входе цифрового фильтра, то шум квантования можно трактовать как собственный шум цифрового фильтра (отнесенный к его входу).

Определим энергетический спектр шума квантования. Пусть полная ширина спектра шума квантования в отсутствие временной дискретизации равна f_{q ск}. При дискретизации шума квантования с шагом Т = 1/f₁ результирующий спектр является суммой парциальных спектров, сдвинутых один относительно другого на величину ω₁ = 2π/Т (см. § 13.3, рис. 13.6). Особенностью рассматриваемого случая является то, что 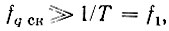так что имеет место многократное перекрытие спектров.

В пределах частотного интервала (0, f₁) каждый отдельный спектр содержит мощность (Δ²/12)f₁/f_{q ск}. Но и число перекрывающихся спектров равно f_{q ск}/f₁. Поэтому результирующая мощность шума квантования в полосе (0, f₁) будет Δ²/12. Можно поэтому считать, что в указанном частотном интервале энергетический спектр равномерен (белый шум) и равен

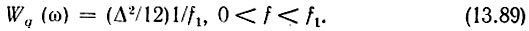
При амплитудно-частотной характеристике цифрового фильтра K²_T(ω) энергетический спектр шума квантования на выходе фильтра

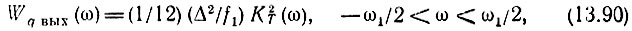
а средняя мощность (дисперсия)

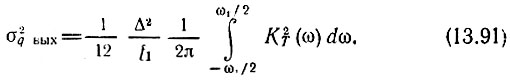
Для иллюстрации количественной стороны вопроса определим основные параметры шума квантования на выходе режекторного фильтра второго порядка, рассмотренного в примере I, § 13.11, при следующих данных:

- число разрядов квантования r = 8;

- раствор характеристики АЦП 10 В;

- шаг дискретизации Т = 1/f₁ = 1 мс; f₁ = 1000 Гц.

Шаг квантования Δ найдем, разделив 10 В на число уровней:

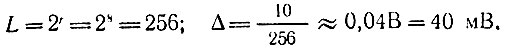
Дисперсия шума на входе

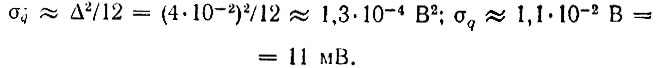
Основываясь на 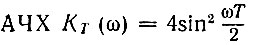[см. формулу (13.72)], находим

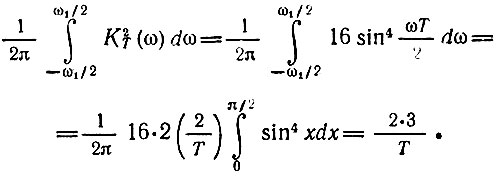
Применяя формулу (13.91), получаем

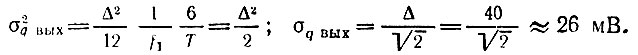
Итак, уровень собственных шумов квантования на выходе рассматриваемого фильтра равен 26 мВ.

Энергетический спектр этого шума повторяет форму квадрата АЧХ:

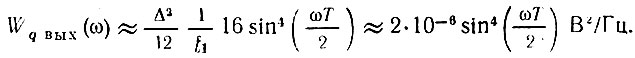
В заключение укажем на требования, предъявляемые к АЦП в зависимости от скорости изменения входного сигнала s(t). Длительность выборки τ_в задается настолько короткой, чтобы изменение s(t) за время τ_в было пренебрежимо мало. Во всяком случае, это изменение должно быть меньше Δ. В современных АЦП τ_в снижают до единиц наносекунд.

В § 13.1 указывалось, что электронный ключ, с помощью которого берутся из сигнала s(t) выборки, снабжается RС-цепью для запоминания уровня выборки на время, необходимое для срабатывания АЦП. В быстродействующих АЦП это время составляет десятки наносекунд.