13.13. Преобразование цифра - аналог и восстановление континуального сигнала

Обратное преобразование сигнала из цифровой в континуальную форму^* производится с помощью двух устройств: а) преобразователя цифра - аналог (ЦАП), б) синтезирующего фильтра (см. схему на рис. 13.1).

^* (В ряде применений цифровой фильтрации не требуется обратного перехода от цифрового сигнала к аналоговому. Так, например, в радиолокационных системах с цифровой обработкой сигнала последний вводится в ЭВМ непосредственно в цифровой форме.)

В ЦАП имеется набор фиксированных напряжений, соответствующих каждому из r разрядов, и устройство для синхронного подключения (или отключения) этих напряжений к сумматору в зависимости от поступающих из АЦП символов (имеется в виду схема на рис. 13.28, а). Максимальное напряжение на выходе ЦАП получается, когда со всех элементов поступают единицы. Пусть, например, число разрядов r равно четырем и, следовательно число дискретных уровней L равно 2⁴ = 16, а максимальное напряжение сигнала условно равно 1 В. Тогда цена самого младшего разряда 1/16 В, следующего за ним 1/8 В, затем 1/4 В и 1/2 В. При кодовом слове, поступающем от АЦП в виде 0,1111, напряжение на выходе ЦАП будет 1/2 + 1/4 + 1/8 + 1/16 = 15/16. В (максимальное значение), а при коде 0,0001 - 1/16 В (минимальное значение). Кодовому слову 0,0010 соответствует напряжение 2/16 В, слову 0,100 - 1/2 В и т. д.

Указанные напряжения поддерживаются на выходе ЦАП в течение времени τ₀ < T, а в некоторых системах вплоть до поступления новой кодовой группы (τ₀ = Т). В результате напряжение на выходе ЦАП при фильтрации сигнала s(t) приобретает характер импульсной последовательности, представленной на рис. 13.31 (при τ₀ < Т). Амплитуды прямоугольных импульсов равны соответствующим отсчетам, поступающим (в закодированном виде) от АЦП.

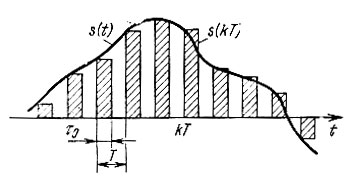
Рис. 13.31. Выборки в виде прямоугольных импульсов

Спектр такой последовательности имеет сложную структуру. Фильтр на выходе ЦАП с полосой пропускания меньшей или равной частоте f₁/2, где f₁ = 1 /Т - частота повторения импульсов, выделяет основной частотный интервал, в котором содержится вся информация о сигнале s(t) (спектр которого должен быть не шире f_m = f₁/2). На этом и заканчивается процедура восстановления континуальной формы профильтрованного сигнала. Следует, однако, иметь в виду, что спектр последовательности "толстых" импульсов: показанных на рис. 13.31, может существенно отличаться от спектра, найденного в § 13.3 для тонких импульсов (теоретически δ-функций).

В данном случае нельзя импульсную последовательность (рис. 13.31) трактовать просто как произведение континуального сигнала s(t) на тактовую последовательность прямоугольных импульсов. Каждый из прямоугольных импульсов с амплитудой s(kT) можно представить в виде свертки прямоугольного импульса υ₀(t), показанного на рис. 13.32, с функцией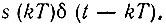

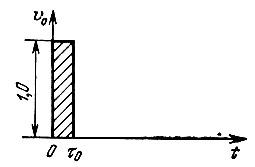
Рис. 13.32. Тактовый импульс

Действительно,

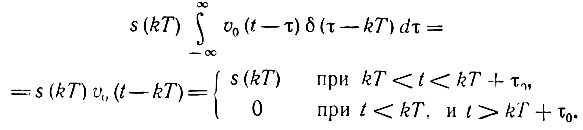
Таким образом, всю последовательность импульсов на выходе ЦАП (в отсутствие ЦФ, при схеме, показанной на рис. 13.28, а) можно записать в виде

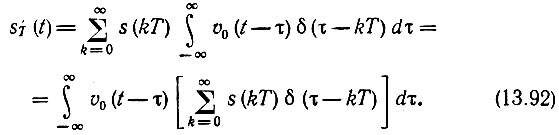
Получилась свертка двух функций: υ₀(t) и 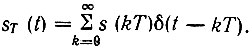Первой соответствует спектральная плотность [см. (2.67) и рис. 2.15]

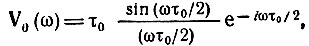
а функции 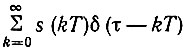- спектральная плотность [см. (13.10)]

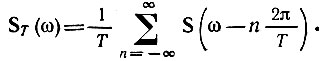
Следовательно, временной свертке (13.92) соответствует спектральная плотность, равная произведению [см. (2.64)]:

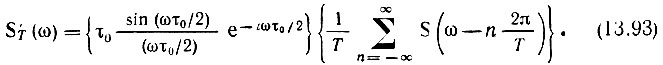
График модуля функции S'_T(ω) для двух значений τ₀ < Т и τ₀ = Т представлен на рис. 13.33. Штриховыми линиями показаны истинные спектры сигнала s(t), которые получились бы при тонких выборках.

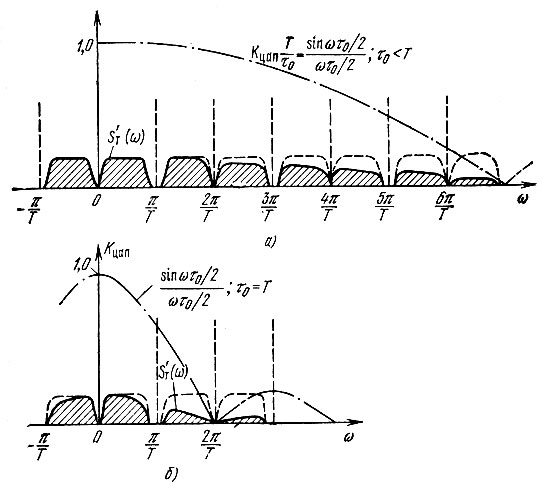
Рис. 13.33. Амплитудно-частотная характеристика ЦАП и спектральная плотность сигнала на его выходе: а - при тонких; б - при толстых выборках

Видно, что утолщение импульсов приводит к деформации спектра передаваемого сигнала, причем эта деформация выражена сильнее для высших частот сигнала.

Множитель

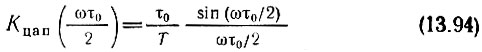
в выражении (13.93) можно рассматривать как амплитудно-частотную характеристику преобразователя цифра - аналог (НА рис. 13.33 функция K_ЦАП/(τ₀/T) показана штрих-пунктиром).

Остановимся в заключение на требованиях к амплитудно-частотной характеристике синтезирующего фильтра К_ф(ω). Идеальная характеристика должна иметь вид, показанный на рис. 13.34 сплошной линией. Если спектр полезного сигнала значительно уже частотного интервала (-f₁/2, f₁/2), то требования к крутизне скатов характеристики могут быть ослаблены (см. штриховую линию на рис. 13.34).

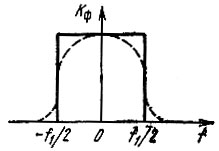
Рис. 13.34. Амплитудно-частотная характеристика синтезирующего фильтра идеального (сплошная линия) и реального (штриховая)