13.14. Быстродействие арифметического устройства цифрового фильтра. Шумы округления

Структурная схема любого цифрового фильтра содержит элементы памяти Т, сумматоры и перемножители. Совокупность этих элементов образует арифметическое устройство фильтра. (Коммутирующие устройства, необходимые для синхронной записи и считывания двоичных символов в элементах памяти, и другие вспомогательные цепи здесь не рассматриваются.)

Элементы памяти Т представляют собой набор двоичных элементов, число которых равно числу разрядов r.

Перемножители, реализующие весовые коэффициенты а₀, а₁, а₂, ... и b₁, b₂, ... работают по принципу поразрядного перемножения всех разрядов входного числа на каждый из разрядов числа, представляющего весовой коэффициент, и последующего суммирования частных произведений. Число двоичных разрядов r_{а, b}, используемых для представления весового коэффициента, зависит от требуемой точности вычислений. В больших ЭВМ r_{а, b} достигает 16 и более разрядов, в цифровых фильтрах часто можно ограничиваться 4-6 разрядами. Для полного сохранения информации, содержащейся во входном сигнале s(t), число разрядов произведения должно равняться сумме r + r_{а, b}. На это число разрядов должны быть рассчитаны все последующие элементы цифрового тракта. Для сокращения объема аппаратуры обычно идут на округление произведения путем отсекания младших разрядов. Это приводит к ошибке, которую называют шумом округления.

Статистические свойства шума округления в основном совпадают с шумом квантования; дисперсия шума округления приравнивается величине Δ²_{а, b}/12, где Δ_{а, b} - перепад уровней, соответствующий отбрасываемому разряду произведения.

Одной из важнейших характеристик арифметического устройства ЦФ является его быстродействие, определяемое числом операций, которое необходимо произвести за время Т, и длительностью одной операции. Последняя не может быть меньше, чем время срабатывания двоичных элементов (триггеров). Быстрое и непрерывное развитие микроэлектронной техники с каждым годом сокращает инерционность электронных приборов, используемых в вычислительной технике. В современных приборах время срабатывания составляет единицы наносекунд.

Определим число операций, которое необходимо совершить за время Т при обработке сигнала по заданному алгоритму.

В качестве исходного алгоритма возьмем свертку, определяемую выражением (13.7). Из этого выражения видно, что для определения одной n-й выборки выходного сигнала требуется совершить n операций перемножения и столько же операций сложения. При числе выборок в обрабатываемой реализации сигнала 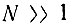общее число операций умножения равно 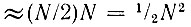(столько же операций сложения).

Как уже упоминалось выше, операция умножения осуществляется многократным сложением, причем число элементарных сложений определяется числом разрядов сомножителей. При длительности одной операции сложения τ₁ и числе разрядов r общая длительность обработки N выборок T_обр = (N²)rτ₁. В тех случаях, когда требуется обработка "в реальном времени", т. е. по ходу поступления сигнала s(t), Т_обр не должно превышать длительности обрабатываемой реализации Т_с = NT. Отсюда получается условие

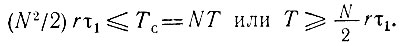
Подставляя в это неравенство 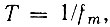приходим к следующей грубой оценке наивысшей допустимой частоты сигнала:

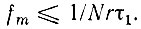
В частности, при N = 1000, r = 10 и τ₁ = 1 нс,

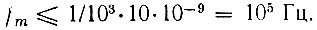
При обработке более коротких сигналов, например с базой N = 50, частота может быть доведена до 2 МГц.

Как видим, применение цифровых фильтров, работающих в режиме последовательного анализа, ограничивается в настоящее время относительно низкочастотными сигналами.

При переходе к параллельному анализу с помощью нескольких каналов ценой усложнения и удорожания аппаратуры быстродействие можно существенно повысить.

В принципе, быстродействие можно довести до величины, близкой к τ₁, т. е. f_m ≤ 1/τ₁.

Главной особенностью цифрового фильтра является то, что его характеристики - амплитудно-частотная и фазочастотная - определяются всего лишь весовыми коэффициентами в прямых и обратных связях и шагом дискретизации Т. Это позволяет строить фильтры с характеристиками, реализация которых с помощью обычных фильтров на индуктивностях и емкостях весьма затруднительна или даже вовсе невозможна.

Применением кварцованных источников колебания тактовой частоты можно обеспечить очень высокую стабильность частотных характеристик. Цифровые фильтры надежны в работе, не требуют подстройки и нечувствительны к температурным и иным условиям эксплуатации.

Простота осуществления устройств памяти при использовании цифровых сигналов делает цифровые фильтры незаменимыми при обработке, требующей задержку сигнала во времени. Наконец, следует отметить удобство сопряжения цифровых фильтров с ЭВМ.

Благодаря всем этим преимуществам цифровые фильтры, несмотря на сложность построения их схемы и необходимость синхронизации управления электронными ключами, находят все большее распространение в практике.