Глава 14. Представление колебаний некоторыми специальными функциями

14.1. Введение

В § 2.2 отмечалось, что в тех случаях, когда требуется аппроксимировать заданную функцию f(х) с помощью ограниченного числа членов ряда, применяются различные ортогональные системы специальных, не гармонических функций. Условия ортонормированности этих функций на заданном интервале (а, b) записываются в форме

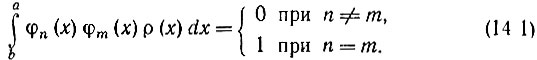
От определения (2.3) это выражение отличается множителем ρ(х) под знаком интеграла, называемым весовой функцией или функцией веса. Говорят, что функции φ_n(х) и φ_m(х) ортогональны с весом ρ(х). Это означает, что ортогональны не эти функции, а функции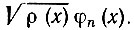

При определении коэффициентов обобщенного ряда Фурье, аппроксимирующего функцию f(х), следует исходить из формулы, аналогичной (2.9), но с учетом весовой функции ρ(х):

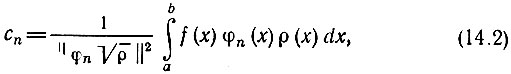
где

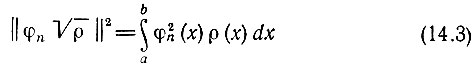
- квадрат нормы функции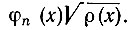

Для представления непрерывных сигналов наиболее употребительны ортогональные полиномы и функции Лежандра, Чебышева, Лагерра, Эрмита и т. д., которым посвящены § 14.2, 14.3. Для представления дискретных сигналов широкое распространение получили кусочно-постоянные функции Хаара, Радемахера и Уолша. Функции Уолша, хорошо сочетающиеся с требованиями вычислительной техники, а также микроэлектроники, приобрели особо важное значение. Рассмотрению свойств непрерывных функций Уолша посвящены § 14.4-14.6, а дискретных функций Уолша - § 14.7.